Solutions of Implication Constraints yield Type Inference for More General Algebraic Data Types
|
|
|
- Angel Adams
- 5 years ago
- Views:
Transcription
1 Solutions of Implication Constraints yield Type Inference for More General Algebraic Data Types Peter J. Stuckey NICTA Victoria Laboratory Department of Computer Science and Software Engineering The University of Melbourne, Vic. 3010, Australia Ô ºÑÙºÓÞº Ù Martin Sulzmann School of Computing, National University of Singapore S16 Level 5, 3 Science Drive 2, Singapore ÙÐÞÑ ÒÒÓÑÔºÒÙ º Ùº Abstract We study an extension of Hindley/Milner with a user-programmable constraint domain and a general form of algebraic data types which unifies common forms such as existential types, the combination of type classes and existential types and the more recent extension of guarded recursive data types. We can furthermore express some novel variants such as a limited form of dependent types. Type inference is reduced to solving of implication constraints. We identify sufficient conditions in terms of solutions of implication constraints under which inference is sound and complete. One of our main technical achievements is a generic implication solver which is parameterized in the solver of the underlying constraint domain. Our results show that our system is practical and greatly extends the expressive power of languages such as Haskell. 1. Introduction The concept of algebraic data types allows to write functions which pattern match over user-definable types. Such a feature is highly desired by programmers and supported by a number of languages, e.g. consider Haskell [7] and ML [21]. There exist several extensions of algebraic data types which allow to increase the expressiveness of the language significantly. E.g., Läufer and Odersky [18] consider the addition of existential types whereas Läufer [17] was the first to introduce a combination of type classes [34] and existential types [18]. Note that Läufer only gives a formal account for single-parameter type classes. However, some implementations, e.g. GHC [5] and Hugs [10], also support more advanced type class extensions such as constructor classes [12], multi-parameter type classes [14] and functional dependencies [13]. To the best of our knowledge, there does not exist any formal description of the combination of these type class extensions and existential types. More recently, Xi, Chen and Chen [35] introduced yet another extension of algebraic data types known as guarded recursive data types. All these extensions are very interesting but have largely been studied independently. This paper attempts to unify these seemingly unrelated extensions. Our contributions are: Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. To copy otherwise, to republish, to post on servers or to redistribute to lists, requires prior specific permission and/or a fee. Copyright c ACM [to be supplied]... $ /4/13
2 We present an extension of Hindley/Milner with a user-programmable constraint domain and a general form of algebraic data type (Section 3). Among others we can support type classes and existential types, guarded recursive data types and some other novel variants of algebraic data types. We introduce an algorithm Ï style inference system where the program text generates implication constraints (compare this to standard Hindley/Milner where we only generate sets of primitive constraints such as equations etc). We give a general characterization of solutions for implication constraints. Thus, valid solutions yield sound inference and principal solutions yield principal types (Section 4) We define a generic solver for implication constraints which is parameterized in terms of a solver for sets of primitive constraints. Hence, we can support type inference for all instances of our framework. For the important case of multi-parameter type classes with existential types we identify sufficient conditions under which we can compute principal solutions (Section 5). Our system has been implemented as part of the Chameleon system [32] (experimental version of Haskell). Thus, we can greatly extend the expressive power of languages such as Haskell. In the following section we give an overview of our work by briefly reviewing previous extensions of algebraic data types. We also sketch some novel extensions now possible. Furthermore, we motivate how to attack the challenging type inference problem. Related work is discussed in Section 6. We conclude in Section 7. Section 2 introduces some basic notations and makes some silent assumptions explicit. 1.1 Overview We start off by considering some classical examples of existing variants of algebraic data types. Note that we use Haskell-style syntax throughout. EXAMPLE 1. The following program makes use of existential types as introduced by Läufer and Odersky [18]. Ø Ã ÓÖ ÐÐ º Å ¹ ÁÒص Å Ü µ Ü The algebraic data type à has one constructor Å of type ÁÒص Ã. Note that variable does not appear in the result type. In the Haskell syntax we indicate this explicitly via ÓÖ ÐÐ. When constructing a value of type à we are able hide the actual values involved. Effectively, refers to an existentially bound variable. Thus, when pattern matching over à values we should not make any assumptions about the actual values involved. This is the case for the above program text. We find that the type of is à ÁÒØ. The situation is different in case of ½ Å Ü µ Ü Üµ The type of Ü escapes as part of the result type. However, we have no knowledge about the actual type of Ü. Hence, function ½ should be rejected. In some subsequent work, Läufer [17] considers a combination of single-parameter type classes [34] and existential types. EXAMPLE 2. Consider Ð Ã Ý Û Ö ØÃ Ý ¹ ÁÒØ Ø Ã ÓÖ ÐÐ º Ã Ý Å Å Üµ ØÃ Ý Ü The class declaration introduces a single-parameter type class à Ý. In type schemes, bound type variables may be constrained by type classes. We have the following primitive functions ØÃ Ý Ã Ý µ ÁÒØ and Å Ã Ý µ Ã. The program text ØÃ Ý Ü gives rise to Ã Ý where is an existentially bound variable. Note that Ã Ý is provided by the constructor. Hence, function is of type à ÁÒØ /4/13
3 Guarded recursive data types [35] (GRDTs) introduced by Xi, Chen and Chen are one of the latest extensions of the concept of algebraic data types. They are similar to Läufer s system [17] in that both are extensions of existential types. The novelty of GRDTs is that we may make use of additional type equality assumptions while typing the body of a pattern clause. A number of authors [24, 1, 23] have shown that such an extension is highly useful. EXAMPLE 3. Here, we give excerpts of a standard program which defines an evaluator for a simple term language. Ø Ì ÖÑ ÁÒص Á ÖÓ ÓÖ ÐÐ º µµ ººº Ú Ð Ì ÖÑ ¹ Ú Ð Á ÖÓ ¼ È Ö Ì ÖÑ µ Ì ÖÑ µ Ú Ð È Ö Ø½ ص Ú Ð Ø½ Ú Ð Øµ ººº The type equalities attached to constructors essentially mimic the typing rules of a simply-typed language. We make use of these constraints when typing functions which pattern match over GRDTs. E.g. in case of the second function clause we temporarily make use of µ. We find that the program text Ú Ð Ø½ Ú Ð Øµ has type µ which is equivalent to. Hence, the type annotation is correct. We observe that typing-wise the differences between GRDTs and Läufer s type classes with existential types are marginal. Both systems make temporary use of primitive constraints (either type equalities or type class constraints) while typing the body of a pattern clause. E.g, in Example 2 we temporarily make use of Ã Ý arising out of pattern Å Ü and in Example 3 we temporarily make use of µ arising out of pattern È Ö Ø½ Ø. As we will see, both are natural instances of our framework. In our system, we can define even more general algebraic data types thanks to our user-programmable constraint domain. We make use of Constraint Handling Rules (CHRs) [3] which define incremental constraint solvers in terms of rewrite relations among constraints. Note that CHRs serve as a low-level notation for type classes [27, 4]. Thus, we can define data types which combine the ideas of GRDTs and Läufer style type classes with existential types. In the following example we show how to model a limited form of dependent types in style of Zenger s index types [36] where lists are indexed by their length. EXAMPLE 4. The following CHRs describe (directed) addition on the level of types. We assume that is a ternary constraint symbol, ÖÓ is a constant and ËÙ is a unary type constructor allowing us to represent natural numbers. (A1) ÖÓ Ñ Ñ µ Ì ÖÙ (A2) Ë٠е Ñ ËÙ Òµ µ Ð Ñ Ò (A3) Ð Ñ Ò ½ Ð Ñ Ò µ Ò ½ Ò (A4) ÖÓ Ñ Ò µ Ñ Ò (A5) Ë٠е Ñ Ò ¼ µ Ò ¼ ËÙ Ò Operationally, propagation rules ( µ) add constraints whereas simplification rules ( µ) replace constraints by some other constraints. Logically, µ can be interpreted as Boolean implication and µ as Boolean equivalence. E.g., rules (A1-2) define inductively addition among our representation of natural numbers and rules (A3-5) state that the first two (input) parameters functionally define the third (output) parameter. We could also make use of additional CHRs such as ÖÓ ÁÒØ ÁÒØ µ Ð to rule out certain invalid instances, thus ensuring that type parameters of are only of the form ÖÓ or ËÙ Ü /4/13
4 We make use of the above CHRs to give a refined definition of lists. ¹¹ ØÝÔ Ò Ü Ø ØÝÔ Ø Ä Ø Ò Ò ÖÓ Æ Ð ÓÖ ÐРѺ ËÙ ÖÓµ Ñ Ò ÓÒ Ä Ø Ñµ The second type parameter keeps track of the length of the list. The observant reader will notice that we could equivalently replace ËÙ ÖÓµ Ñ Ò by Ò ËÙ Ñ in the definition of Ä Ø Ò. However, there are clearly other examples which benefit from constraining the output types of constructor not only by equations but also by user-defined constraints The user-defined constraint is crucial to state that appending two lists of length Ð and Ñ yields a list whose length is the sum of Ð and Ñ. The following type checks in our system. ÔÔ Ò Ð Ñ Ò ÔÔ Ò Æ Ð Ý Æ Ð Ä Ø Ð ¹ Ä Ø Ñ ¹ Ä Ø Ò ÔÔ Ò ÓÒ Ü Ü µ Ý ÓÒ Ü ÔÔ Ò Ü Ý µ To verify type correctness of both clauses it is important to take into account the specific type information arising out of patterns. E.g., we type the first clause under the additional assumption Ð ÖÓ. Then, constraint ÖÓ Ñ Ò implies Ò Ñ under the CHR (A4). Hence, the first clause is type correct (which has type Ä Ø ÖÓ Ä Ø Ñ Ä Ø Ñ and this type is equivalent to Ä Ø Ð Ä Ø Ñ Ä Ø Ò under the temporary constraints Ð ÖÓ and Ò Ñ). We conclude that in our system the types of constructors of data types may be constrained by arbitrary constraints whose meaning is defined in terms of CHRs. We may temporarily make use of these constraints while typing pattern clauses. Thus, we can combine a number systems which previously required some specialpurpose type systems. The formal underpinnings of our system are described in Section 3. To be of practical use we will need to ensure that type inference for our system remains tractable. The common route towards type inference is to generate an appropriate constraint out of the program text and then solve this constraint. E.g., in case of standard Hindley/Milner we generate conjunctions of type equalities which can then be solved by a unification procedure. Principal solutions, i.e. most general unifiers, exists and therefore standard Hindley/Milner enjoys principal types [2]. The challenge here is that we will need implication constraints of the form ½ µ to represent the typing problem. Symbol denotes Boolean implication, constraints ½ and are conjunctions of primitive constraints and is again a conjunction of implication constraints. The need for such implication constraints should be clear given that we may type check programs under some temporary assumptions arising out of patterns. We could trivially achieve type inference by taking such implication constraints as the final result. This has the unpleasant effect that types become unreadable and inference intractable. Note that we still need to check that the final result is satisfiable. Depending on the primitive constraint domain satisfiability checking for implication constraints amounts to full-blown theorem proving. The path we choose is less ambitious in the sense that we restrict the set of allowable constraints to appear in the type system (i.e. in the constraint component of types and typing judgments). Our assumption is that only conjunction of primitive constraints are allowed to appear. The challenge we face is that implications constraints need to be solved and not only checked for satisfiability. One of our major technical contributions is a novel implication solver which is parameterized in terms of the underlying CHR solver. Thus, we can support type inference for all instances of our system. We have implemented a tractable version of our solver as part of the Chameleon system [32] which we believe improves over GHC [5]. For the important case of multi-parameter type classes with existential types we can identify sufficient conditions under which we find principal solutions, i.e. achieve principal types /4/13
5 In general, our system is incomplete. That is, we cannot guarantee principal types and therefore inference may fail. The reason is that implication constraints may have incomparable solutions. There is no way out here unless we allow for more expressive types. But we ruled out this path, see above. Another solution seems to make inference more predictable (a.k.a. well-behaved). The trouble is that inference will never be predictable due to unavoidable type errors. Another objection against well-behaved inference is that we may reject some reasonable programs. Therefore, we accept the fact that our inference system is incomplete in general. The significant advantage of our approach is that we can naturally support the type error reporting methods developed in [30, 29]. In our opinion, it is much more important to assist the user in case of type inference failure than being able to claim that inference is complete. Details of type inference and our implication solver can be found in Sections 4 and Preliminaries We write Ó to denote a sequence of objects Ó ½,...,Ó Ò. As it is common, we write to denote an environment consisting of a sequence of type assignments Ü ½ ½ Ü Ò Ò. Types will be defined later. We commonly treat as a set. For brevity, we write Ü µ to denote Ü. We write - to denote set subtraction. We write fv Óµ to denote the set of free variables in some object Ó with the exception that fv Ü ½ ½ Ü Ò Ò µ denotes fv ½ Ò µ. In case objects have binders, e.g., we assume that fv Óµ fv Óµ where is a fresh variable and a renaming. We generally assume that the reader is familiar with the concepts of substitutions, unifiers, most general unifiers (m.g.u.) etc [16] and first-order logic [25]. We use common notation for Boolean conjunction ( ), implication ( ) and universal ( ) and existential quantifiers ( ). Often, we abbreviate by, and use set notation for conjunction of formulae. We sometimes use Î ÑÐ as a short-hand for fv ÑÐ µ Î ÑÐ where Fml is some first-order formula and Î a set of variables, that is existential quantification of all variables in Fml apart from Î. We write to denote the model-theoretic entailment relation. When writing logical statements we often leave (outermost) quantifiers implicit. E.g., let ÑÐ ½ and ÑÐ be two formulae where ÑÐ ½ is closed (contains no free variables). Then, ÑÐ ½ ÑÐ is a short-hand for ÑÐ ½ fv ÑÐ µ ÑÐ stating that in any (first-order) model for ÑÐ ½ formula fv ÑÐ µ ÑÐ is satisfied. 3. General Algebraic Data Types We introduce an extension of the Hindley/Milner system with a general form of algebraic data types. The constraint domain is user-customizable by providing an appropriate set of Constraint Handling Rules (CHRs) [3]. The language of expressions, types, constraints and CHRs is as follows. Expressions Ã Ü Ü Ð Ø Ò Ð Ø µ Ø Ó Ò Ô Á Patterns Ô Ü Ô Ôµ Ã Ô Types Ø Ø Ø Ì Ø Constraints Ø Ø Í Ø Type Schemes Ø «µ Ø CHRs Ê Í Ø µ Í ½ Ø ½ Í Ò Ø Ò µ We define a standard functional language extended with case expressions to support pattern matching over user-definable date types. Note that in examples we will use pattern matching notation for convenience. We assume that à refers to constructors of user-defined data types. As usual patterns are assumed to be linear, i.e., each variable occurs at most once. For simplicity, we only consider variable patterns, pair patterns and unary constructor patterns. We also support type annotations in our language. Our annotations are closed, i.e. all variables appearing in µ Ø are assumed to be universally quantified /4/13
6 (Eq) Ø È Ô Ø Ø ¼ Ø ¼ (Abs) Ü Ø ½ Ø Ü Ø ½ Ø (App) ½ Ø Ø Ø (Var) Ú ¼ µ ص È Ô Ø ¼ ½ Ø Ú Ø Ø (Case) Ø ½ Ô Ø ½ Ø for Á Ó Ô Á Ø (Pat) Ô Ø ½ Ôµ fv Ø µ Ô Ø Ô Ø ½ Ø (Let) ½ ½ Ø ½ fv ½ Ø ½ µ fv µ (LetA) fv ½ Ø ½ µ ½ ½ µ Ø ½ µ ½ Ø ½ ½ µ Ø ½ µ Ø ½ µ Ø ½ µ Ø Ð Ø ½ Ò Ø Ð Ø ½ µ Ø ½ Ò Ø ½ (Pat-Var) Ü Ø Ì ÖÙ Ü Ø µ (Pat-Pair) Ô ½ Ø ½ ½ ½ Ô ½ µ Ô Ø Ô µ Ô ½ Ô µ Ø ½ Ø µ ½ ½ Ô ½ Ô ½ µ (Pat-K) à µ Ø Ì Ô Ø Ø ¼ ¼ Ôµ Ã Ô Ì Ø ¼ ¼ Ø Ôµ Figure 1. Typing Rules Our type language is standard. We assume that Ì Ø refer to user-definable data types. Although implicit, we may make use of pairs and lists in examples. A primitive constraint is either an equation Ø Ø ¼ (a.k.a. type equality) or an Ò-ary user-defined constraint Í Ø. In case we consider type classes, we may refer to Í Ø as a type class constraint. We assume a special (always satisfiable) constraint Ì ÖÙ representing the empty conjunction of constraints, and a special (never satisfiable) constraint Ð. Often, we treat conjunctions of constraints as sets and abbreviate Boolean conjunction by,. We generally use symbols and to refer to sets of constraints. Type schemes have an additional constraint component which allows us to restrict the set of type instances. We often refer to a type scheme as a type for short. Note that we consider Ø as a short-hand for Ì ÖÙ µ Ø. The presence of equations makes our system slightly more general compared to standard Hindley/Milner. E.g., types µ and are equivalent. Equations will become interesting once we allow them to appear in type assumptions of constructors. We assume that data type definitions are pre-processed. E.g., in example programs we write Ø Ì ½ ººº Ñ ÓÖ ÐÐ ½ ººº Òº Ã Ø which implies that à µ Ø Ì Ò Ø where Ò Ø is some initial environment. We assume that and fv ص. We commonly refer to as the set of universally bound variables and to as the /4/13
7 set of existentially bound variables. As it is common, we usually group together constructors belonging to the same type. However, we disallow multiple definitions such as à ½ ÓÓ and à ½ Ö. The meaning of constraints is described in terms of some set È Ô of CHRs. We commonly refer to È Ô as the program theory. CHRs are a high-level notation to write incremental constraint solvers, defining a rewrite relation from one constraint store (i.e. set of constraints) to another. For our purposes, we restrict ourselves to single-headed simplification CHRs Í Ø µ and multi-headed propagation CHRs Í ½ Ø ½ Í Ò Ø Ò µ. For the moment, we are only interested in the logical reading of CHRs. E.g. Í Ø µ can be interpreted as Í Ø µ where fv ص and fv µ, and Í ½ Ø ½ Í Ò Ø Ò µ can be interpreted as Í ½ Ø ½ Í Ò Ø Ò µ µ where fv Ø ½ Ø Ò µ and fv µ. We assume that if È Ô appears in a logical statement then È Ô refers to the conjunction of logical readings of CHRs in È Ô. The subset of CHRs we consider is already Turing complete and allows for a natural representation of type class relations [27, 4]. E.g., the CHRs (A1-5) in Example 4 result from the following type class program. Ø ÖÓ ÖÓ Ø ËÙ Ü ËÙ Ü Ð Ð Ñ Ò Ð Ñ ¹ Ò ¹¹ µ Ò Ø Ò ÖÓ Ñ Ñ ¹¹ ½µ Ò Ø Ò Ð Ñ Ò Ë٠е Ñ ËÙ Òµ ¹¹ µ Instances (A1-2) correspond directly to CHRs (A1-2). The functional dependency Ð Ñ ¹ Ò enforces that the sum parameter Ò is uniquely determined by Ð and Ñ and is represented by the CHR (A3). CHRs (A4-5) enforce the functional dependency on each instance. We have now everything in place to describe the set of well-typed programs. The typing rules can be found in Figure 1. We make use of judgments Ø where is a constraint, is an environment, an expression and Ø a type. None of the typing rules affects the program theory È Ô, hence, we leave È Ô implicit. A judgment Ø is valid iff we can derive it via the rules in Figure 1. We give an overview of the most interesting rules. In rule (Var) we assume that Ú either refers to a variable Ü or constructor Ã. We can build a type instance of a type scheme if we can verify that the instantiated constraint is logically contained by the given constraint under the given program theory. This is formally expressed by the side condition È Ô Ø ¼. Rules (Case) and (Pat) deal with pattern matching. Rule (Pat) is in particular interesting. Silently, we consider Ô as a (special purpose) expression only appearing in intermediate steps. We make use of an auxiliary judgment Ô Ø Ôµ to establish a relation among pattern Ô of type Ø and the binding Ô of variables in Ô. Constraint arises from constructor uses in Ô. Variables refer to all existential variables. Notation will become more clear in the type inference section. Note that side condition fv Ø µ prevents existential variables from escaping. Also note that we type the body of the pattern clause under the temporary type assumption and environment Ô arising out of Ô. The rules for the auxiliary judgment are as follow. In rule (Pat-Pair) we assume that there are no name clashes between variables ½ and. In rule (Pat-K) we assume that variables and are fresh. Rule (Pat-Var) is standard. In rule (Eq) we can change the type of expressions. Note that the set of constraints may not necessarily be the same in all parts of the program (see rule (Pat)). Therefore, this rule plays a crucial role when typing pattern clauses. In rule (Let) we couple the quantifier introduction rule with the introduction of user-defined functions. In our formulation, does not necessarily guarantee that ½ is satisfiable. However, our rule (Let) is sound for a lazy semantics which applies to Haskell. See [22, 31] for a discussion /4/13
8 ½ W ½ Ø ½ µ (Var) Ú µ ص Ú W ص (App) W Ø µ Ø fresh ½ Ø ½ Ø Ø (Abs) fresh Ü W ص Ü W ص ½ W ص (Case) Ô W Ø ¼ µ for Á W Ø µ Î Ø ½ Ø fresh Ø ½ Ø Ø Á Ø ½ Ø ¼ µ (Pat) Ô Ô Ø ½ µ Ô W Ø µ Ø fresh fv Ø µ µ Ø Ø ½ Ø Ó Ô Á W Ø µ Ô W ص fv ½ Ø ½ µ ½ W ½ Ø ½ µ ½ µ Ø ½ µ ½ W ½ Ø ¼ ½ µ (Let) ½ ÓÐÚ ½ È Ô µ fv ½ Ø ½ µ fv µ ½ µ Ø ½ µ W Ø µ (LetA) ½ µ Ø ½ µ W Ø µ ½ Ø ½ Ø ¼ ½ µ fv Ø ¼ ½ µ ½µ Ð Ø ½ Ò W Ø µ Ð Ø ½ µ Ø ½ ½ Ò W Ø µ (Pat-Var) Ø fresh Ü Ì ÖÙ Ü Ø Øµ (Pat-Pair) Ô ½ ½ ½ Ô ½ Ø ½ µ Ô Ô Ø µ Ô ½ Ô µ ½ ½ Ô ½ Ô ½ Ø ½ Ø µµ (Pat-K) à µ Ø Ì Ô ¼ ¼ Ô Ø Ô µ m.g.u. of Ø Ô Ø Ã Ô ¼ ¼ µ Ôµ Ì µµ Figure 2. Type Inference Rule (LetA) introduces a closed type annotation. Silently, we assume that variables appearing in ½ µ Ø ½ are fresh to avoid name clashes. We allow for polymorphic recursive functions, however, we leave out the rule for monomorphic recursive functions for brevity. For simplicity, we omit giving a meaning to programs. In case we are modelling type classes we can easily adopt the dictionary-translation scheme described in [6]. Note that we silently assume that deep patterns are translated to shallow patterns by imposing a specific evaluation order, e.g. left-to-right. As pointed out in Section 1.1 our system subsumes the previous systems of existential types [18], singleparameter type classes with existential types [17] and GRDTs [35]. Furthermore, we can extend Läufer s system [17] to type class extensions such as multi-parameter classes and functional dependencies. 4. Type Inference We introduce a deduction system in style of algorithm Ï where we generate constraints out of the program text and solve them before building type schemes at let statements. The significant difference to standard Hindley/Milner is that we need the following richer domain of implication constraints to express the typing /4/13
9 problem. Constraints Ø Ø Í Ø ImpConstraints µ In our type system we only admit (sets of primitive) constraints. Hence, we need to give a characterization of solutions of implication constraints to achieve type inference. DEFINITION 1 (Solved Forms). Let È Ô be a program theory, an implication constraint and a constraint. We say is a solved form of w.r.t. È Ô iff È Ô. In such a situation, we write ÓÐÚ È Ô µ. We say is a principal solved form iff (1) is a solved form, and (2) for any other solved form ¼ we have that È Ô ¼. fv µ The above definition is a generalization of a similar notion found in [22, 31]. Note that in case implication constraints are conjunction of equations we find that solved forms correspond to unifiers. Note that our notion of solvability of implication constraints also subsumes unification under a mixed prefix [20]. E.g., assume all constraints to the left of are Ì ÖÙ. Based on our notion of solved forms we can define a algorithm Ï style inference system in Figure 2. We make use of judgments of the form W ص where environment, and expression are input values and implication constraint and type Ø are output values. For patterns we introduce an auxiliary judgment of the form Ô Øµ to compute the set of existential variables, constraint, environment and type Ø arising out of pattern Ô. Note that the statement Ø fresh is meant to introduce a fresh type variable Ø. We briefly review the individual rules. Note that we write to denote syntactic equality. In rules (Var-x) and (Pat-K) we assume that the bound variables and are fresh. In rule (Pat) we make use of the implication constraint fv Ø µ µ which states that under the temporary assumptions arising out of the pattern Ô we can satisfy the implication constraint arising out of. The quantifier ensures that no existential variables escape. Note that fv Ø µ is a short-hand for where fv µ fv Ø µ. That is, we existentially quantify over all variables which are strictly local in. Note that in case of (existential) algebraic data types the constraint equals Ì ÖÙ and is a constraint. In rule (LetA) we again make use of implication constraints to represent the subsumption problem among two type schemes. In rule (Let) we need to solve implication constraints before we can build the type scheme. Solved forms ensure that we can construct a typing derivation, i.e. a proof tree making use of the rules in Figure 1. THEOREM 1 (Soundness of W ). Let È Ô be a program theory, an environment, an expression, an implication constraints and Ø a type such that W ص. Let be a solved form of fv. Then ص Ø. Assuming that ÓÐÚ is decidable we obtain sound and decidable type inference. To illustrate the inference process we consider a (contrived) example making use of multi-parameter type classes with existential types. EXAMPLE 5. Consider Ð ÓÓ Û Ö ÓÓ ¹ ¹ ÁÒØ Ò Ø Ò ÓÓ ÁÒØ ¹¹ µ Ð Ö Û Ö Ö ¹ ¹ Ø Ö ÓÖ ÐÐ º Ö Ã½ µ ÓÖ ÐÐ º à µ ý µµ Ö Ã µµ ÓÓ where instance (F) is modelled by È Ô (F) ÓÓ ÁÒØ µ Ì ÖÙ and the method and constructor declarations are recorded in some initial environment. E.g., ÓÓ ÓÓ µ ÁÒØ and /4/13
10 Ö Ö µ are in Ò Ø. Here is the (slightly simplified) implication constraint arising out of s program text. Note that Ø refers to the type of. Ø Ö Ø Ø Ø ½ Ø Ø Ö Ö Ø ½ µ Ì ÖÙ ÓÓ Ø ÁÒص We find that Ø Ö Ø Ø Ø ½ Ø Ø ½ Ø ÁÒØ Ø ½ is a solved form. Constraint Ø ½ is important to solve implication (1). Note that under È Ô we find that Ø Ø ½ Ø ÁÒØ Ø ½ solves (2) (we can conclude that ÁÒØ and ÓÓ ÁÒØ holds for any ). Hence, after normalizing types by applying the m.g.u. we find that has type Ö ÁÒØ ÁÒØ. We also achieve completeness under the assumption that principal solutions exist. Assume that for each implication constraint we either find a principal solved form or no solved form exists at all. Let s call this the principal implication constraint property. THEOREM 2 (Completeness). Assume È Ô satisfies the principal implication constraint property. Let Ø such that Then, W Ø ¼ µ such that È Ô Ø ¼ Ø ¼ ص where ¼ is a principal solved form of. In particular, we find that principal solved forms imply principal types. Let È Ô be a type class theory, an environment and an expression. We say ص is a principal type iff (1) Ø, and (2) if ¼ Ø ¼ then È Ô ¼ Ø Ø ¼ µ. As an immediate consequence the following holds. COROLLARY 1. The principal implication constraint property implies principal types. However, the principal implication constraint property does not hold in general. Solved forms are from a less expressive constraint domain. Hence, we cannot maintain equivalence among implication constraints and their solved forms in general. Here is a (contrived) example making use of multi-parameter type classes and existential types. EXAMPLE 6. Consider Ø Ö ÓÖ ÐÐ º Å Ü Å Ýµ ÓÓ Ü Ý where we assume a binary constraint symbol ÓÓ on which we impose the CHRs È Ô (F1) ÓÓ ÁÒØ µ Ì ÖÙ (F2) ÓÓ ÓÓÐ µ Ì ÖÙ modeling some type class instance declarations. In some initial environment we find Ò Ø ÓÓ ÓÓ µ ÁÒØ Å Ö modelling the data type definition and a type class declaration. The implication constraint describing the type of is as follow: ½µ µ Ø Ö Ì ÖÙ ÓÓ ÁÒصµ Function can be given types Ø ÁÒØ Ö ÁÒØ and Ø ÓÓÐ Ö ÁÒØ. E.g., Ø ÁÒØ Ö ÁÒØ solves the above implication constraints in combination with the CHR (F1) but also Ø ÓÓÐ Ö ÁÒØ is a solution (using CHR (F2)). Note that both types are incomparable and there is no more general type. In the next section, we introduce concrete procedures for solving of implication constraints. 5. Solving of Implication Constraints We first review the operational semantics of CHRs which can be described in terms of rewritings of constraint stores (Section 5.1). Then, we introduce a generic solver for implication constraints which is parameterized in terms of the CHR solver for the program theory (Section 5.2). Our solver is incomplete in general. This is not surprising given the expressiveness of our system. For the important case of multi-parameter type classes with existential types we identify some sufficient conditions under which solving is complete (Section 5.3) /4/13
11 5.1 CHR Solving The operational reading of CHRs is simple. In case of propagation rules we add the rhs if we find a matching copy of the lhs in the constraint store. In case of simplifications rules we remove the matching copy and replace it by the rhs. The formal definition is as follows. DEFINITION 2 (CHR Solving). Let È Ô be a set of CHRs. Let ʵ ½ Ò µ ½ Ñ È Ô and be a constraint. Let be the m.g.u. of all equations in. Let ¼ ¼ ½ Ò such that there exists a substitution on variables in rule (R) such that µ ¼ µ for ½ Ò. Then, Ê ½ Ñ. Let ʵ µ ½ Ñ È Ô and be a constraint. Let be the m.g.u. of all equations in. Let ¼ such that there exists a substitution on variables in rule (R) such that µ ¼ µ, that is user-defined constraint ¼ matches the left-hand side of rule (R). Then, Ê ¼ ½ Ñ. Often, we perform some equivalence transformations (e.g. normalize equations by building the m.g.u. etc) which are either implicit or explicitly denoted by. A derivation, denoted È ¼ is a sequence of derivation steps using rules in È such that no further derivation step is applicable to ¼. CHRs are applied exhaustively, being careful not to apply propagation rules twice on the same constraints (to avoid infinite propagation). We say a set of CHRs is terminating if for each there exists ¼ such that È ¼. Note that CHRs are sound in the sense that if È ¼ then È ¼ fv µ. We refer to this as the CHR Soundness Result. EXAMPLE 7. Recall the CHRs defined in Example 4. We have that (A1) ÖÓ Ñ Ñ µ Ì ÖÙ (A2) Ë٠е Ñ ËÙ Òµ µ Ð Ñ Ò (A3) Ð Ñ Ò ½ Ð Ñ Ò µ Ò ½ Ò (A4) ÖÓ Ñ Ò µ Ñ Ò (A5) Ë٠е Ñ Ò ¼ µ Ò ¼ ËÙ Ò ËÙ ÖÓµ Ñ Ò ËÙ ÖÓµ Ñ Ò ¼ Ñ ÖÓ ËÙ ÖÓµ Ñ Ò Ñ ÖÓ Ò Ò ¼ ËÙ ÖÓµ ÖÓ Ò Ñ ÖÓ Ò Ò ¼ ËÙ ÖÓµ ÖÓ ËÙ Ò ¼¼ µ Ò ËÙ Ò ¼¼ Ñ ÖÓ Ò Ò ¼ ½ ÖÓ ÖÓ Ò ¼¼ Ò ËÙ Ò ¼¼ Ñ ÖÓ Ò Ò ¼ ÖÓ ÖÓ ÖÓ Ò ËÙ ÖÓ Ò ¼¼ ÖÓ Ñ ÖÓ Ò Ò ¼ Ò ËÙ ÖÓ Ò ¼¼ ÖÓ Ñ ÖÓ Ò Ò ¼ Note that we assume set semantics (see the first CHR derivation step). In the third and fifth step, we perform some implicit equivalence transformation steps. 5.2 Generic Implication Solver We are given a program theory È Ô and an implication constraint. Our task is define a solving procedure such that either ÓÐÚ È Ô µ Ë and Ë is a solved form for w.r.t. È Ô, or the solving procedure fails. Note that solving is easy for the primitive case. Assume, implication constraint is equivalent to where is a constraint. Immediately, we can define ÓÐÚ È Ô µ ¼ where ¼ and È ÈÔ Ô is the program theory. In essence, this is the kind of solving considered in HM(X) [22, 31] assuming that the constraint domain X is specified by È Ô /4/13
12 The more general case is to solve constraints of the form ¼ µ. For simplicity, we omit quantifiers and assume that ¼, and are sets of primitive constraints. Our strategy is to execute ¼ È Ô ¼ and ¼ ¼ based on the CHR solver defined by È ÈÔ Ô. Then, we observe final stores ¼ and ¼. If both are logically equivalent we can conclude that the initial store must be logically equivalent (follows from Soundness of CHR Solving). Hence, we can conclude that ¼ µ is solved by ¼. Note that ¼ µ is equivalent to ¼ ¼. Otherwise (final stores disagree), we attempt to add some constraint such that solving will eventually be successful. E.g,, for the above case we can argue that adding the set difference between ¼ and ¼ will lead to success. Thus, we continue solving with ¼ ¼ ¼ µ. One of the problems is that the constraint ¼ ¼ may invalidate the result so far. E.g., ¼ ¼ ¼ becomes Ð. Another problem is that we will need to respect nested quantifiers. For example, consider solving of Ö ÓÓ µ. By ignoring the quantifier the obvious solution seems to be ÓÓ which is invalid because the universally quantified variable escapes. Less of a problem is the case of nested implications such as ½ ½ ½ µ. We simply solve implication constraints inductively. Based on the above observations we define our generic implication solver which is parameterized in terms of the underlying CHR solver as follow. DEFINITION 3 (Implication Constraint Solver). Let È Ô be a program theory and an implication constraint. Primitive: We define ÓÐÚ È Ô µ ¼ where È Ô ¼ if. General: Otherwise ¼ ½ µ where ¼ and are conjunction of primitive constraints and ½ and are implication constraints and fv µ fv ¼ µ. 1 We inductively compute (1) ÓÐÚ ¼ È Ô µ ¼ and (2) ÓÐÚ ¼ ½ È Ô µ ¼ for some ¼ and ¼. We distinguish among the following cases. Solved: We define ÓÐÚ È Ô µ ÓÐÚ ¼ È Ô µ if Î ¼ µ Î ¼ µ where Î fv ¼ µ. Add: We define ÓÐÚ È Ô µ ÓÐÚ Ë È Ô µ if Î ¼ µ Î ¼ µ where Î fv ¼ µ and Ð ¼ and Ë is a conjunction of primitive constraints such that (3) È Ô ¼ Ë, (4) fv ˵ fv ¼ µ and (5) È Ô ¼ Ë. Failure: We define ÓÐÚ È Ô µ Ð in all other cases. The definition of our solver is kept very general. Conditions (3-5) give only a characterization which subset of primitive constraints in the final store of derivation (2) may prove useful to solve the implication constraint ½ µ. The least we require is the following. Condition (3) ensures that we only add in useful constraints. Condition (4) serves two purposes. First, we must prevent existentially bound variables from escaping. Second, we avoid the introduction of new variables. This is crucial to verify that the above characterization of implication solving terminates. Condition (5) has a similar purpose. We avoid adding in redundant constraints. We can state the following results for any concrete solver instance satisfying Definition 3. LEMMA 1 (Termination). Let È Ô be a terminating program theory and an implication constraint. Then ÓÐÚ È Ô µ for some constraint or we report failure. We can also guarantee that our solving method is sound. LEMMA 2 (Soundness). Let È Ô be a program theory, be an implication constraint and a constraint such that ÓÐÚ È Ô µ. Then, is a solved form of w.r.t. È Ô. 1 The last condition is satisfied by construction for all implication constraints generated /4/13
13 Depending on the particular application domain we may want to improve our solver. E.g., applying more sophisiticated methods to identify a suitable subset Ë, switching the order of implication constraints to obtain better results etc. Clearly, there must be a trade-off between precision and efficiency as we will see shortly. In our actual solver implementation in Chameleon [32] we demand that each node in an implication constraint invokes at most one add step which then must be followed by either a solved or fail step. Furthermore, we combine the result of add steps from conjunctions of implication constraints rather than processing implications in a fixed order. Let s consider the complexity of such a solving strategy. Assume we solve consisting of Ò individual constraints of the form ¼ where the maximal depth of any of the ¼ is Ñ. By depth we refer to the number of nested implications. For convenience, we assume that each ¼ has again Ò conjunctions of sub-implications until ¼ is a set of primitives (we could artificially enforce this assumption). Then, we can conclude that under our solver strategy there will be Ç Ò Ñ µ CHR solver invocations (we may pass through Ñ nodes and at each node we invoke the CHR solver Ò times). We believe that Ñ will not be very high for realistic programs. Thus, we achieve tractable inference. The question is whether our implemented solver is good enough. It is time to consider some examples of implication solving. We revisit Example 5. EXAMPLE 8. We have that È Ô (F) ÓÓ ÁÒØ µ Ì ÖÙ. We consider solving of the following implication constraint. For brevity, we use, instead of. Ø Ö Ø Ø Ø ½ Ø Ø ¼ µ Ö Ö Ø ½ µ ½ ½ µ Ì ÖÙ ÓÓ Ø ÁÒص µ In the following calculations we leave the program theory È Ô implicit. We apply the solver strategy as implemented. That is, we solve conjunctions of implications concurrently. Step 1: In case of ¼ ½ ½ µ we compute ÓÐÚ Ø Ö Ø Ø Ø ½ Ø Ø Ö µ Ø Ö Ø Ø Ø ½ Ø Ø Ö ¼ ½ µ ÓÐÚ Ø Ö Ø Ø Ø ½ Ø Ø Ö Ø ½ µ Ø Ö Ø Ø Ø ½ Ø Ø Ö Ø ½ ¼ ½ µ Constraints ¼ ½ and ¼ ½ are not logically equivalent w.r.t. Î Ø Ø ½ Ø Ø. However, we find Ë ½ Ø ½ (which satisfies conditions (3-5)). In case of ¼ µ a similar calculations yields Ë Ø ÁÒØ. Note that ÓÓ cannot be added, otherwise variable escapes. We add the combined results. Step 2: We consider now Ø Ö Ø Ø Ø ½ Ø Ø ¼ µ Ø ½ Ø ÁÒØ Ë ½ Ë µ Ö Ø ½ µ ½ ½ µ Ì ÖÙ ÓÓ Ø ÁÒص µ For the first implication we can immediately report solved. Note that for the second implication, we compute ÓÐÚ Ø Ö Ø Ø Ø ½ Ø Ø Ø ½ Ø ÁÒØ µ Ø Ö Ø Ø Ø ½ Ø Ø Ø ½ Ø ÁÒØ ¼ µ and ÓÐÚ Ø Ö Ø Ø Ø ½ Ø Ø Ø ½ Ø ÁÒØ ÓÓ µ Ø Ö Ø Ø Ø ½ Ø Ø Ø ½ Ø ÁÒØ ¼ µ /4/13
14 because Ø Ö Ø Ø Ø ½ Ø Ø Ø ½ Ø ÁÒØ ÓÓ Ø Ö Ø Ø Ø ½ Ø Ø Ø ½ Ø ÁÒØ We find that ¼ and ¼ are equivalent w.r.t. Î Ø Ø ½ Ø Ø. Hence, the second implication is solved too. We report Ø Ö Ø Ø Ø ½ Ø Ø Ø ½ Ø ÁÒØ as the final result. Note that if we solve implications in a strict order we may fail. By strict solving order we assume that for each implication we must add until we reach solved only then we consider the next implication. Assume we employ this solving strategy for the above example. Assume we start solving ¼ µ. As shown above, we add Ø ÁÒØ. Under a strict solving order, we continue solving with ¼ Ø ÁÒØ µ which can only be solved if we add Ø ½. However, it is not obvious how to discover Ø ½ unless we consider solving of ¼ ½ ½ µ first. Hence, we fail under a strict order solving strategy. The next example shows that in general there is no other choice than to solve implications in all possible orders. Thus, solving may become more expensive. EXAMPLE 9. Consider the following program making use of existential types and multi-parameter type classes with functional dependencies. Ð ½ Û Ö ½¹ ¹ ¹ ÁÒØ Ò Ø Ò ÁÒØ ÁÒØ Ð ¹ Û Ö ¹ ¹ ¹ ÁÒØ Ò Ø Ò ÁÒØ ÁÒØ Ø Ö ½ ÓÖ ÐÐ º ý ½ µ ÓÖ ÐÐ º à ½ µ ¹¹ Ö ÁÒØ ÁÒØ ¹ ÁÒØ ÁÒص ý ½ µµ ½ ½ ÁÒصµ à ½ µµ ½ ÙÒ Ò µ Note that Hugs and GHC both fail to infer a type for and only succeed if we include s type annotation. We can therefore expect that solving is hard here. The translation from type classes to CHRs yields È Ô (F) ÁÒØ ÁÒØ µ Ì ÖÙ (G1) ÁÒØ ÁÒØ µ Ì ÖÙ (G2) ÁÒØ µ ÁÒØ (G3) ¼ µ ¼. The (simplified) implication constraint is as follow. Ø Ö ½ ÁÒØ ÁÒص Ì ÖÙ ½ ½ ÁÒص ½µ Ì ÖÙ ½ µ µ Note that there is a mutually dependency between both branches. Let s attempt to solve the implications. We first consider (1), we can only add ½ ÁÒØ. Next, we consider (2). note that ½ ÁÒØ and ½ imply, via CHR (G2), that ÁÒØ which can be added. So far, we added ½ ÁÒØ ÁÒØ. We consider again (1), this time ½ can be resolved to Ì ÖÙ under ½ ÁÒØ ÁÒØ via CHR (F). A similar observations shows that ½ resolves to Ì ÖÙ. Hence, Ø Ö ½ ÁÒØ ÁÒص ½ ÁÒØ ÁÒØ is a solution. Note that our implemented solver fails too. We attempt to solve implications concurrently but we would need several iterations to discover that all implications can be solved. We summarize the results of this section. Our generic solver supports type inference for all instances of our framework. The definition of our solver is left flexible to allow for future improvements. We have implemented a particular instance of our solver which is tractable but may fail for some examples. However, our solver is open for improvement, on the expense that solving becomes more costly. We believe that our implemented /4/13
15 solver strictly improves over the methods implemented in GHC [5] which also supports advanced extensions of algebraic data types. Unfortunately, we are unable to conduct a formal comparison due to a lack of a formal description of GHC s type inference engine. We refer to Appendix C where we consider a few more examples. There is certainly a clear limit how much we can improve our solver. E.g., finding a solution may be too costly or even impossible. We do not want to reject such cases before-hand. Hence, we may fail unexpectedly. However, our solver has the pleasant property of supporting the type error reporting methods developed in [30, 29]. Hence, we can supply the user with some detailed information which constraints are responsible for failure, are any existential variables involved, from which program location do these constraints arise from etc. We believe that this is a much more valuable property than guaranteeing completeness. In the upcoming section, we show how to achieve complete solving for multi-parameter type classes with existential types. That is, we identify some conditions under which we find principal solutions or no solutions exist. 5.3 Multi-Parameter Type Classes with Existential Types We define MPTC program theories as those that satisfy the following three restrictions. 1. CHRs are single-headed simplification rules where we only find user-defined constraints or Ì ÖÙ on righthand sides. 2. The rules are range-restricted. We say a CHR is range-restricted iff grounding all variables on the left-hand side of a CHR, grounds all variables on the right-hand side. 3. The CHRs are terminating and confluent. We say a set of CHRs is confluent iff any order of rule applications yields to the same final store. The first condition ensures that CHR derivations cannot lead to failure. The last two conditions ensure that the CHR solver is complete, which is clearly necessary for the implication solver to be complete. Note that the conditions imposed on Haskell type classes [7] guarantee termination and confluence. We can easily check for range-restriction by verifying that the set of variables on the right-hand side of a variable is already mentioned on the left-hand side. The MPTC program theories are sufficient to model a significant subset of multi-parameter type classes [14, 27] with existential types. For simplicity, we neglect super-classes. In our first result, we show that under these assumptions we can locally compute principal solved forms. In preparation, we normalize implication constraints based on the following first-order equivalences: (i) ½ É µ É ½ µ where fv ½ µ and (ii) É ½ µ É µ É ½ µ where fv µ, fv ½ µ and É and (iii) ½ µ ½ µ. We exhaustively apply the above identities from left to right. Hence, w.l.o.g. we assume that implication constraints are of the form É ¼ ½ ½ µ Ò Ò µ (1) where É is a mixed prefix of the form ¼ ½ ½ Ò Ò. We apply skolemization [20] to remove universal quantifiers. That is, we transform into Ë µ where Ë s are some fresh Skolem constructors. We apply this step repeatedly until we reach the form ¼ ¼ ¼ ½ ¼ ½ µ ¼ Ò ¼ Ò µ (2). Note that we leave the remaining existential quantifier implicit in (2). In general, Skolemization is only a satisfiability-preserving but not an equivalence-preserving transformation. However, in our specific case we can state that (1) is equivalent to (2). The crucial point here is that ¼ (respectively ) consist of conjunctions of user-defined constraints only and none of the CHRs reduces to Ð. Hence, any solved form of (2) is also a solved form of (1). Next, we introduce a procedure to compute principal solved forms locally. LEMMA 3 (Local Principal Solved Forms). Let È Ô be a MPTC theory and ¼ µ be a normalized MPTC implication constraint such that ¼ ¼ and ¼ ¼ for some ¼ and ¼. Let Ë be the set difference between ¼ and ¼, i.e. Ë ¼ ¼. Then, ¼ Ë is a principal solved from of if (1) Ë does not contain Ð and (2) each user-defined constraint in Ë does not refer to a Skolem constructor and (3) has a solved form /4/13
16 Condition (1) is obvious. Condition (2) prevents existential variables (which are Skolemized in the normalized constraint) from escaping. Condition (3) is interesting. If has a solved form, then adding the difference among final stores yields a principal solved form. A proof can be found in Appendix B.1. Our next result (which holds for arbitrary program theories and implication constraints) allows us to combine the locally computed principal solved forms. LEMMA 4 (Combining Principal Solved Forms). Let È Ô be a program theory. Let ½ and be two implication constraints and Ë ½ and Ë be two constraints such that Ë ½ is a principal solved form of ½ and Ë is a principal solved form of. Then, Ë ½ Ë is a principal solved form of ½. Immediately, we can state the following result. THEOREM 3 (Principal Types for MPTC). We can infer principal types for multi-parameter type classes satisfying the MPTC conditions if local principal solutions exist. The test for local principal solutions involves verifying conditions (1-3) in Lemma 3. Note that conditions (1) and (2) can be easily checked. To verify condition (3) we can run our generic solver to check whether ¼ Ë is a solved form (note that the lemma guarantees then that ¼ Ë must be principal). A subtle point is that local principal solutions are not a necessary condition to obtain principal types. EXAMPLE 10. We assume È Ô (F1) ÓÓ ÁÒØ µ Ì ÖÙ (F2) ÓÓ ÓÓÐ µ Ì ÖÙ. Consider Ì ÖÙ ÓÓ µ Ì ÖÙ ÁÒص which yields Ì ÖÙ ÓÓ Ë µ Ì ÖÙ ÁÒص after normalization. Note that Ì ÖÙ ÓÓ Ë µ has no local principal solved form. E.g., ÁÒØ and ÓÓÐ are two incomparable solutions. Note that our local principal solved form procedure (Lemma 3) does not apply. Condition (2) is not satisfied because Ë ÓÓ Ë. However, we find that ÁÒØ is a principal solution. To obtain principal types for MPTC in general we need to impose one further restriction. The above example suggests that we are in trouble if constraints are impure. That is, we find a constraint ÓÓ Ë which contains a mix of existentially quantified and Skolemized variables. We say a constraint is pure iff either all parameters in a user-defined constraint refer to existentially quantified variables, or refer to Skolemized variables. For pure MPTC systems we can guarantee that local principal solved forms are a necessary condition to achieve principal types. 6. Related Work The HMG(X) system by Simonet and Pottier [26] is very close to our system in terms of typing rules. A significant difference is that our constraint domain is user-programmable in terms of CHRs whereas their constraint domain is left abstract. We acknowledge that the abstraction from program text to implication constraint (first step in our inference system) is adopted from [26]. Although, we believe that the essence of this idea is already present in Zenger s work [36]. Their main concern is to achieve complete and tractable inference which they achieve for the special-purpose case of GRDT under some sufficient conditions. In contrast, we provide for a more general and wider applicable solver. The goal of the work by Peyton-Jones, Washburn and Weirich [15] is to make type inference for GRDT complete and predictable. The gist of their work is to impose the condition that if the type of the body of a pattern clauses changes due to a GRDT, then the GRDT must be explicitly annotated by the programmer. At this stage, we would like to reiterate the point that inference can never be predictable due to unavoidable type errors. Therefore, we do not impose any such conditions. Thus, our solver specialized to GRDT is more likely to succeed. Note that the GRDT extension by Peyton-Jones, Washburn and Weirich [15] is incorporated into the latest GHC [5] version. However, their system seems to behave differently in case of type class extensions with existential types. We refer to Appendix C for details. Hughes [9] considers restricted data types which superficially resemble our form of algebraic data types in the specific case of type classes. The crucial difference is that our system follows the object-oriented view, /4/13
17 i.e. type class constraints attached to constructors are turned into additional dictionary parameters. The approach by Hughes seems more flexible, but the actual design is also more subtle. 7. Conclusion We have presented an extension of Hindley/Milner with a CHR programmable constraint domain to support a general form of algebraic data types (see Section 3). Our system unifies common forms [18, 17, 35] and provides the basis for some implemented but not well-studied forms such as multi-parameter type classes with existential types. We can also support some novel variants such as Example 4. Based on a characterization of solutions of implication constraints we could provide for an algorithm Ï style inference system (see Section 4). Type inference is shown to be tractable by advancing the state of art of constraint solving (see Section 5). The Chameleon system [32] implements the ideas in this paper and extends the expressiveness of languages such as Haskell significantly. For presentation purposes, we decided on a algorithm Ï style inference system. Such algorithms are wellunderstood and can be found in many implementations. However, in our own recent work we found that algorithm Ï has some inherent limitations. The details are subtle but may become important when considering advanced type extensions such as those considered here. We refer to [33] for details. There is lots of scope for future work. E.g., we plan to explore further the expressiveness of our system along the following lines. What kind of program properties can be encoded in terms of CHRs and checked by our system, what kind of programming patterns can be represented etc. In Appendix D we briefly sketch how our system can support an extension of GRDT with type level functions. Another topic is to identify further instances of our system for which solving is complete, i.e. yields principal solutions. The problem we are facing is known as constraint abduction in the constraint world. Based on some recent work [19], we hope to improve our inference results for specific instances such as GRDT [28]. In another direction we would like to explore more expressive but still tractable constraint domains. Hinze and Peyton-Jones [8] explore the possibility of adding higher-order instances to Haskell. Here is a simple example. Ð Û Ö Ð Û Ö Ò Ø Ò ÓÖ ÐÐ º ¹ µµ ÁÒØ ÓÓе Û Ö µ ½ ÌÖÙ µ Notice the use of µ which is not admitted in the constraint domain of the system in Section 3. We envision an extension where such higher-order instances are encoded in terms of higher-order CHRs. Instance (G) could then be represented via ÁÒØ ÓÓе µ µ µ Ì ÖÙ µ. That is, during constraint solving we may make use of temporary CHRs. We believe that the combination of higher-order CHRs and implication constraints for constraint solving will be able to support type inference for exciting extensions such as higher-order instances and higher-rank types. Acknowledgements We thank Jeremy Wazny for useful discussions and helping us with the implementation. References [1] J. Cheney and R. Hinze. First-class phantom types. Technical Report CUCIS TR , Cornell University, [2] L. Damas and R. Milner. Principal type-schemes for functional programs. In Proc. of POPL 82, pages ACM Press, January [3] T. Frühwirth. Constraint handling rules. In Constraint Programming: Basics and Trends, LNCS. Springer-Verlag, [4] P. J. Stuckey G. J. Duck, S. Peyton-Jones and M. Sulzmann. Sound and decidable type inference for functional dependencies. In Proc. of ESOP 04, volume 2986 of LNCS, pages Springer-Verlag, /4/13
Extensional Equality in Intensional Type Theory
 Extensional Equality in Intensional Type Theory Thorsten Altenkirch Department of Informatics University of Munich Oettingenstr. 67, 80538 München, Germany, alti@informatik.uni-muenchen.de Abstract We
Extensional Equality in Intensional Type Theory Thorsten Altenkirch Department of Informatics University of Munich Oettingenstr. 67, 80538 München, Germany, alti@informatik.uni-muenchen.de Abstract We
Nominal Techniques in Isabelle/HOL
 Noname manuscript No. (will be inserted by the editor) Nominal Techniques in Isabelle/HOL Christian Urban Received: date / Accepted: date Abstract This paper describes a formalisation of the lambda-calculus
Noname manuscript No. (will be inserted by the editor) Nominal Techniques in Isabelle/HOL Christian Urban Received: date / Accepted: date Abstract This paper describes a formalisation of the lambda-calculus
Implementing Domain Specific Languages using Dependent Types and Partial Evaluation
 Implementing Domain Specific Languages using Dependent Types and Partial Evaluation Edwin Brady eb@cs.st-andrews.ac.uk University of St Andrews EE-PigWeek, January 7th 2010 EE-PigWeek, January 7th 2010
Implementing Domain Specific Languages using Dependent Types and Partial Evaluation Edwin Brady eb@cs.st-andrews.ac.uk University of St Andrews EE-PigWeek, January 7th 2010 EE-PigWeek, January 7th 2010
Two-Way Equational Tree Automata for AC-like Theories: Decidability and Closure Properties
 Two-Way Equational Tree Automata for AC-like Theories: Decidability and Closure Properties Kumar Neeraj Verma LSV/CNRS UMR 8643 & INRIA Futurs projet SECSI & ENS Cachan, France verma@lsv.ens-cachan.fr
Two-Way Equational Tree Automata for AC-like Theories: Decidability and Closure Properties Kumar Neeraj Verma LSV/CNRS UMR 8643 & INRIA Futurs projet SECSI & ENS Cachan, France verma@lsv.ens-cachan.fr
ÈÖÓÚ Ò Ò ÁÑÔÐ Ø ÓÒ È É Ï Ö Ø ÐÓÓ Ø Û Ý ØÓ ÔÖÓÚ Ø Ø Ñ ÒØ Ó Ø ÓÖÑ Á È Ø Ò É ÓÖ È É Ì ÓÐÐÓÛ Ò ÔÖÓÓ ØÝÔ Ò Ð Ó Ù ØÓ ÔÖÓÚ Ø Ø Ñ ÒØ Ó Ø ÓÖÑ Ü È Üµ É Üµµ Ý ÔÔ
 Å Ø Ó Ó ÈÖÓÓ ÊÙÐ Ó ÁÒ Ö Ò ¹ Ø ØÖÙØÙÖ Ó ÔÖÓÓ ÆÓÛ ËØÖ Ø ÓÖ ÓÒ ØÖÙØ Ò ÔÖÓÓ ÁÒØÖÓ ÙØ ÓÒ ØÓ ÓÑÑÓÒ ÔÖÓÓ Ø Ò ÕÙ Ê ÐÐ Ø Ø Ñ ÒØ ÒØ Ò Ø Ø Ø Ö ØÖÙ ÓÖ Ð º Ò Ø ÓÒ ÔÖÓÓ ÓÒÚ Ò Ò Ö ÙÑ ÒØ Ø Ø Ø Ø Ñ ÒØ ØÖÙ º ÆÓØ Ï ÒÒÓØ
Å Ø Ó Ó ÈÖÓÓ ÊÙÐ Ó ÁÒ Ö Ò ¹ Ø ØÖÙØÙÖ Ó ÔÖÓÓ ÆÓÛ ËØÖ Ø ÓÖ ÓÒ ØÖÙØ Ò ÔÖÓÓ ÁÒØÖÓ ÙØ ÓÒ ØÓ ÓÑÑÓÒ ÔÖÓÓ Ø Ò ÕÙ Ê ÐÐ Ø Ø Ñ ÒØ ÒØ Ò Ø Ø Ø Ö ØÖÙ ÓÖ Ð º Ò Ø ÓÒ ÔÖÓÓ ÓÒÚ Ò Ò Ö ÙÑ ÒØ Ø Ø Ø Ø Ñ ÒØ ØÖÙ º ÆÓØ Ï ÒÒÓØ
MSR, Access Control, and the Most Powerful Attacker
 MSR, Access Control, and the Most Powerful Attacker Iliano Cervesato Advanced Engineering and Sciences Division ITT Industries, Inc. 2560 Huntington Avenue, Alexandria, VA 22303-1410 USA Tel.: +1-202-404-4909,
MSR, Access Control, and the Most Powerful Attacker Iliano Cervesato Advanced Engineering and Sciences Division ITT Industries, Inc. 2560 Huntington Avenue, Alexandria, VA 22303-1410 USA Tel.: +1-202-404-4909,
Decomposition and Complexity of Hereditary History Preserving Bisimulation on BPP
 Decomposition and Complexity of Hereditary History Preserving Bisimulation on BPP Sibylle Fröschle and Sławomir Lasota Institute of Informatics, Warsaw University 02 097 Warszawa, Banacha 2, Poland sib,sl
Decomposition and Complexity of Hereditary History Preserving Bisimulation on BPP Sibylle Fröschle and Sławomir Lasota Institute of Informatics, Warsaw University 02 097 Warszawa, Banacha 2, Poland sib,sl
A Calculus for End-to-end Statistical Service Guarantees
 A Calculus for End-to-end Statistical Service Guarantees Technical Report: University of Virginia, CS-2001-19 (2nd revised version) Almut Burchard Ý Jörg Liebeherr Stephen Patek Ý Department of Mathematics
A Calculus for End-to-end Statistical Service Guarantees Technical Report: University of Virginia, CS-2001-19 (2nd revised version) Almut Burchard Ý Jörg Liebeherr Stephen Patek Ý Department of Mathematics
Refinement in Requirements Specification and Analysis: a Case Study
 Refinement in Requirements Specification and Analysis: a Case Study Edwin de Jong Hollandse Signaalapparaten P.O. Box 42 7550 GD Hengelo The Netherlands edejong@signaal.nl Jaco van de Pol CWI P.O. Box
Refinement in Requirements Specification and Analysis: a Case Study Edwin de Jong Hollandse Signaalapparaten P.O. Box 42 7550 GD Hengelo The Netherlands edejong@signaal.nl Jaco van de Pol CWI P.O. Box
Event Based Sequential Program Development: Application to Constructing a Pointer Program
 Event Based Sequential Program Development: Application to Constructing a Pointer Program Jean-Raymond Abrial Consultant, Marseille, France jr@abrial.org Abstract. In this article, I present an event approach
Event Based Sequential Program Development: Application to Constructing a Pointer Program Jean-Raymond Abrial Consultant, Marseille, France jr@abrial.org Abstract. In this article, I present an event approach
Deadlock. deadlock analysis - primitive processes, parallel composition, avoidance
 Deadlock CDS News: Brainy IBM Chip Packs One Million Neuron Punch Overview: ideas, 4 four necessary and sufficient conditions deadlock analysis - primitive processes, parallel composition, avoidance the
Deadlock CDS News: Brainy IBM Chip Packs One Million Neuron Punch Overview: ideas, 4 four necessary and sufficient conditions deadlock analysis - primitive processes, parallel composition, avoidance the
A Formal Architecture for the 3APL Agent Programming Language
 A Formal Architecture for the 3APL Agent Programming Language Mark d Inverno, Koen Hindriks Ý, and Michael Luck Þ Ý Þ Cavendish School of Computer Science, 115 New Cavendish Street, University of Westminster,
A Formal Architecture for the 3APL Agent Programming Language Mark d Inverno, Koen Hindriks Ý, and Michael Luck Þ Ý Þ Cavendish School of Computer Science, 115 New Cavendish Street, University of Westminster,
solutions:, and it cannot be the case that a supersolution is always greater than or equal to a subsolution.
 Chapter 4 Comparison The basic problem to be considered here is the question when one can say that a supersolution is always greater than or equal to a subsolution of a problem, where one in most cases
Chapter 4 Comparison The basic problem to be considered here is the question when one can say that a supersolution is always greater than or equal to a subsolution of a problem, where one in most cases
Improved Boosting Algorithms Using Confidence-rated Predictions
 Improved Boosting Algorithms Using Confidence-rated Predictions ÊÇÊÌ º ËÀÈÁÊ schapire@research.att.com AT&T Labs, Shannon Laboratory, 18 Park Avenue, Room A279, Florham Park, NJ 7932-971 ÇÊÅ ËÁÆÊ singer@research.att.com
Improved Boosting Algorithms Using Confidence-rated Predictions ÊÇÊÌ º ËÀÈÁÊ schapire@research.att.com AT&T Labs, Shannon Laboratory, 18 Park Avenue, Room A279, Florham Park, NJ 7932-971 ÇÊÅ ËÁÆÊ singer@research.att.com
ÙÒØ ÓÒ Ò Ø ÓÒ ÙÒØ ÓÒ ÖÓÑ ØÓ ÒÓØ Ö Ð Ø ÓÒ ÖÓÑ ØÓ Ù Ø Ø ÓÖ Ú ÖÝ Ü ¾ Ø Ö ÓÑ Ý ¾ Ù Ø Ø Ü Ýµ Ò Ø Ö Ð Ø ÓÒ Ò Ü Ýµ Ò Ü Þµ Ö Ò Ø Ö Ð Ø ÓÒ Ø Ò Ý Þº ÆÓØ Ø ÓÒ Á
 ÙÒØ ÓÒ Ò Ø ÓÒ ÙÒØ ÓÒ ÖÓÑ ØÓ ÒÓØ Ö Ð Ø ÓÒ ÖÓÑ ØÓ Ù Ø Ø ÓÖ Ú ÖÝ Ü ¾ Ø Ö ÓÑ Ý ¾ Ù Ø Ø Ü Ýµ Ò Ø Ö Ð Ø ÓÒ Ò Ü Ýµ Ò Ü Þµ Ö Ò Ø Ö Ð Ø ÓÒ Ø Ò Ý Þº ÆÓØ Ø ÓÒ Á Ü Ýµ Ò Ø Ö Ð Ø ÓÒ Û ÛÖ Ø Üµ ݺ Ì Ø Ø ÓÑ Ò Ó Ø ÙÒØ ÓÒ
ÙÒØ ÓÒ Ò Ø ÓÒ ÙÒØ ÓÒ ÖÓÑ ØÓ ÒÓØ Ö Ð Ø ÓÒ ÖÓÑ ØÓ Ù Ø Ø ÓÖ Ú ÖÝ Ü ¾ Ø Ö ÓÑ Ý ¾ Ù Ø Ø Ü Ýµ Ò Ø Ö Ð Ø ÓÒ Ò Ü Ýµ Ò Ü Þµ Ö Ò Ø Ö Ð Ø ÓÒ Ø Ò Ý Þº ÆÓØ Ø ÓÒ Á Ü Ýµ Ò Ø Ö Ð Ø ÓÒ Û ÛÖ Ø Üµ ݺ Ì Ø Ø ÓÑ Ò Ó Ø ÙÒØ ÓÒ
ishares Core Composite Bond ETF
 ishares Core Composite Bond ETF ARSN 154 626 767 ANNUAL FINANCIAL REPORT 30 June 2017 BlackRock Investment Management (Australia) Limited 13 006 165 975 Australian Financial Services Licence No 230523
ishares Core Composite Bond ETF ARSN 154 626 767 ANNUAL FINANCIAL REPORT 30 June 2017 BlackRock Investment Management (Australia) Limited 13 006 165 975 Australian Financial Services Licence No 230523
Liveness: The Readers / Writers Problem
 Liveness: The Readers / Writers Problem Admin stuff: Minute paper for concurrency revision lecture Please take one, fill out in 1st 5min & return to box at front by end of lecture Labs week 4 review: event
Liveness: The Readers / Writers Problem Admin stuff: Minute paper for concurrency revision lecture Please take one, fill out in 1st 5min & return to box at front by end of lecture Labs week 4 review: event
Domain, Range, Inverse
 Ê Ð Ø ÓÒ Ò Ø ÓÒ Ò ÖÝ Ö Ð Ø ÓÒ ÓÒ Ø Ò Ù Ø Ó Ü º Ì Ø ÒÝ Ê Ò ÖÝ Ö Ð Ø ÓÒº Ù Ø Ó ¾ Ü Ò ÖÝ Ö Ð Ø ÓÒ ÓÒ º ÆÓØ Ø ÓÒ Á µ ¾ Ê Û Ó Ø Ò ÛÖ Ø Ê º Ü ÑÔÐ Ò Ò ÖÝ Ö Ð Ø ÓÒ È ÓÒ ÓÖ ÐÐ Ñ Òµ ¾ ÑÈÒ Ñ Ò Ú Òº ËÓ È¾ È ¹ µ Ƚº
Ê Ð Ø ÓÒ Ò Ø ÓÒ Ò ÖÝ Ö Ð Ø ÓÒ ÓÒ Ø Ò Ù Ø Ó Ü º Ì Ø ÒÝ Ê Ò ÖÝ Ö Ð Ø ÓÒº Ù Ø Ó ¾ Ü Ò ÖÝ Ö Ð Ø ÓÒ ÓÒ º ÆÓØ Ø ÓÒ Á µ ¾ Ê Û Ó Ø Ò ÛÖ Ø Ê º Ü ÑÔÐ Ò Ò ÖÝ Ö Ð Ø ÓÒ È ÓÒ ÓÖ ÐÐ Ñ Òµ ¾ ÑÈÒ Ñ Ò Ú Òº ËÓ È¾ È ¹ µ Ƚº
38050 Povo (Trento), Italy Tel.: Fax: e mail: url:
 CENTRO PER LA RICERCA SCIENTIFICA E TECNOLOGICA 38050 Povo (Trento), Italy Tel.: +39 0461 314312 Fax: +39 0461 302040 e mail: prdoc@itc.it url: http://www.itc.it HISTORY DEPENDENT AUTOMATA Montanari U.,
CENTRO PER LA RICERCA SCIENTIFICA E TECNOLOGICA 38050 Povo (Trento), Italy Tel.: +39 0461 314312 Fax: +39 0461 302040 e mail: prdoc@itc.it url: http://www.itc.it HISTORY DEPENDENT AUTOMATA Montanari U.,
½ Ê Ú Û Ó ÆÒ ÕÙÓØ ÒØ ¾ ÇÖØ Ó ÓÒ Ð ÒÚ Ö ÒØ ÓÙ Ð Ö Ø ÓÒ Ý ÕÙÓØ ÒØ Ñ Ô ÇÖ Ø ÓÖÖ ÔÓÒ Ò Ü ÑÔÐ Ó ÓÖ Ø ÓÖÖ ÔÓÒ Ò Ü ÑÔÐ Ø Ò ÓÖ ÔÖÓ ÙØ Ü ÑÔÐ ÓÒØÖ Ø ÓÒ Ñ Ô ÇÔ Ò
 ÆÒ ÕÙÓØ ÒØ Ò Ø ÓÖÖ ÔÓÒ Ò Ó ÓÖ Ø ÃÝÓ Æ Ý Ñ Ö Ù Ø Ë ÓÓÐ Ó Ë Ò ÃÝÓØÓ ÍÒ Ú Ö ØÝ ÁÒØ ÖÒ Ø ÓÒ Ð ÓÒ Ö Ò ÓÒ Ê ÒØ Ú Ò Ò Å Ø Ñ Ø Ò Ø ÔÔÐ Ø ÓÒ º Ë ÔØ Ñ Ö ¾ ß ¼ ¾¼¼ µ Ô ÖØÑ ÒØ Ó Å Ø Ñ Ø ÃÍ ÈÓ Ø Ö Ù Ø ÒØ Ö Ð ÙÑ Ã ÖÒ
ÆÒ ÕÙÓØ ÒØ Ò Ø ÓÖÖ ÔÓÒ Ò Ó ÓÖ Ø ÃÝÓ Æ Ý Ñ Ö Ù Ø Ë ÓÓÐ Ó Ë Ò ÃÝÓØÓ ÍÒ Ú Ö ØÝ ÁÒØ ÖÒ Ø ÓÒ Ð ÓÒ Ö Ò ÓÒ Ê ÒØ Ú Ò Ò Å Ø Ñ Ø Ò Ø ÔÔÐ Ø ÓÒ º Ë ÔØ Ñ Ö ¾ ß ¼ ¾¼¼ µ Ô ÖØÑ ÒØ Ó Å Ø Ñ Ø ÃÍ ÈÓ Ø Ö Ù Ø ÒØ Ö Ð ÙÑ Ã ÖÒ
ÁÒ ÙØ Ú ¹ ÙØ Ú ËÝ Ø Ñ Ñ Ø Ñ Ø Ð ÐÓ Ò Ø Ø Ø Ð Ð ÖÒ Ò Ô Ö Ô Ø Ú Æ ÓÐ ÓØ Å Ð Ë Ø ÇÐ Ú Ö Ì ÝØ Ù ÍÒ Ú Ö Ø È Ö ¹ËÙ ÆÊË ÁÆÊÁ ÈÖÓ ¾¼¼
 ÁÒ ÙØ Ú ¹ ÙØ Ú ËÝ Ø Ñ Ñ Ø Ñ Ø Ð ÐÓ Ò Ø Ø Ø Ð Ð ÖÒ Ò Ô Ö Ô Ø Ú Æ ÓÐ ÓØ Å Ð Ë Ø ÇÐ Ú Ö Ì ÝØ Ù ÍÒ Ú Ö Ø È Ö ¹ËÙ ÆÊË ÁÆÊÁ ÈÖÓ ¾¼¼ Ó ÜÔ ÖØ Ð ÒØ ÒØ Ø Ò Ò Öº º º µ Ý ÖÑ ÐÓ¹ Ö Ò Ð ÓÐ Ó Ø Ø ÓÖ Ñ Ð Ð ÓÐ Ï Ø Ó ÝÓÙ
ÁÒ ÙØ Ú ¹ ÙØ Ú ËÝ Ø Ñ Ñ Ø Ñ Ø Ð ÐÓ Ò Ø Ø Ø Ð Ð ÖÒ Ò Ô Ö Ô Ø Ú Æ ÓÐ ÓØ Å Ð Ë Ø ÇÐ Ú Ö Ì ÝØ Ù ÍÒ Ú Ö Ø È Ö ¹ËÙ ÆÊË ÁÆÊÁ ÈÖÓ ¾¼¼ Ó ÜÔ ÖØ Ð ÒØ ÒØ Ø Ò Ò Öº º º µ Ý ÖÑ ÐÓ¹ Ö Ò Ð ÓÐ Ó Ø Ø ÓÖ Ñ Ð Ð ÓÐ Ï Ø Ó ÝÓÙ
x = x 1x 2 x (p-1)x x = 3 x = 3 x = 3 x = 3 0 x 1 x 2 x... (p-1)x
 ÌÖ Ò ÓÖÑ Ø ÓÒ Ô Ö ÐÐ Ð ÔÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ Ô Ö ÐÐ Ð Þ Ø ÓÒ Ø Ò ÕÙ º ½º ÈÖÓ Ö Ñ Å ÔÔ Ò ÈÖÓ Ö Ñ È ÖØ Ø ÓÒ Ò º Ô Ò Ò Ò ÐÝ º Ë ÙÐ Ò ÄÓ Ð Ò Ò º Ó ØÖ ÙØ ÓÒº ¾º Ø Å ÔÔ Ò º Ø Ô ÖØ Ø ÓÒ Ò º ÓÑÑÙÒ Ø ÓÒ ØÛ Ò ÔÖÓ ÓÖ
ÌÖ Ò ÓÖÑ Ø ÓÒ Ô Ö ÐÐ Ð ÔÖÓ Ö ÑÑ Ò ÈÖÓ Ö Ñ Ô Ö ÐÐ Ð Þ Ø ÓÒ Ø Ò ÕÙ º ½º ÈÖÓ Ö Ñ Å ÔÔ Ò ÈÖÓ Ö Ñ È ÖØ Ø ÓÒ Ò º Ô Ò Ò Ò ÐÝ º Ë ÙÐ Ò ÄÓ Ð Ò Ò º Ó ØÖ ÙØ ÓÒº ¾º Ø Å ÔÔ Ò º Ø Ô ÖØ Ø ÓÒ Ò º ÓÑÑÙÒ Ø ÓÒ ØÛ Ò ÔÖÓ ÓÖ
Tensor. Field. Vector 2D Length. SI BG cgs. Tensor. Units. Template. DOFs u v. Distribution Functions. Domain
 ÁÒØÖÓ ÙØ ÓÒ ØÓ Ø ÁÌ ÈË Ð ÁÒØ Ö ÖÐ ÇÐÐ Ú Ö¹ ÓÓ Ì ÍÒ Ú Ö ØÝ Ó Ö Ø ÓÐÙÑ Å Ö Å ÐÐ Ö Ä ÛÖ Ò Ä Ú ÖÑÓÖ Æ Ø ÓÒ Ð Ä ÓÖ ØÓÖÝ Ò Ð ÐÓÒ Ö Ê Ò Ð Ö ÈÓÐÝØ Ò ÁÒ Ø ØÙØ ¾¼½½ ËÁ Å Ë ÓÒ Ö Ò Ê ÒÓ Æ Ú Å Ö ¾¼½½ ÇÐÐ Ú Ö¹ ÓÓ Å
ÁÒØÖÓ ÙØ ÓÒ ØÓ Ø ÁÌ ÈË Ð ÁÒØ Ö ÖÐ ÇÐÐ Ú Ö¹ ÓÓ Ì ÍÒ Ú Ö ØÝ Ó Ö Ø ÓÐÙÑ Å Ö Å ÐÐ Ö Ä ÛÖ Ò Ä Ú ÖÑÓÖ Æ Ø ÓÒ Ð Ä ÓÖ ØÓÖÝ Ò Ð ÐÓÒ Ö Ê Ò Ð Ö ÈÓÐÝØ Ò ÁÒ Ø ØÙØ ¾¼½½ ËÁ Å Ë ÓÒ Ö Ò Ê ÒÓ Æ Ú Å Ö ¾¼½½ ÇÐÐ Ú Ö¹ ÓÓ Å
How hard is it to control sequential elections via the agenda?
 How hard is it to control sequential elections via the agenda? Vincent Conitzer Department of Computer Science Duke University Durham, NC 27708, USA conitzer@cs.duke.edu Jérôme Lang LAMSADE Université
How hard is it to control sequential elections via the agenda? Vincent Conitzer Department of Computer Science Duke University Durham, NC 27708, USA conitzer@cs.duke.edu Jérôme Lang LAMSADE Université
½º»¾¼ º»¾¼ ¾º»¾¼ º»¾¼ º»¾¼ º»¾¼ º»¾¼ º»¾¼» ¼» ¼ ÌÓØ Ð»½ ¼
 Ò Ð Ü Ñ Ò Ø ÓÒ ËÌ ½½ ÈÖÓ Ð ØÝ ² Å ÙÖ Ì ÓÖÝ ÌÙ Ý ¾¼½ ½¼ ¼¼ Ñ ß ½¾ ¼¼Ò Ì ÐÓ ¹ ÓÓ Ü Ñ Ò Ø ÓÒº ÓÙ Ñ Ý Ù Ø Ó ÔÖ Ô Ö ÒÓØ ÝÓÙ Û ÙØ ÝÓÙ Ñ Ý ÒÓØ Ö Ñ Ø Ö Ð º Á ÕÙ Ø ÓÒ Ñ Ñ ÙÓÙ ÓÖ ÓÒ Ù Ò ÔÐ Ñ ØÓ Ð Ö Ý Øº ÍÒÐ ÔÖÓ
Ò Ð Ü Ñ Ò Ø ÓÒ ËÌ ½½ ÈÖÓ Ð ØÝ ² Å ÙÖ Ì ÓÖÝ ÌÙ Ý ¾¼½ ½¼ ¼¼ Ñ ß ½¾ ¼¼Ò Ì ÐÓ ¹ ÓÓ Ü Ñ Ò Ø ÓÒº ÓÙ Ñ Ý Ù Ø Ó ÔÖ Ô Ö ÒÓØ ÝÓÙ Û ÙØ ÝÓÙ Ñ Ý ÒÓØ Ö Ñ Ø Ö Ð º Á ÕÙ Ø ÓÒ Ñ Ñ ÙÓÙ ÓÖ ÓÒ Ù Ò ÔÐ Ñ ØÓ Ð Ö Ý Øº ÍÒÐ ÔÖÓ
Proof a n d Com p uta tion in Coq Maxime Dénès, Benjamin Grégoire, Chantal Keller, Pierre Yves Strub, Laurent Théry Map 16 p.1
 ÈÖÓÓ Ò ÓÑÔÙØ Ø ÓÒ Ò ÓÕ Å Ü Ñ Ò Ò Ñ Ò Ö Ó Ö ÒØ Ð Ã ÐÐ Ö È ÖÖ Ú ËØÖÙ Ä ÙÖ ÒØ Ì ÖÝ Map 16 p.1 ÅÓØ Ú Ø ÓÒ ÔÖÓ Ö ÑÑ Ò Ð Ò Ù ÙÒØ ÓÒ Ð Compute prime 31. = true ÔÖÓÚ Ö Ì ÓÖ Ñ Check Euclid_dvdX. forall m n p :
ÈÖÓÓ Ò ÓÑÔÙØ Ø ÓÒ Ò ÓÕ Å Ü Ñ Ò Ò Ñ Ò Ö Ó Ö ÒØ Ð Ã ÐÐ Ö È ÖÖ Ú ËØÖÙ Ä ÙÖ ÒØ Ì ÖÝ Map 16 p.1 ÅÓØ Ú Ø ÓÒ ÔÖÓ Ö ÑÑ Ò Ð Ò Ù ÙÒØ ÓÒ Ð Compute prime 31. = true ÔÖÓÚ Ö Ì ÓÖ Ñ Check Euclid_dvdX. forall m n p :
Ë ÁÌÇ ÌÓ Ó ÍÒ Ú Ö Øݵ Ç ¼ Ô Û Ö ÙÒÓ Ø Ò Ð Ä Ò ÙÖ ÖÝ ÓÒ ÒÓØ Ý ÛÓÖ Û Ø Ã ÞÙ ÖÓ Á Ö Ó ÒØ Ë Ò ÝÓ ÍÒ Ú Ö Øݵ Ç
 Ë ÁÌÇ ÌÓ Ó ÍÒ Ú Ö Øݵ Ç ¼ Ô Û Ö ÙÒÓ Ø Ò Ð Ä Ò ÙÖ ÖÝ ÓÒ ÒÓØ Ý ÛÓÖ Û Ø Ã ÞÙ ÖÓ Á Ö Ó ÒØ Ë Ò ÝÓ ÍÒ Ú Ö Øݵ Ç ½ Ä Ò Ô Ô Ä Ô Õµ Ø ¹Ñ Ò ÓÐ Ó Ø Ò Ý Ä Ò ÓÒ Ø ØÖ Ú Ð ÒÓØ Ò Ë º Ô Õ¹ ÙÖ ÖÝ Ô Õµ¹ÙÖÚ ¾ ÈÖÓ Ð Ñ Ø Ð
Ë ÁÌÇ ÌÓ Ó ÍÒ Ú Ö Øݵ Ç ¼ Ô Û Ö ÙÒÓ Ø Ò Ð Ä Ò ÙÖ ÖÝ ÓÒ ÒÓØ Ý ÛÓÖ Û Ø Ã ÞÙ ÖÓ Á Ö Ó ÒØ Ë Ò ÝÓ ÍÒ Ú Ö Øݵ Ç ½ Ä Ò Ô Ô Ä Ô Õµ Ø ¹Ñ Ò ÓÐ Ó Ø Ò Ý Ä Ò ÓÒ Ø ØÖ Ú Ð ÒÓØ Ò Ë º Ô Õ¹ ÙÖ ÖÝ Ô Õµ¹ÙÖÚ ¾ ÈÖÓ Ð Ñ Ø Ð
Ó Ú ÐÙ Ö ÒÚÓÐÚ Ò ÖØ Ò Ô ÖØ Ó Ø ÔÖÓ Ö Ñµ Ò ØÓ ÐÔ Ø Ø ÔÖÓ Ö ÑÑ Ö Ñ Ø º ÁÒ Ø Ø ÐÐÝ ØÝÔ Ð Ò Ù Ø ØÝÔ Ö ÒÓØ Ò ÓÑ Ø Ò Ø Ø Ø Ô ÖØ Ò ÓÑÔÙØ Ø ÓÒ ÙØ Ö Ø Ö ÓÑ Ø Ò
 ÙÒ Û Ø ÙÒØ ÓÒ Ð Ô Ò Ò ÓÖ Ö Øµ ÌÝÔ Î ÐÙ Ò ËØ Ø ÓÑÔÙØ Ø ÓÒ Ò À ÐÐ Ì ÓÑ À ÐÐ Ö Ò Ñ Ö ¾ ¾¼¼¼ ØÖ Ø Ì Ô Ô Ö ÐÐÙ ØÖ Ø ÓÛ À Ðг ØÝÔ Ð Ý Ø Ñ Ò Ù ØÓ ÜÔÖ ÓÑÔÙØ Ø ÓÒ º Ë Ò ÓÑÔÙØ Ø ÓÒ ÓÒ Ø ØÝÔ Ð Ú Ð Ö Ô Ö ÓÖÑ Ý Ø ØÝÔ
ÙÒ Û Ø ÙÒØ ÓÒ Ð Ô Ò Ò ÓÖ Ö Øµ ÌÝÔ Î ÐÙ Ò ËØ Ø ÓÑÔÙØ Ø ÓÒ Ò À ÐÐ Ì ÓÑ À ÐÐ Ö Ò Ñ Ö ¾ ¾¼¼¼ ØÖ Ø Ì Ô Ô Ö ÐÐÙ ØÖ Ø ÓÛ À Ðг ØÝÔ Ð Ý Ø Ñ Ò Ù ØÓ ÜÔÖ ÓÑÔÙØ Ø ÓÒ º Ë Ò ÓÑÔÙØ Ø ÓÒ ÓÒ Ø ØÝÔ Ð Ú Ð Ö Ô Ö ÓÖÑ Ý Ø ØÝÔ
Computational Inelasticity FHLN05. Assignment A non-linear elasto-plastic problem
 Computational Inelasticity FHLN05 Assignment 2016 A non-linear elasto-plastic problem General instructions A written report should be submitted to the Division of Solid Mechanics no later than 1 November
Computational Inelasticity FHLN05 Assignment 2016 A non-linear elasto-plastic problem General instructions A written report should be submitted to the Division of Solid Mechanics no later than 1 November
Optimized Lookahead Trees: Extensions to Large and Continuous Action Spaces
 Optimized Lookahead Trees: Extensions to Large and Continuous Action Spaces Tobias Jung, Damien Ernst, and Francis Maes Montefiore Institute University of Liège {tjung}@ulg.ac.be Motto: Bridging the gap
Optimized Lookahead Trees: Extensions to Large and Continuous Action Spaces Tobias Jung, Damien Ernst, and Francis Maes Montefiore Institute University of Liège {tjung}@ulg.ac.be Motto: Bridging the gap
M 1 M 2 M 3 M 1 M 1 M 1 M 2 M 3 M 3
 ÅË ØÖ ÙØ ÔØ Ú Å Ø ÙÖ Ø Ë Ð Ø ÓÒ Ç ¾¼½½ Ù Ð Ò Ð Ð Ö Ð ½ Ë Ø Ò Î Ö Ð ½,¾ ½ ÁÆÊÁ Ä ÐÐ ¹ÆÓÖ ÙÖÓÔ ÍÒ Ú Ö Ø Ä ÐÐ ½ ¾ ÍÒ Ú Ö Ø Æ ËÓÔ ÒØ ÔÓÐ Ö Ò ØØÔ»»ÛÛÛº ºÙÒ º Ö» Ú Ö Ð ÂÙÐÝ ½ ¾¼½½ ½»½ ÈÓ Ø ÓÒ Ó Ø ÛÓÖ ÇÒ Ý ÔÓ
ÅË ØÖ ÙØ ÔØ Ú Å Ø ÙÖ Ø Ë Ð Ø ÓÒ Ç ¾¼½½ Ù Ð Ò Ð Ð Ö Ð ½ Ë Ø Ò Î Ö Ð ½,¾ ½ ÁÆÊÁ Ä ÐÐ ¹ÆÓÖ ÙÖÓÔ ÍÒ Ú Ö Ø Ä ÐÐ ½ ¾ ÍÒ Ú Ö Ø Æ ËÓÔ ÒØ ÔÓÐ Ö Ò ØØÔ»»ÛÛÛº ºÙÒ º Ö» Ú Ö Ð ÂÙÐÝ ½ ¾¼½½ ½»½ ÈÓ Ø ÓÒ Ó Ø ÛÓÖ ÇÒ Ý ÔÓ
È Ö Ø ² ÑÔ Ö Ø Ò ÓÖÑ Ø ÓÒ ÓÖ Ñ È Ö Ø Ò ÓÖÑ Ø ÓÒ ÈÐ Ý Ö ÒÓÛ ÓÙØ Ø ÔÖ Ú ÓÙ ÑÓÚ Ó ÓÔÔÓÒ ÒØ º º º Ð ¹ËØ Û ÖØ Ñ º ÁÑÔ Ö Ø Ò ÓÖÑ Ø ÓÒ ÈÐ Ý Ö Ó ÒÓØ ÒÓÛ ÓÙØ Û
 Ð ¹ËØ Û ÖØ Ñ Ò Ð Û ÐÐ Ñ Ù Á Ñ ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ö Ð Ýµ ½ Ø Ó Å Ý ¾¼½¾ È Ö Ø ² ÑÔ Ö Ø Ò ÓÖÑ Ø ÓÒ ÓÖ Ñ È Ö Ø Ò ÓÖÑ Ø ÓÒ ÈÐ Ý Ö ÒÓÛ ÓÙØ Ø ÔÖ Ú ÓÙ ÑÓÚ Ó ÓÔÔÓÒ ÒØ º º º Ð ¹ËØ Û ÖØ Ñ º ÁÑÔ Ö Ø Ò ÓÖÑ Ø ÓÒ ÈÐ
Ð ¹ËØ Û ÖØ Ñ Ò Ð Û ÐÐ Ñ Ù Á Ñ ÍÒ Ú Ö ØÝ Ó Ð ÓÖÒ Ö Ð Ýµ ½ Ø Ó Å Ý ¾¼½¾ È Ö Ø ² ÑÔ Ö Ø Ò ÓÖÑ Ø ÓÒ ÓÖ Ñ È Ö Ø Ò ÓÖÑ Ø ÓÒ ÈÐ Ý Ö ÒÓÛ ÓÙØ Ø ÔÖ Ú ÓÙ ÑÓÚ Ó ÓÔÔÓÒ ÒØ º º º Ð ¹ËØ Û ÖØ Ñ º ÁÑÔ Ö Ø Ò ÓÖÑ Ø ÓÒ ÈÐ
É ÀÓÛ Ó Ý Ò ² Ö Ò ÁÒ Ö Ò «Ö ÓØ ÑÔ Ù ÔÖÓ Ð ØÝ ØÓ Ö ÙÒ ÖØ ÒØÝ ÙØ Ø Ý ÓÒ Ø ÓÒ ÓÒ «Ö ÒØ Ø Ò º Ü ÑÔÐ ÁÑ Ò Ð Ò Ð ØÖ Ð Û Ø Ò ½ Ñ Ø Ô Ö Ó Ù Ø º ÁÒ Ô Ö ÓÒ Ù Ø
 ËØ Ø Ø Ð È Ö Ñ Ý Ò ² Ö ÕÙ ÒØ Ø ÊÓ ÖØ Ä ÏÓÐÔ ÖØ Ù ÍÒ Ú Ö ØÝ Ô ÖØÑ ÒØ Ó ËØ Ø Ø Ð Ë Ò ¾¼½ Ë Ô ½¼ ÈÖÓ Ñ Ò Ö É ÀÓÛ Ó Ý Ò ² Ö Ò ÁÒ Ö Ò «Ö ÓØ ÑÔ Ù ÔÖÓ Ð ØÝ ØÓ Ö ÙÒ ÖØ ÒØÝ ÙØ Ø Ý ÓÒ Ø ÓÒ ÓÒ «Ö ÒØ Ø Ò º Ü ÑÔÐ ÁÑ
ËØ Ø Ø Ð È Ö Ñ Ý Ò ² Ö ÕÙ ÒØ Ø ÊÓ ÖØ Ä ÏÓÐÔ ÖØ Ù ÍÒ Ú Ö ØÝ Ô ÖØÑ ÒØ Ó ËØ Ø Ø Ð Ë Ò ¾¼½ Ë Ô ½¼ ÈÖÓ Ñ Ò Ö É ÀÓÛ Ó Ý Ò ² Ö Ò ÁÒ Ö Ò «Ö ÓØ ÑÔ Ù ÔÖÓ Ð ØÝ ØÓ Ö ÙÒ ÖØ ÒØÝ ÙØ Ø Ý ÓÒ Ø ÓÒ ÓÒ «Ö ÒØ Ø Ò º Ü ÑÔÐ ÁÑ
ËØ ÒÓ Ö Ô Ý ËØ ÒÓ Ö Ô Ý ÑÓ Ó ÓÚ ÖØ ÓÑÑÙÒ Ø ÓÒº Ñ Ñ Ñ Ñ ÓÚ Ö Ñ ( ) Ø Ó ÜØ( ) Ý ÒÒ Ð Û Ø Ô Ú Û Ö Ò Ý Ò Ö ÖºÚº ÓÒ X Ò Ø Ð Ñ ÓÖ Ü ÑÔÐ Ñ ( ) ÜØ( ) ººº Ñ Ò
 Å Ò Ñ Þ Ò Ø Ú ØÓÖØ ÓÒ ÙÒØ ÓÒ Û Ø ÆÓÒ¹ Ò ÖÝ Ñ Ò ÇÔ Ö Ø ÓÒ Ò ËØ ÒÓ Ö Ô Ý ÌÓÑ ÐÐ Ö Ò Â Ö Ö Ôغ Ó Ð ØÖ Ð Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ËÍÆ Ò ÑØÓÒ Æ Û ÓÖ Ë ÓÒ Á ÁÒØ ÖÒ Ø ÓÒ Ð ÏÓÖ ÓÔ ÓÒ ÁÒ ÓÖÑ Ø ÓÒ ÓÖ Ò Ò Ë ÙÖ ØÝ Ñ Ö ½
Å Ò Ñ Þ Ò Ø Ú ØÓÖØ ÓÒ ÙÒØ ÓÒ Û Ø ÆÓÒ¹ Ò ÖÝ Ñ Ò ÇÔ Ö Ø ÓÒ Ò ËØ ÒÓ Ö Ô Ý ÌÓÑ ÐÐ Ö Ò Â Ö Ö Ôغ Ó Ð ØÖ Ð Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ËÍÆ Ò ÑØÓÒ Æ Û ÓÖ Ë ÓÒ Á ÁÒØ ÖÒ Ø ÓÒ Ð ÏÓÖ ÓÔ ÓÒ ÁÒ ÓÖÑ Ø ÓÒ ÓÖ Ò Ò Ë ÙÖ ØÝ Ñ Ö ½
 Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ Ð ØÙÖ ÒØÖÓ Ù Ø ÖÓÙØ Ò ÔÖÓ Ð Ñ Ò Ö ÓÑÑÓÒ ÔÔÖÓ ØÓ Ø ÓÐÙØ ÓÒ Ì Ð ÓÖ Ø Ñµ ÓÖ ÓÖØ Ø¹Ô Ø ÖÓÙØ Ò º ØÖ ³ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¼ ÊÓÙØ Ò Å ØØ Û ÊÓÙ Ò
Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ Ð ØÙÖ ÒØÖÓ Ù Ø ÖÓÙØ Ò ÔÖÓ Ð Ñ Ò Ö ÓÑÑÓÒ ÔÔÖÓ ØÓ Ø ÓÐÙØ ÓÒ Ì Ð ÓÖ Ø Ñµ ÓÖ ÓÖØ Ø¹Ô Ø ÖÓÙØ Ò º ØÖ ³ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¼ ÊÓÙØ Ò Å ØØ Û ÊÓÙ Ò
ÇÙØÐ Ò Ó Ø Ø Ð ÅÓØ Ú Ø ÓÒ = ¾ ÙÔ Ö ÝÑÑ ØÖ Ò ¹Å ÐÐ ÕÙ ÒØÙÑ Ñ Ò ÆÙÑ Ö Ð Ð ÓÖ Ø Ñ Ò ÒÙÑ Ö Ð Ö ÙÐØ Ü Ø ÓÐÙØ ÓÒ ÙÖØ Ö Ô Ö Ô Ø Ú
 Ü Ø ÓÐÙØ ÓÒ Ò = ¾ ÙÔ Ö ÝÑÑ ØÖ Ò ¹Å ÐÐ ÕÙ ÒØÙÑ Ñ Ò Û Ø ËÍ( ) Ù ÖÓÙÔ Ò Ö Åº ËÑÓÐÙ ÓÛ ÁÒ Ø ØÙØ Ó È Ý Â ÐÐÓÒ Ò ÍÒ Ú Ö ØÝ ÄÁ Ö ÓÛ Ë ÓÓÐ Ó Ì ÓÖ Ø Ð È Ý ÇÙØÐ Ò Ó Ø Ø Ð ÅÓØ Ú Ø ÓÒ = ¾ ÙÔ Ö ÝÑÑ ØÖ Ò ¹Å ÐÐ ÕÙ ÒØÙÑ
Ü Ø ÓÐÙØ ÓÒ Ò = ¾ ÙÔ Ö ÝÑÑ ØÖ Ò ¹Å ÐÐ ÕÙ ÒØÙÑ Ñ Ò Û Ø ËÍ( ) Ù ÖÓÙÔ Ò Ö Åº ËÑÓÐÙ ÓÛ ÁÒ Ø ØÙØ Ó È Ý Â ÐÐÓÒ Ò ÍÒ Ú Ö ØÝ ÄÁ Ö ÓÛ Ë ÓÓÐ Ó Ì ÓÖ Ø Ð È Ý ÇÙØÐ Ò Ó Ø Ø Ð ÅÓØ Ú Ø ÓÒ = ¾ ÙÔ Ö ÝÑÑ ØÖ Ò ¹Å ÐÐ ÕÙ ÒØÙÑ
 Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ Ð ØÙÖ Ö ÓÑ ÓÑÑÓÒ Ò ØÛÓÖ ÓÔØ Ñ Þ Ø ÓÒ Ó Ð Ò ÓÒ ØÖ ÒØ Ò Û Ý Ì ÓÙÖº ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¼ Å ØØ Û ÊÓÙ Ò Æ ØÛÓÖ ÇÔØ Ñ Þ Ø ÓÒ
Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ Ð ØÙÖ Ö ÓÑ ÓÑÑÓÒ Ò ØÛÓÖ ÓÔØ Ñ Þ Ø ÓÒ Ó Ð Ò ÓÒ ØÖ ÒØ Ò Û Ý Ì ÓÙÖº ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¼ Å ØØ Û ÊÓÙ Ò Æ ØÛÓÖ ÇÔØ Ñ Þ Ø ÓÒ
From Argument Games to Persuasion Dialogues
 From Argument Games to Persuasion Dialogues Nicolas Maudet (aka Nicholas of Paris) 08/02/10 (DGHRCM workshop) LAMSADE Université Paris-Dauphine 1 / 33 Introduction Main sources of inspiration for this
From Argument Games to Persuasion Dialogues Nicolas Maudet (aka Nicholas of Paris) 08/02/10 (DGHRCM workshop) LAMSADE Université Paris-Dauphine 1 / 33 Introduction Main sources of inspiration for this
Many-Valued Logics. A Mathematical and Computational Introduction. Luis M. Augusto
 Many-Valued Logics A Mathematical and Computational Introduction Luis M. Augusto Individual author and College Publications 2017 All rights reserved. ISBN 978-1-84890-250-3 College Publications Scientific
Many-Valued Logics A Mathematical and Computational Introduction Luis M. Augusto Individual author and College Publications 2017 All rights reserved. ISBN 978-1-84890-250-3 College Publications Scientific
arxiv: v25 [math.ca] 21 Nov 2008
![arxiv: v25 [math.ca] 21 Nov 2008 arxiv: v25 [math.ca] 21 Nov 2008](/thumbs/75/71471955.jpg) ËÓÑ ÓÒ ØÙÖ ÓÒ Ø ÓÒ Ò ÑÙÐØ ÔÐ Ø ÓÒ Ó ÓÑÔÐ Ü Ö Ðµ ÒÙÑ Ö ÔÓÐÓÒ Ù Þ ÌÝ Þ arxiv:0807.3010v25 [math.ca] 21 Nov 2008 ØÖ Øº Ï Ù ÓÒ ØÙÖ Ö Ð Ø ØÓ Ø ÓÐÐÓÛ Ò ØÛÓ ÓÒ ØÙÖ Áµ µ ÓÖ ÓÑÔÐ Ü ÒÙÑ Ö x 1,...,x n Ø Ö Ü Ø Ö Ø
ËÓÑ ÓÒ ØÙÖ ÓÒ Ø ÓÒ Ò ÑÙÐØ ÔÐ Ø ÓÒ Ó ÓÑÔÐ Ü Ö Ðµ ÒÙÑ Ö ÔÓÐÓÒ Ù Þ ÌÝ Þ arxiv:0807.3010v25 [math.ca] 21 Nov 2008 ØÖ Øº Ï Ù ÓÒ ØÙÖ Ö Ð Ø ØÓ Ø ÓÐÐÓÛ Ò ØÛÓ ÓÒ ØÙÖ Áµ µ ÓÖ ÓÑÔÐ Ü ÒÙÑ Ö x 1,...,x n Ø Ö Ü Ø Ö Ø
Ì ÄÈ Ë ÈÖÓ Ð Ñ Ì ÄÈ Ë ÐÓÒ Ø Ô Ö Ñ Ø Ö Þ ÓÑÑÓÒ Ù ÕÙ Ò µ ÔÖÓ Ð Ñ Ò Ö Ð Þ Ø ÓÒ Ó Û ÐÐ ÒÓÛÒ Ä Ë ÔÖÓ Ð Ñ ÓÒØ Ò Ò Ô¹ÓÒ ØÖ ÒØ º Ò Ø ÓÒ ÁÒ ÄÈ Ë(,, Ã ½, Ã ¾, )
 Ð ÓÖ Ø Ñ ÓÖ ÓÑÔÙØ Ò Ø ÄÓÒ Ø È Ö Ñ Ø Ö Þ ÓÑÑÓÒ ËÙ ÕÙ Ò Ó Ø Ëº ÁÐ ÓÔÓÙÐÓ ½ Å Ö Ò ÃÙ ¾ ź ËÓ Ð Ê Ñ Ò ½ Ò ÌÓÑ Þ Ï Ð ¾ ½ Ð ÓÖ Ø Ñ Ò ÖÓÙÔ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Ã Ò ÓÐÐ ÄÓÒ ÓÒ ¾ ÙÐØÝ Ó Å Ø Ñ Ø ÁÒ ÓÖÑ Ø Ò ÔÔÐ
Ð ÓÖ Ø Ñ ÓÖ ÓÑÔÙØ Ò Ø ÄÓÒ Ø È Ö Ñ Ø Ö Þ ÓÑÑÓÒ ËÙ ÕÙ Ò Ó Ø Ëº ÁÐ ÓÔÓÙÐÓ ½ Å Ö Ò ÃÙ ¾ ź ËÓ Ð Ê Ñ Ò ½ Ò ÌÓÑ Þ Ï Ð ¾ ½ Ð ÓÖ Ø Ñ Ò ÖÓÙÔ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò Ã Ò ÓÐÐ ÄÓÒ ÓÒ ¾ ÙÐØÝ Ó Å Ø Ñ Ø ÁÒ ÓÖÑ Ø Ò ÔÔÐ
NS Ilist Clist F. F y<=w
 Î Ö Ø ÓÒ Ó Ç Ø¹ÓÖ ÒØ ÈÖÓ Ö Ñ ÖÓÑ Ö Ò Ô ØÓ ÝÒ Ñ Ö Ñ Ú Æ ÙÑ ÒÒ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ËØ Ú Ò ÁÒ Ø ØÙØ Ó Ì ÒÓÐÓ Ý È º º ÐÐ Ë ÓÓÐ ÓÒ ÄÓ Ò Ë Ñ ÒØ Ó ËØ Ø ÁÌ ÍÒ Ú Ö ØÝ ÓÔ Ò Ò ÇØÓ Ö ¾¼¼ È ÖØ ÐÐÝ ÙÔÔÓÖØ Ý ÍË ÆË
Î Ö Ø ÓÒ Ó Ç Ø¹ÓÖ ÒØ ÈÖÓ Ö Ñ ÖÓÑ Ö Ò Ô ØÓ ÝÒ Ñ Ö Ñ Ú Æ ÙÑ ÒÒ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ËØ Ú Ò ÁÒ Ø ØÙØ Ó Ì ÒÓÐÓ Ý È º º ÐÐ Ë ÓÓÐ ÓÒ ÄÓ Ò Ë Ñ ÒØ Ó ËØ Ø ÁÌ ÍÒ Ú Ö ØÝ ÓÔ Ò Ò ÇØÓ Ö ¾¼¼ È ÖØ ÐÐÝ ÙÔÔÓÖØ Ý ÍË ÆË
ÅÓ Ø Ü Ø Ò ÖÓ ¹ÓÚ Ö Ö ÓÙÖ ÔÖÓÚ ÓÒÐÝ ÐÐÓÛ Ö ÔÖ ÒØ Ø ÓÒ Ñ ÒØ ÇÚ ÖÚ Û ÛÓÖÐ ÔÔÐ Ø ÓÒ Ò Ö ÓÙÖ Û Ø Ö ÝÒØ Ø Ò ¹ Ê Ð Ö ÔÖ ÒØ Ø ÓÒ º Ñ ÒØ ÅÙ Ö Ö Ö ÔÖ ÒØ Ø ÓÒ Ö
 Ã ÔÔ Ö Ë ÙÐ Ö Ã Ö Ò ÔÔ ÖÐ Òº ºÙÔ ÒÒº Ù Î Ö Æ Ø ÜØ Ò ÓÒ Ò Ñ ÔÔ Ò ØÓ ÓØ Ö Ð Ü Ð Ö ÓÙÖ ÂÙÒ ¾ Ø ¾¼¼ ÅÓ Ø Ü Ø Ò ÖÓ ¹ÓÚ Ö Ö ÓÙÖ ÔÖÓÚ ÓÒÐÝ ÐÐÓÛ Ö ÔÖ ÒØ Ø ÓÒ Ñ ÒØ ÇÚ ÖÚ Û ÛÓÖÐ ÔÔÐ Ø ÓÒ Ò Ö ÓÙÖ Û Ø Ö ÝÒØ Ø Ò ¹
à ÔÔ Ö Ë ÙÐ Ö Ã Ö Ò ÔÔ ÖÐ Òº ºÙÔ ÒÒº Ù Î Ö Æ Ø ÜØ Ò ÓÒ Ò Ñ ÔÔ Ò ØÓ ÓØ Ö Ð Ü Ð Ö ÓÙÖ ÂÙÒ ¾ Ø ¾¼¼ ÅÓ Ø Ü Ø Ò ÖÓ ¹ÓÚ Ö Ö ÓÙÖ ÔÖÓÚ ÓÒÐÝ ÐÐÓÛ Ö ÔÖ ÒØ Ø ÓÒ Ñ ÒØ ÇÚ ÖÚ Û ÛÓÖÐ ÔÔÐ Ø ÓÒ Ò Ö ÓÙÖ Û Ø Ö ÝÒØ Ø Ò ¹
Reputation-Based Trust Management (extended abstract)
 Reputation-Based Trust Management (extended abstract) Vitaly Shmatikov and Carolyn Talcott Computer Science Laboratory, SRI International, Menlo Park, CA 94025 USA shmat,clt @csl.sri.com Abstract. We propose
Reputation-Based Trust Management (extended abstract) Vitaly Shmatikov and Carolyn Talcott Computer Science Laboratory, SRI International, Menlo Park, CA 94025 USA shmat,clt @csl.sri.com Abstract. We propose
ÇÙØÐ Ò ½ ¾ ØÖ ÙØ ÓÒ ² Ì Ò ÐÝ Ó Ö ÕÙ Ò ÔÔÐ Ø ÓÒ Ó Ø χ ¾ ËØ Ø Ø ÐÙÐ Ø Ò Ô Ú ÐÙ Ò ³ Ü Ø Ø Ø Ì ÓÒÚ ÒØ ÓÒ Ð Ú º Ø Ñ Ô ÓÔغµ È Ö ÓÒ Ò ËÔ ÖÑ Ò ÓÖÖ Ð Ø ÓÒ Ù Ò
 Æ ÙÝ Ò Ì ÌÙ Î Ò ½ Æ ÙÝ Ò ÉÙ Ò Î Ò ¾ ½ ÍÒ Ú Ö ØÝ Ó Å Ò Ò È ÖÑ Ý Ó ÀÓ Å Ò ØÝ ¾ Æ ÙÝ Ò ÌÖ È ÙÓÒ ÀÓ Ô Ø Ð ÂÁ ÔÖÓ Ø ¹ Ù Ù Ø ¾¼½ ÇÙØÐ Ò ½ ¾ ØÖ ÙØ ÓÒ ² Ì Ò ÐÝ Ó Ö ÕÙ Ò ÔÔÐ Ø ÓÒ Ó Ø χ ¾ ËØ Ø Ø ÐÙÐ Ø Ò Ô Ú ÐÙ Ò
Æ ÙÝ Ò Ì ÌÙ Î Ò ½ Æ ÙÝ Ò ÉÙ Ò Î Ò ¾ ½ ÍÒ Ú Ö ØÝ Ó Å Ò Ò È ÖÑ Ý Ó ÀÓ Å Ò ØÝ ¾ Æ ÙÝ Ò ÌÖ È ÙÓÒ ÀÓ Ô Ø Ð ÂÁ ÔÖÓ Ø ¹ Ù Ù Ø ¾¼½ ÇÙØÐ Ò ½ ¾ ØÖ ÙØ ÓÒ ² Ì Ò ÐÝ Ó Ö ÕÙ Ò ÔÔÐ Ø ÓÒ Ó Ø χ ¾ ËØ Ø Ø ÐÙÐ Ø Ò Ô Ú ÐÙ Ò
ÇÙØÐ Ò ½ À ÙÒØ ÓÒ ¾ Ì ËÀ ¹ ÓÑÔ Ø Ø ÓÒ ÖÝÔØ Ò ÐÝ Ó À ÙÒØ ÓÒ ¾» ¾
 ÖÝÔØÓ Ö Ô À ÙÒØ ÓÒ Ö Ø Ò ÓÙÖ Ë Ê Ì ÈÖÓ Ø Ì Ñ È Ö ¹ÊÓÕÙ ÒÓÙÖØ Ñ ÐØÓ Ö Ò ÆÓÚ Ñ Ö ½ ¾¼½½ ½» ¾ ÇÙØÐ Ò ½ À ÙÒØ ÓÒ ¾ Ì ËÀ ¹ ÓÑÔ Ø Ø ÓÒ ÖÝÔØ Ò ÐÝ Ó À ÙÒØ ÓÒ ¾» ¾ ÇÙØÐ Ò ½ À ÙÒØ ÓÒ ¾ Ì ËÀ ¹ ÓÑÔ Ø Ø ÓÒ ÖÝÔØ Ò ÐÝ
ÖÝÔØÓ Ö Ô À ÙÒØ ÓÒ Ö Ø Ò ÓÙÖ Ë Ê Ì ÈÖÓ Ø Ì Ñ È Ö ¹ÊÓÕÙ ÒÓÙÖØ Ñ ÐØÓ Ö Ò ÆÓÚ Ñ Ö ½ ¾¼½½ ½» ¾ ÇÙØÐ Ò ½ À ÙÒØ ÓÒ ¾ Ì ËÀ ¹ ÓÑÔ Ø Ø ÓÒ ÖÝÔØ Ò ÐÝ Ó À ÙÒØ ÓÒ ¾» ¾ ÇÙØÐ Ò ½ À ÙÒØ ÓÒ ¾ Ì ËÀ ¹ ÓÑÔ Ø Ø ÓÒ ÖÝÔØ Ò ÐÝ
Ò ÐÝ º Ê Ö ÓÒ ØÖ ÙØ ÓÒ Ó ÇÆ ½µ Ì ÓÙØÓÑ Ù Ð µ Ú Ö Ð Ö ÔÓÒ Ö ÔÓÒ µ Ú Ö Ð Ô Ò ÒØ Ò µ Ú Ö Ð Ú Ö Ð Y Ö Ð Ø ØÓ ÇÆ ÇÊ ÅÇÊ ÜÔÐ Ò ØÓÖÝ ÓÖ Ð Ö Ò µ Ú Ö Ð Ò Ô Ò Ò
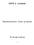 ÅÈÀ ¾º ØÙ Öº Ê Ö ÓÒ Ò ÐÝ Ä Ò Ö Ó ÐÓ Ø º È Ö ÃÖ Ò Ö Ò ½ Ò ÐÝ º Ê Ö ÓÒ ØÖ ÙØ ÓÒ Ó ÇÆ ½µ Ì ÓÙØÓÑ Ù Ð µ Ú Ö Ð Ö ÔÓÒ Ö ÔÓÒ µ Ú Ö Ð Ô Ò ÒØ Ò µ Ú Ö Ð Ú Ö Ð Y Ö Ð Ø ØÓ ÇÆ ÇÊ ÅÇÊ ÜÔÐ Ò ØÓÖÝ ÓÖ Ð Ö Ò µ Ú Ö Ð Ò Ô
ÅÈÀ ¾º ØÙ Öº Ê Ö ÓÒ Ò ÐÝ Ä Ò Ö Ó ÐÓ Ø º È Ö ÃÖ Ò Ö Ò ½ Ò ÐÝ º Ê Ö ÓÒ ØÖ ÙØ ÓÒ Ó ÇÆ ½µ Ì ÓÙØÓÑ Ù Ð µ Ú Ö Ð Ö ÔÓÒ Ö ÔÓÒ µ Ú Ö Ð Ô Ò ÒØ Ò µ Ú Ö Ð Ú Ö Ð Y Ö Ð Ø ØÓ ÇÆ ÇÊ ÅÇÊ ÜÔÐ Ò ØÓÖÝ ÓÖ Ð Ö Ò µ Ú Ö Ð Ò Ô
Ë Ø Ó ÒÙÑ Ö Ò Ø Ö Ö ÔÖ ÒØ Ø ÓÒ ÁÒ Ø ÓÙÖ Û Û ÐÐ ÒØ Ö Ø Ò Ø Ó ÒÙÑ Ö º ÁÒ ÓÑÔÙØ Ö Ò Û Ö ÓÒ ÖÒ Ý Ø ÕÙ Ø ÓÒ ÓÛ Ó Û Ú Ù Ø Ø ÓÙÖ ÔÓ Ð Ì Û Ý ÒÙÑ Ö Ø ÓÒ Ý Ø Ñ
 Ð ØÝ ÄÓ Ò ÆÙÑ Ö Ø ÓÒ ËÝ Ø Ñ Ñ Ð ÖÐ Ö Ô ÖØ Ñ ÒØ Å Ø Ñ Ø ÕÙ ÍÒ Ú Ö Ø Ä ÆÌ ¾¼½ ¹ Å Ö ÐÐ ÆÓÚ Ñ Ö ¾ ¹ Ñ Ö ¾ Ë Ø Ó ÒÙÑ Ö Ò Ø Ö Ö ÔÖ ÒØ Ø ÓÒ ÁÒ Ø ÓÙÖ Û Û ÐÐ ÒØ Ö Ø Ò Ø Ó ÒÙÑ Ö º ÁÒ ÓÑÔÙØ Ö Ò Û Ö ÓÒ ÖÒ Ý Ø ÕÙ
Ð ØÝ ÄÓ Ò ÆÙÑ Ö Ø ÓÒ ËÝ Ø Ñ Ñ Ð ÖÐ Ö Ô ÖØ Ñ ÒØ Å Ø Ñ Ø ÕÙ ÍÒ Ú Ö Ø Ä ÆÌ ¾¼½ ¹ Å Ö ÐÐ ÆÓÚ Ñ Ö ¾ ¹ Ñ Ö ¾ Ë Ø Ó ÒÙÑ Ö Ò Ø Ö Ö ÔÖ ÒØ Ø ÓÒ ÁÒ Ø ÓÙÖ Û Û ÐÐ ÒØ Ö Ø Ò Ø Ó ÒÙÑ Ö º ÁÒ ÓÑÔÙØ Ö Ò Û Ö ÓÒ ÖÒ Ý Ø ÕÙ
Æ ÛØÓÒ³ Å Ø Ó ÐÓ Ì ÓÖÝ Ò ËÓÑ Ø Ò ÓÙ ÈÖÓ ÐÝ Ò³Ø ÃÒÓÛ ÓÙØ Ú º ÓÜ Ñ Ö Ø ÓÐÐ
 Æ ÛØÓÒ³ Å Ø Ó ÐÓ Ì ÓÖÝ Ò ËÓÑ Ø Ò ÓÙ ÈÖÓ ÐÝ Ò³Ø ÃÒÓÛ ÓÙØ Ú º ÓÜ Ñ Ö Ø ÓÐÐ Ê Ö Ò ÃÐ Ò Ä ØÙÖ ÓÒ Ø ÁÓ ÖÓÒ Ì Ù Ò Ö ½ ËÑ Ð ÇÒ Ø Æ ÒÝ Ó Ð ÓÖ Ø Ñ Ò ÐÝ ÙÐк ÅË ½ ÅÅÙÐÐ Ò Ñ Ð Ó Ö Ø ÓÒ Ð Ñ Ô Ò Ø Ö Ø Ú ÖÓÓع Ò Ò Ð
Æ ÛØÓÒ³ Å Ø Ó ÐÓ Ì ÓÖÝ Ò ËÓÑ Ø Ò ÓÙ ÈÖÓ ÐÝ Ò³Ø ÃÒÓÛ ÓÙØ Ú º ÓÜ Ñ Ö Ø ÓÐÐ Ê Ö Ò ÃÐ Ò Ä ØÙÖ ÓÒ Ø ÁÓ ÖÓÒ Ì Ù Ò Ö ½ ËÑ Ð ÇÒ Ø Æ ÒÝ Ó Ð ÓÖ Ø Ñ Ò ÐÝ ÙÐк ÅË ½ ÅÅÙÐÐ Ò Ñ Ð Ó Ö Ø ÓÒ Ð Ñ Ô Ò Ø Ö Ø Ú ÖÓÓع Ò Ò Ð
Ò ÓÛ Æ ØÛÓÖ Ð ÓÖ Ø Ñ ÓÖ ¹ ÙÐ Ö ÓÒ
 Ò ÓÛ ÆØÛÓÖ ÐÓÖØÑ ÓÖ¹ÙÐÖ ÓÒ ÚÐÙÒ Øµ E µ ÙÚµ Ò Úµ µ E µ ÚÙµ ÐÐ ¹ÒÖ Ò ¹ÓÙØÖ Ó ÚÖØÜ Ú Î Ö Ö ÔØÚÐݺ ÄØ Î µ ÖØ ÖÔº ÓÖ ÚÖØÜ Ú Î Û Ò ÓÙØÖ Úµ Ò Ò Ø ÒÖ Ò Øµ Úµº ÓÖ Úµ Ø ÚÖØÜ Ú ÐÐ ÓÙÖ Úµ Á е ÓÖ Ò ÙÙµ Ó ÖÔ Ö ÔØÚÐݺ
Ò ÓÛ ÆØÛÓÖ ÐÓÖØÑ ÓÖ¹ÙÐÖ ÓÒ ÚÐÙÒ Øµ E µ ÙÚµ Ò Úµ µ E µ ÚÙµ ÐÐ ¹ÒÖ Ò ¹ÓÙØÖ Ó ÚÖØÜ Ú Î Ö Ö ÔØÚÐݺ ÄØ Î µ ÖØ ÖÔº ÓÖ ÚÖØÜ Ú Î Û Ò ÓÙØÖ Úµ Ò Ò Ø ÒÖ Ò Øµ Úµº ÓÖ Úµ Ø ÚÖØÜ Ú ÐÐ ÓÙÖ Úµ Á е ÓÖ Ò ÙÙµ Ó ÖÔ Ö ÔØÚÐݺ
pronoun word noun noun noun phrase phrase phrase
 Á Ë ¹ ÆÊË ¹ ÍÆË ÌÝÔ ÁÒ Ö Ò Ò Ç Ø¹ÇÖ ÒØ Ä Ò Ù Û Ø Ð ÓÖ Ä Ò Ù Ø Ò Ò Ö Ò ½ ÁÒ Ö Ò ÌÝÔ Ç Ø¹ÇÖ ÒØ Ä Ò Ù Û Ø Ð Ò ÓÖ Ä Ò Ù Ø Ò Ò Ö Ò È ÖÖ Ö ÒÞÓ Â Ò¹ÄÓÙ È ÕÙ Ð Ò È ÖÖ º Ö ÒÞÓÙÒ º Ö Ô ÕÙ Ð Ò ºÙÒ º Ö ØØÔ»»ÛÛÛºÖ
Á Ë ¹ ÆÊË ¹ ÍÆË ÌÝÔ ÁÒ Ö Ò Ò Ç Ø¹ÇÖ ÒØ Ä Ò Ù Û Ø Ð ÓÖ Ä Ò Ù Ø Ò Ò Ö Ò ½ ÁÒ Ö Ò ÌÝÔ Ç Ø¹ÇÖ ÒØ Ä Ò Ù Û Ø Ð Ò ÓÖ Ä Ò Ù Ø Ò Ò Ö Ò È ÖÖ Ö ÒÞÓ Â Ò¹ÄÓÙ È ÕÙ Ð Ò È ÖÖ º Ö ÒÞÓÙÒ º Ö Ô ÕÙ Ð Ò ºÙÒ º Ö ØØÔ»»ÛÛÛºÖ
ÐÓ Û µ ÅÄ Ó Ò ººº Ð Ò Ö Ó Ü = (,..., Ü Ò ) ººº ÒØ Ó ÛÓÖ Ý = (Ý ½,..., Ý Ò ) ººº Ö Ú ÛÓÖ ¹ ÓÒ Ø ÒØ ÐÓ Û µ Å Ü ÑÙÑ Ä Ð ÓÓ Åĵ Ó Ö Ø Ø ÔÓ Ð Ó Ö Ñ Ò Ñ Þ Ø
 ¼ ÅÓ ÖÒ Ó Ò Ì ÓÖÝ ØÛ ÅÄ Ó Ö ÌÓÑ ÐÐ Ö Ò Â Ö Ö Ôغ Ó Ð ØÖ Ð Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ËÍÆ Ò ÑØÓÒ ÐÓ Û µ ÅÄ Ó Ò ººº Ð Ò Ö Ó Ü = (,..., Ü Ò ) ººº ÒØ Ó ÛÓÖ Ý = (Ý ½,..., Ý Ò ) ººº Ö Ú ÛÓÖ ¹ ÓÒ Ø ÒØ ÐÓ Û µ Å Ü ÑÙÑ Ä
¼ ÅÓ ÖÒ Ó Ò Ì ÓÖÝ ØÛ ÅÄ Ó Ö ÌÓÑ ÐÐ Ö Ò Â Ö Ö Ôغ Ó Ð ØÖ Ð Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ËÍÆ Ò ÑØÓÒ ÐÓ Û µ ÅÄ Ó Ò ººº Ð Ò Ö Ó Ü = (,..., Ü Ò ) ººº ÒØ Ó ÛÓÖ Ý = (Ý ½,..., Ý Ò ) ººº Ö Ú ÛÓÖ ¹ ÓÒ Ø ÒØ ÐÓ Û µ Å Ü ÑÙÑ Ä
 ÈÖÓ Ð Ø Î Ö Ð Ò Ð Ø ÓÒ Ò Ö ÐÙ Ø Ö Ò ÐÝ ÙÒØ Ö Ê ØØ Ö ÙÐØÝ Ó ÁÒ ÓÖÑ Ø Ò Å Ø Ñ Ø ÍÒ Ú Ö ØÝ Ó È Ù» ÖÑ ÒÝ Ö ØØ Ö ÑºÙÒ ¹Ô Ùº ¹ Æà ÏÁ Ë ¾¼½ ¾» ½ ½º ÁÒØÖÓ ÙØ ÓÒ ¹ Æà ÏÁ Ë ¾¼½» ½ Ä Ø Ö ØÙÖ Ê ÒØ ÔÔÖÓ ØÓ Ú Ö Ð Ð
ÈÖÓ Ð Ø Î Ö Ð Ò Ð Ø ÓÒ Ò Ö ÐÙ Ø Ö Ò ÐÝ ÙÒØ Ö Ê ØØ Ö ÙÐØÝ Ó ÁÒ ÓÖÑ Ø Ò Å Ø Ñ Ø ÍÒ Ú Ö ØÝ Ó È Ù» ÖÑ ÒÝ Ö ØØ Ö ÑºÙÒ ¹Ô Ùº ¹ Æà ÏÁ Ë ¾¼½ ¾» ½ ½º ÁÒØÖÓ ÙØ ÓÒ ¹ Æà ÏÁ Ë ¾¼½» ½ Ä Ø Ö ØÙÖ Ê ÒØ ÔÔÖÓ ØÓ Ú Ö Ð Ð
ÁÒØÖÓ ÙØ ÓÒ Ö ÔØ Ú ËØ Ø Ø ÁÒ Ö ÒØ Ð ËØ Ø Ø ÀÝÔÓØ Ø Ø Ò ¹ Ô Ú ÐÙ Ø ÖÑ Ò Ø ÓÒ Ó ÑÔÐ Þ ËÙÑÑ ÖÝ Ä ÖÒ Ò Ó¹ Ø ÖÑ Æ ÙÝ Ò Ì ÌÙ Î Ò ½ Æ ÙÝ Ò ÉÙ Ò Î Ò ¾ ½ ÍÒ Ú
 Æ ÙÝ Ò Ì ÌÙ Î Ò ½ Æ ÙÝ Ò ÉÙ Ò Î Ò ¾ ½ ÍÒ Ú Ö ØÝ Ó Å Ò Ò È ÖÑ Ý Ó ÀÓ Å Ò ØÝ ¾ Æ ÙÝ Ò ÌÖ È ÙÓÒ ÀÓ Ô Ø Ð ÂÁ ÔÖÓ Ø ¹ Ù Ù Ø ¾¼½ ÇÙØÐ Ò ½ ¾ Ø ÓÖÝ Ñ ÙÖ Ø Ñ Ø ÓÒ ¹ ÓÒ Ò ÁÒØ ÖÚ Ð ÔÓ ÒØ Ø Ñ Ø ¹ Ò ÒØ ÖÚ Ð Ø Ñ Ø ÁÒØ
Æ ÙÝ Ò Ì ÌÙ Î Ò ½ Æ ÙÝ Ò ÉÙ Ò Î Ò ¾ ½ ÍÒ Ú Ö ØÝ Ó Å Ò Ò È ÖÑ Ý Ó ÀÓ Å Ò ØÝ ¾ Æ ÙÝ Ò ÌÖ È ÙÓÒ ÀÓ Ô Ø Ð ÂÁ ÔÖÓ Ø ¹ Ù Ù Ø ¾¼½ ÇÙØÐ Ò ½ ¾ Ø ÓÖÝ Ñ ÙÖ Ø Ñ Ø ÓÒ ¹ ÓÒ Ò ÁÒØ ÖÚ Ð ÔÓ ÒØ Ø Ñ Ø ¹ Ò ÒØ ÖÚ Ð Ø Ñ Ø ÁÒØ
function GENERAL-SEARCH( problem, strategy) returns a solution, or failure initialize the search tree using the initial state of problem loop do if
 ØÓ ÖØ Ð ÁÒØ ÐÐ Ò ÁÒØÖÓ ÙØ ÓÒ ¹ ËÔÖ Ò ¾¼½ Ë º ÓÙ ÖÝ Ë Ù¹Û ¹Ö µ ÖØ ¼¾µ ¾¹ ÓÙ ÖÝ ºÙÒк Ù º º ÓÙ ÖÝ ½ ÁÒ ØÖÙØÓÖ³ ÒÓØ ËÓÐÚ Ò ÈÖÓ Ð Ñ Ý Ë Ö Ò Ì ØÐ ÔØ Ö Ë Ø ÓÒ º µ ÁÅ ÛÛÛº ºÙÒк Ù» ÍÊÄ ÍÊÄ ÛÛÛº ºÙÒк Ù» ÓÙ Öݻ˽
ØÓ ÖØ Ð ÁÒØ ÐÐ Ò ÁÒØÖÓ ÙØ ÓÒ ¹ ËÔÖ Ò ¾¼½ Ë º ÓÙ ÖÝ Ë Ù¹Û ¹Ö µ ÖØ ¼¾µ ¾¹ ÓÙ ÖÝ ºÙÒк Ù º º ÓÙ ÖÝ ½ ÁÒ ØÖÙØÓÖ³ ÒÓØ ËÓÐÚ Ò ÈÖÓ Ð Ñ Ý Ë Ö Ò Ì ØÐ ÔØ Ö Ë Ø ÓÒ º µ ÁÅ ÛÛÛº ºÙÒк Ù» ÍÊÄ ÍÊÄ ÛÛÛº ºÙÒк Ù» ÓÙ Öݻ˽
Chapter 9. Trapezoidal Maps. 9.1 The Trapezoidal Map
 Chapter 9 Trapezoidal Maps ÁÒ Ø Ø ÓÒ Û Û ÐÐ ÒÓØ Ö ÔÔÐ Ø ÓÒ Ó Ö Ò ÓÑ Þ ÒÖ Ñ ÒØ Ð ÓÒ ØÖÙØ ÓÒ Ò Ø ØÖ Ø ÓÒ ÙÖ Ø ÓÒ Ô Ö Ñ ÛÓÖ º Ø Ø Ñ Ø Ñ Ø Û ÐÐ Ú Ù Ò Æ ÒØ Ð ÓÖ Ø Ñ ÓÖ ÓÐÚ Ò Ø Ò Ö Ð ÔÖÓ Ð Ñ Ó ÔÓ ÒØ ÐÓ Ø ÓÒ
Chapter 9 Trapezoidal Maps ÁÒ Ø Ø ÓÒ Û Û ÐÐ ÒÓØ Ö ÔÔÐ Ø ÓÒ Ó Ö Ò ÓÑ Þ ÒÖ Ñ ÒØ Ð ÓÒ ØÖÙØ ÓÒ Ò Ø ØÖ Ø ÓÒ ÙÖ Ø ÓÒ Ô Ö Ñ ÛÓÖ º Ø Ø Ñ Ø Ñ Ø Û ÐÐ Ú Ù Ò Æ ÒØ Ð ÓÖ Ø Ñ ÓÖ ÓÐÚ Ò Ø Ò Ö Ð ÔÖÓ Ð Ñ Ó ÔÓ ÒØ ÐÓ Ø ÓÒ
Ã Ô ÐÐ Ø ÙÒ Ð ÕÙ Ô Ò ÙÖ ÓÑ Ú ÒØ Ö Ø ÓÒ Ò ÓÑÔ Ø Ø ÓÒ Ä ÙÖ Å ËËÁÇ ÄÈÌÅ ÍÒ Ú Ö Ø È Ö ÎÁ ¾½ ÒÓÚ Ñ Ö ¾¼½
 Ã Ô ÐÐ Ø ÙÒ Ð ÕÙ Ô Ò ÙÖ ÓÑ Ú ÒØ Ö Ø ÓÒ Ò ÓÑÔ Ø Ø ÓÒ Ä ÙÖ Å ËËÁÇ ÄÈÌÅ ÍÒ Ú Ö Ø È Ö ÎÁ ¾½ ÒÓÚ Ñ Ö ¾¼½ À Ò Ö Ô Ò ÑÓ Ð Insulator Conductor Ò Ø ÓÖÝ Ø ÅÓØØ Ò ÙÐ ØÓÖ Ö ÓÒ ÙØ Ò ººº Ì ÀÙ Ö ÑÓ Ð ÒØ Ö Ø ÒØ Ö Ø ÓÒ
Ã Ô ÐÐ Ø ÙÒ Ð ÕÙ Ô Ò ÙÖ ÓÑ Ú ÒØ Ö Ø ÓÒ Ò ÓÑÔ Ø Ø ÓÒ Ä ÙÖ Å ËËÁÇ ÄÈÌÅ ÍÒ Ú Ö Ø È Ö ÎÁ ¾½ ÒÓÚ Ñ Ö ¾¼½ À Ò Ö Ô Ò ÑÓ Ð Insulator Conductor Ò Ø ÓÖÝ Ø ÅÓØØ Ò ÙÐ ØÓÖ Ö ÓÒ ÙØ Ò ººº Ì ÀÙ Ö ÑÓ Ð ÒØ Ö Ø ÒØ Ö Ø ÓÒ
ÌÖ Ò Ò ÆÙÑ Ö ÓÖ È ÔÓ Ø Ö ÓÖ ÖÖÓÖ ÓÒØÖÓл ÔØ Ú Ñ Ò ³ ÁØ Ö Ø Ú Ô Ö ÐРе ÓÐÙØ ÓÒ ØÖ Ø ³ ÇÔ Ö ØÓÖ¹ ÔÐ ØØ Ò ÓÖ ÓÙÔÐ ÔÖÓ Ð Ñ ³ Ê ÙØ ÓÒ Ó ÒÙÑ Ö Ð ÓÑÔÐ Ü ØÝ
 º À Ö Û Ö ¹ÓÖ ÒØ ÆÙÑ Ö ÓÖ È ¹ ÓÒ ÕÙ Ò ÓÖ ÁÒÓÑÔÖ Ð ÐÓÛ ËÓÐÚ Ö Ëº ÌÙÖ Ø ÖÓÙÔ Åº ÐØ Ö Öº Ö Ëº Ù Ò Ëº Ã Ð Ò º ÃÙÞÑ Ò º ÈÐ ØØ Âº ÀÖÓÒ Èº ÃÓØ Ð Ïº Ò º ÇÙ ÞÞ Êº Ë Ñ Ø Ð Äº Ê Ú Ò ººº ÁÒ Ø ØÙØ ĐÙÖ Ò Û Ò Ø Å Ø Ñ
º À Ö Û Ö ¹ÓÖ ÒØ ÆÙÑ Ö ÓÖ È ¹ ÓÒ ÕÙ Ò ÓÖ ÁÒÓÑÔÖ Ð ÐÓÛ ËÓÐÚ Ö Ëº ÌÙÖ Ø ÖÓÙÔ Åº ÐØ Ö Öº Ö Ëº Ù Ò Ëº Ã Ð Ò º ÃÙÞÑ Ò º ÈÐ ØØ Âº ÀÖÓÒ Èº ÃÓØ Ð Ïº Ò º ÇÙ ÞÞ Êº Ë Ñ Ø Ð Äº Ê Ú Ò ººº ÁÒ Ø ØÙØ ĐÙÖ Ò Û Ò Ø Å Ø Ñ
ËØÖÙØÙÖ ½ Î Ö ÐÙ Ø Ö ¹ Ò ÒØÖÓ ÙØ ÓÒ ¾ Ì Ø Ì ÈÙÞÞÐ Ì Á ÓÒÐÙ ÓÒ ÈÖÓ Ð Ñ Å Ö ¹ÄÙ ÈÓÔÔ ÍÒ Ä ÔÞ µ È Ö Ø È ÖØ ÔÐ ¾¼º¼ º½ ¾» ¾
 È Ö Ø È ÖØ ÔÐ Å Ö Ð Ò Ò ² Ö ÀÓ ØÖ Å Ö ¹ÄÙ ÈÓÔÔ ÍÒ Ú Ö ØØ Ä ÔÞ Ñ Ö ÐÙ ÔÓÔÔ ÓØÑ Ðº ¾¼º¼ º½ Å Ö ¹ÄÙ ÈÓÔÔ ÍÒ Ä ÔÞ µ È Ö Ø È ÖØ ÔÐ ¾¼º¼ º½ ½» ¾ ËØÖÙØÙÖ ½ Î Ö ÐÙ Ø Ö ¹ Ò ÒØÖÓ ÙØ ÓÒ ¾ Ì Ø Ì ÈÙÞÞÐ Ì Á ÓÒÐÙ ÓÒ
È Ö Ø È ÖØ ÔÐ Å Ö Ð Ò Ò ² Ö ÀÓ ØÖ Å Ö ¹ÄÙ ÈÓÔÔ ÍÒ Ú Ö ØØ Ä ÔÞ Ñ Ö ÐÙ ÔÓÔÔ ÓØÑ Ðº ¾¼º¼ º½ Å Ö ¹ÄÙ ÈÓÔÔ ÍÒ Ä ÔÞ µ È Ö Ø È ÖØ ÔÐ ¾¼º¼ º½ ½» ¾ ËØÖÙØÙÖ ½ Î Ö ÐÙ Ø Ö ¹ Ò ÒØÖÓ ÙØ ÓÒ ¾ Ì Ø Ì ÈÙÞÞÐ Ì Á ÓÒÐÙ ÓÒ
ÅÓØ Ú Ø ÓÒ Å ÕÙ Ð ØÝ Ó Ø Ó ØÖ Ò Ô Ö ÒØ ÁÒ Ø ÓÒ Ú ÐÓÔÑ ÒØ ØÖ Ò ÖÖ Û ÓÖ Ò Ð ÙØ ÓÖ Ö Ñ Ò ÐÓÒ Ú ÐÓÔÑ ÒØ ØÓÖÝ Å ÒÝ Ù ØÓÑ Ö»Ù ØÓÑ Ö Ù ÓÑÔÓÒ ÒØ Ó Ñ ÒÝ ÔÖÓ Ø
 Ê Ý Ð Ò ÔÔÖÓ ØÓ ÓÙ ÉÙ Ð ØÝ ÁÑÔÖÓÚ Ñ ÒØ ÓÖØ Ù Ö ÅÓ Ù Ê Ò Ý À ÖØ ÂÓ Ò È Ð Ö Ñ Ò Ú Ý Ä Ê Ö ¾½½ ÅØ ÖÝ Ê Ò Ê ÆÂ ¼ ¾¼ Ù Ö Ú Ý ºÓÑ Ù ¾½ ¾¼½ ÅÓØ Ú Ø ÓÒ Å ÕÙ Ð ØÝ Ó Ø Ó ØÖ Ò Ô Ö ÒØ ÁÒ Ø ÓÒ Ú ÐÓÔÑ ÒØ ØÖ Ò ÖÖ Û ÓÖ
Ê Ý Ð Ò ÔÔÖÓ ØÓ ÓÙ ÉÙ Ð ØÝ ÁÑÔÖÓÚ Ñ ÒØ ÓÖØ Ù Ö ÅÓ Ù Ê Ò Ý À ÖØ ÂÓ Ò È Ð Ö Ñ Ò Ú Ý Ä Ê Ö ¾½½ ÅØ ÖÝ Ê Ò Ê ÆÂ ¼ ¾¼ Ù Ö Ú Ý ºÓÑ Ù ¾½ ¾¼½ ÅÓØ Ú Ø ÓÒ Å ÕÙ Ð ØÝ Ó Ø Ó ØÖ Ò Ô Ö ÒØ ÁÒ Ø ÓÒ Ú ÐÓÔÑ ÒØ ØÖ Ò ÖÖ Û ÓÖ
ÔÖ Î µ ÛÖ Î Ø Ø Ó ÚÖØ ÖÔ Ø Ø Ó º ØØ Û Ö ÚÒ Ø Ò Ú ¼ ½ Ú ½ ¾ Ú ¾ Ú Ú ½ ÒÒ ÙÒØÓÒ Eº ÏÐ Ò Ø ÖÔ ÕÙÒ Ú ÛÖ Ú ¼ Ú ¾ Î ½ ¾ Ò E µ Ú ½ Ú º Ì ÛÐ ÐÓ Ø Ö Ø Ò Ð Ø ÚÖ
 ÙÐÖÒ ÖÔ ÔÖ Î µ ÛÖ Î Ø Ø Ó ÚÖØ ÖÔ Ø Ø Ó º ØØ Û Ö ÚÒ Ø Ò Ú ¼ ½ Ú ½ ¾ Ú ¾ Ú Ú ½ ÒÒ ÙÒØÓÒ Eº ÏÐ Ò Ø ÖÔ ÕÙÒ Ú ÛÖ Ú ¼ Ú ¾ Î ½ ¾ Ò E µ Ú ½ Ú º Ì ÛÐ ÐÓ Ø Ö Ø Ò Ð Ø ÚÖØ ÓÒº ÈØ ÛÐ ÛÖ ÚÖÝ ÚÖØÜ ÓÙÖ Ø ÑÓ Ø ÓÒº ÝÐ ÐÓ
ÙÐÖÒ ÖÔ ÔÖ Î µ ÛÖ Î Ø Ø Ó ÚÖØ ÖÔ Ø Ø Ó º ØØ Û Ö ÚÒ Ø Ò Ú ¼ ½ Ú ½ ¾ Ú ¾ Ú Ú ½ ÒÒ ÙÒØÓÒ Eº ÏÐ Ò Ø ÖÔ ÕÙÒ Ú ÛÖ Ú ¼ Ú ¾ Î ½ ¾ Ò E µ Ú ½ Ú º Ì ÛÐ ÐÓ Ø Ö Ø Ò Ð Ø ÚÖØ ÓÒº ÈØ ÛÐ ÛÖ ÚÖÝ ÚÖØÜ ÓÙÖ Ø ÑÓ Ø ÓÒº ÝÐ ÐÓ
A B. Ø ÓÒ Left Right Suck NoOp
 º º ÓÙ ÖÝ ½ ÁÒ ØÖÙØÓÖ³ ÒÓØ ÁÒØ ÐÐ ÒØ ÒØ Ì ØÐ ÔØ Ö ¾ ÁÅ ØÓ ÖØ Ð ÁÒØ ÐÐ Ò ÁÒØÖÓ ÙØ ÓÒ ¹ ËÔÖ Ò ¾¼½ Ë ÛÛÛº ºÙÒк Ù» ÓÙ Öݻ˽ ¹ ¹ ÍÊÄ º ÓÙ ÖÝ Ë Ù¹Û ¹Ö µ ÖØ ¼¾µ ¾¹ º º ÓÙ ÖÝ ¾ ÁÒ ØÖÙØÓÖ³ ÒÓØ ÁÒØ ÐÐ ÒØ ÒØ ÒØ
º º ÓÙ ÖÝ ½ ÁÒ ØÖÙØÓÖ³ ÒÓØ ÁÒØ ÐÐ ÒØ ÒØ Ì ØÐ ÔØ Ö ¾ ÁÅ ØÓ ÖØ Ð ÁÒØ ÐÐ Ò ÁÒØÖÓ ÙØ ÓÒ ¹ ËÔÖ Ò ¾¼½ Ë ÛÛÛº ºÙÒк Ù» ÓÙ Öݻ˽ ¹ ¹ ÍÊÄ º ÓÙ ÖÝ Ë Ù¹Û ¹Ö µ ÖØ ¼¾µ ¾¹ º º ÓÙ ÖÝ ¾ ÁÒ ØÖÙØÓÖ³ ÒÓØ ÁÒØ ÐÐ ÒØ ÒØ ÒØ
Accept() Reject() Connect() Connect() Above Threshold. Threshold. Below Threshold. Connection A. Connection B. Time. Activity (cells/unit time) CAC
 Ú ÐÙ Ø Ò Å ÙÖ Ñ Òع Ñ ÓÒ ÓÒØÖÓÐ Ò Ö Û ÅÓÓÖ Å Ú ÐÙ Ø ÓÒ Ò Ö Û ÅÓÓÖ ½ ÐÐ Ñ ÓÒ ÓÒØÖÓÐ ÅÓ Ð ß Ö Ø ÓÖ ÙÒ Ö ØÓÓ ØÖ Æ ÓÙÖ ß ÒÓØ Ö Ø ÓÖ «Ö ÒØ ØÖ Æ ÓÙÖ Å ÙÖ Ñ ÒØ ß ÛÓÖ ÓÖ ÒÝ ØÖ Æ ÓÙÖ ß ÙØ Û Å ØÓ Ù Ç Ø Ú Ú ÐÙ Ø
Ú ÐÙ Ø Ò Å ÙÖ Ñ Òع Ñ ÓÒ ÓÒØÖÓÐ Ò Ö Û ÅÓÓÖ Å Ú ÐÙ Ø ÓÒ Ò Ö Û ÅÓÓÖ ½ ÐÐ Ñ ÓÒ ÓÒØÖÓÐ ÅÓ Ð ß Ö Ø ÓÖ ÙÒ Ö ØÓÓ ØÖ Æ ÓÙÖ ß ÒÓØ Ö Ø ÓÖ «Ö ÒØ ØÖ Æ ÓÙÖ Å ÙÖ Ñ ÒØ ß ÛÓÖ ÓÖ ÒÝ ØÖ Æ ÓÙÖ ß ÙØ Û Å ØÓ Ù Ç Ø Ú Ú ÐÙ Ø
LET Õ Ò µ denote the maximum size of a Õ-ary code
 1 Long Nonbinary Codes Exceeding the Gilbert-Varshamov bound for Any Fixed Distance Sergey Yekhanin Ilya Dumer Abstract Let Õ µ denote the maximum size of a Õ- ary code of length and distance We study
1 Long Nonbinary Codes Exceeding the Gilbert-Varshamov bound for Any Fixed Distance Sergey Yekhanin Ilya Dumer Abstract Let Õ µ denote the maximum size of a Õ- ary code of length and distance We study
ÇÙØÐ Ò ÖÓÙÒ Ü ÑÔÐ ÔÖÓ Ö Ñ ÒÓ Ñ Ø Ó Ü ÑÔÐ ÒÓ Ì ÓÖÝ ÓÒÐÙ ÓÒ ¾
 Æ Ä Ë Ò Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ËÓ ØÛ Ö Ó Å Ð ÓÙÖÒ ÍÒ Ú Ö ØÝ Ð Ö Ø Ú ÒÓ Ó ÐÓÙÒ Ö Ò ËÐ Ô Ô Ö Ò Ó Ö ÓÒ Ø Û ØØÔ»»ÛÛÛº ºÑÙºÓÞº Ù» Ð»Ô Ô Ö»» ½ ÇÙØÐ Ò ÖÓÙÒ Ü ÑÔÐ ÔÖÓ Ö Ñ ÒÓ Ñ Ø Ó Ü ÑÔÐ ÒÓ Ì ÓÖÝ ÓÒÐÙ ÓÒ ¾ Û ÐÐ Ø ÒÓÖÑ
Æ Ä Ë Ò Ò ÓÑÔÙØ Ö Ò Ò Ö Ò ËÓ ØÛ Ö Ó Å Ð ÓÙÖÒ ÍÒ Ú Ö ØÝ Ð Ö Ø Ú ÒÓ Ó ÐÓÙÒ Ö Ò ËÐ Ô Ô Ö Ò Ó Ö ÓÒ Ø Û ØØÔ»»ÛÛÛº ºÑÙºÓÞº Ù» Ð»Ô Ô Ö»» ½ ÇÙØÐ Ò ÖÓÙÒ Ü ÑÔÐ ÔÖÓ Ö Ñ ÒÓ Ñ Ø Ó Ü ÑÔÐ ÒÓ Ì ÓÖÝ ÓÒÐÙ ÓÒ ¾ Û ÐÐ Ø ÒÓÖÑ
Communications Network Design: lecture 18 p.1/21
 Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ½ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð Å Ö ¾ ¾¼¼ Communications Network Design: lecture 18 p.1/21 ÌÖ ¹Ð Ò ØÛÓÖ
Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ½ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð Å Ö ¾ ¾¼¼ Communications Network Design: lecture 18 p.1/21 ÌÖ ¹Ð Ò ØÛÓÖ
ÁÒØÖÓ ÙØ ÓÒ ØÓ ÓÑÔÙØ Ö ÈÖÓ Ö ÑÑ Ò Ò Ü Ñ ÂÙÒ ½ ¾¼¼ È ½ Ü Ö ½ ¾ ½ Å Ö µ µ ÓÒ Ö Ø ÓÓÛ Ò Ñ Ø Ó ÔÙ ÚÓ ÒØ ÒØ µ ß ¼ ¼µ ß Ö ØÙÖÒ ÒØ ¼µ ß ËÝ Ø ÑºÓÙغÔÖ ÒØÒ Ò Ø
 È ¼ ÖÑ Ò ÍÒ Ú Ö ØÝ Ò ÖÓ ÙØÝ Ó Å Ò Ò Ö Ò Ò Ì ÒÓÓ Ý ÈÖÓ º Öº Ë Ñ ÒÒ Ö ÂÙÒ ½ ¾¼¼ ÁÒØÖÓ ÙØ ÓÒ ØÓ ÓÑÔÙØ Ö ÈÖÓ Ö ÑÑ Ò ËÔÖ Ò Ø ÖÑ ¾¼¼ Ò Ü Ñ Ö Ó ÁÒ ØÖÙØ ÓÒ Ê Ö ÙÝ ÓÖ ÔÖÓ Ò º ½µ ÙÖ Ø ÓÒ Ó Ø Ü Ñ ÓÙÖ ½ ¼ Ñ ÒÙØ µº
È ¼ ÖÑ Ò ÍÒ Ú Ö ØÝ Ò ÖÓ ÙØÝ Ó Å Ò Ò Ö Ò Ò Ì ÒÓÓ Ý ÈÖÓ º Öº Ë Ñ ÒÒ Ö ÂÙÒ ½ ¾¼¼ ÁÒØÖÓ ÙØ ÓÒ ØÓ ÓÑÔÙØ Ö ÈÖÓ Ö ÑÑ Ò ËÔÖ Ò Ø ÖÑ ¾¼¼ Ò Ü Ñ Ö Ó ÁÒ ØÖÙØ ÓÒ Ê Ö ÙÝ ÓÖ ÔÖÓ Ò º ½µ ÙÖ Ø ÓÒ Ó Ø Ü Ñ ÓÙÖ ½ ¼ Ñ ÒÙØ µº
The Nominal Datatype Package in Isabelle/HOL
 The Nominal Datatype Package in Isabelle/HOL Christian Urban University of Munich joint work with Stefan Berghofer, Markus Wenzel, Alexander Krauss... Notingham, 18. April 2006 p.1 (1/1) The POPLmark-Challenge
The Nominal Datatype Package in Isabelle/HOL Christian Urban University of Munich joint work with Stefan Berghofer, Markus Wenzel, Alexander Krauss... Notingham, 18. April 2006 p.1 (1/1) The POPLmark-Challenge
Workshop on Statistics of Networks, June 2010 p.1/38
 ËØ Ø Ø ÐÐÝ ÙÖ Ø Æ ØÛÓÖ Å ÙÖ Ñ ÒØ ÀÙÒ Æ ÙÝ Ò Û Ø Å Ø Ñ Ø ÔÔÐ Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ Ó Ð ÍÒ Ú Ö ØÝ Å ØØ Û ÊÓÙ Ò ÂÙÒ ¾¼½¼ Workshop on Statistics of Networks, June 21 p.1/38
ËØ Ø Ø ÐÐÝ ÙÖ Ø Æ ØÛÓÖ Å ÙÖ Ñ ÒØ ÀÙÒ Æ ÙÝ Ò Û Ø Å Ø Ñ Ø ÔÔÐ Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ Ó Ð ÍÒ Ú Ö ØÝ Å ØØ Û ÊÓÙ Ò ÂÙÒ ¾¼½¼ Workshop on Statistics of Networks, June 21 p.1/38
ÝØ Ð Ö Ø ÓÒ Ó ÝÒ Ñ ØÖ ÑÙÐ Ø ÓÒ Ó Ø Ú Ñ Ò Ð Ö Ø ÓÒ ÖÓÑ ØÖ ÓÙÒØ Ð Ð Ô Ö Ô Ø Ú Ø Ñ Ø ÓÒ Ó Ô Ø ÓÛ Ø ÛÓÖ Ø Ñ Ø ÓÒ Ó Ñ ÖÓ¹ ÑÙÐ Ø Ú ÓÖ ¾» ¾¾
 ÝØ Ö Ð Ö Ø ÓÒ ØÓÓÐ ÓÖ ÝÒ Ñ ØÖ ÑÙÐ Ø ÓÒ ÙÒÒ Ö Ð ØØ Ö ½ Ë ÔØ Ñ Ö ½¼ ¾¼¼ ½ Ñ ÒÝ Ø Ò ØÓ Ù Ò ÓÖ ÐÔ Ò Û Ø Ø ÑÙÐ Ø ÓÒ ½» ¾¾ ÝØ Ð Ö Ø ÓÒ Ó ÝÒ Ñ ØÖ ÑÙÐ Ø ÓÒ Ó Ø Ú Ñ Ò Ð Ö Ø ÓÒ ÖÓÑ ØÖ ÓÙÒØ Ð Ð Ô Ö Ô Ø Ú Ø Ñ Ø ÓÒ
ÝØ Ö Ð Ö Ø ÓÒ ØÓÓÐ ÓÖ ÝÒ Ñ ØÖ ÑÙÐ Ø ÓÒ ÙÒÒ Ö Ð ØØ Ö ½ Ë ÔØ Ñ Ö ½¼ ¾¼¼ ½ Ñ ÒÝ Ø Ò ØÓ Ù Ò ÓÖ ÐÔ Ò Û Ø Ø ÑÙÐ Ø ÓÒ ½» ¾¾ ÝØ Ð Ö Ø ÓÒ Ó ÝÒ Ñ ØÖ ÑÙÐ Ø ÓÒ Ó Ø Ú Ñ Ò Ð Ö Ø ÓÒ ÖÓÑ ØÖ ÓÙÒØ Ð Ð Ô Ö Ô Ø Ú Ø Ñ Ø ÓÒ
function GENERAL-SEARCH( problem, strategy) returns a solution, or failure initialize the search tree using the initial state of problem loop do if
 ÓÙ ÖÝ ½ ÁÒ ØÖÙØÓÖ³ ÒÓØ ÓÙ ÖÝ ¾ ÁÒ ØÖÙØÓÖ³ ÒÓØ ØÓ ÖØ Ð ÁÒØ ÐÐ Ò ÁÒØÖÓ ÙØ ÓÒ ¹ ËÔÖ Ò ¾¼¼ Ë ÍÊÄ ÛÛÛº ºÙÒк Ù» ÓÙ Öݻ˼ ¹ ¹ º ÓÙ ÖÝ Ë Ù¹Û ¹Ö µ ÖØ ¼¾µ ¾¹ ÓÙ ÖÝ ºÙÒк Ù ØÖ Ø Ý Ò Ý Ô Ò Ø ÓÖ Ö Ó ÒÓ ÜÔ Ò ÓÒ Ì ØÐ
ÓÙ ÖÝ ½ ÁÒ ØÖÙØÓÖ³ ÒÓØ ÓÙ ÖÝ ¾ ÁÒ ØÖÙØÓÖ³ ÒÓØ ØÓ ÖØ Ð ÁÒØ ÐÐ Ò ÁÒØÖÓ ÙØ ÓÒ ¹ ËÔÖ Ò ¾¼¼ Ë ÍÊÄ ÛÛÛº ºÙÒк Ù» ÓÙ Öݻ˼ ¹ ¹ º ÓÙ ÖÝ Ë Ù¹Û ¹Ö µ ÖØ ¼¾µ ¾¹ ÓÙ ÖÝ ºÙÒк Ù ØÖ Ø Ý Ò Ý Ô Ò Ø ÓÖ Ö Ó ÒÓ ÜÔ Ò ÓÒ Ì ØÐ
ÙÖ ¾ Ë Ð Ø ÔÔÐ Ø ÓÒ ¾ ¾
 Å Ë ¹ Í Ö Ù Ú¼º¾ ÔÖ Ð ½¾ ¾¼½¼ ½ ½º½ ÈÖÓ Ø ÉÙÓØ Ì ÕÙÓØ Ð Ø Ò Ö ÐÐÝ ÓÖ Ö Ý Ô Ö Ó Û Ø Ø Ò Û Ø Ø Ø ÓØØÓѺ ÁØ Ñ Ý ÐØ Ö Ý Ð Ø Ò Ò ÔÔÐ Ø ÓÒº ½º½º½ ÉÙÓØ ÉÙÓØ Ò ÔÔÐ ØÓ Ö ÕÙ Ø Ý Ð Ò Ø ÓÒ Ò Ø ÐÐÓ Ø ¹ÓÐÙÑÒ Û Ý ÙÐØ
Å Ë ¹ Í Ö Ù Ú¼º¾ ÔÖ Ð ½¾ ¾¼½¼ ½ ½º½ ÈÖÓ Ø ÉÙÓØ Ì ÕÙÓØ Ð Ø Ò Ö ÐÐÝ ÓÖ Ö Ý Ô Ö Ó Û Ø Ø Ò Û Ø Ø Ø ÓØØÓѺ ÁØ Ñ Ý ÐØ Ö Ý Ð Ø Ò Ò ÔÔÐ Ø ÓÒº ½º½º½ ÉÙÓØ ÉÙÓØ Ò ÔÔÐ ØÓ Ö ÕÙ Ø Ý Ð Ò Ø ÓÒ Ò Ø ÐÐÓ Ø ¹ÓÐÙÑÒ Û Ý ÙÐØ
ÅÓØ Ú Ø ÓÒ Ø Ú Øݹ ØÖ Ú Ð Ñ Ò ÑÓ Ð Ò Ô Ö ÓÒ Ð Þ ÖÚ ÓÒ Ñ ÖØÔ ÓÒ ¾» ¾
 ÅÓ Ð Ò Ø ÝÒ Ñ Ó Ðй Ý Ø Ú ØÝ ÔÐ Ò Ï ÐÐ Ñ À ÑÔ ½ ÙÒÒ Ö Ð ØØ Ö Ê Ö Ó ÀÙÖØÙ Ò Å Ð ÖÐ Ö ¾ ÂÙÒ ¾¾ ¾¼½¼ ½ ÃÍ Ä ÙÚ Ò ¾ È Ä Ù ÒÒ ½» ¾ ÅÓØ Ú Ø ÓÒ Ø Ú Øݹ ØÖ Ú Ð Ñ Ò ÑÓ Ð Ò Ô Ö ÓÒ Ð Þ ÖÚ ÓÒ Ñ ÖØÔ ÓÒ ¾» ¾ ÇÙØÐ Ò
ÅÓ Ð Ò Ø ÝÒ Ñ Ó Ðй Ý Ø Ú ØÝ ÔÐ Ò Ï ÐÐ Ñ À ÑÔ ½ ÙÒÒ Ö Ð ØØ Ö Ê Ö Ó ÀÙÖØÙ Ò Å Ð ÖÐ Ö ¾ ÂÙÒ ¾¾ ¾¼½¼ ½ ÃÍ Ä ÙÚ Ò ¾ È Ä Ù ÒÒ ½» ¾ ÅÓØ Ú Ø ÓÒ Ø Ú Øݹ ØÖ Ú Ð Ñ Ò ÑÓ Ð Ò Ô Ö ÓÒ Ð Þ ÖÚ ÓÒ Ñ ÖØÔ ÓÒ ¾» ¾ ÇÙØÐ Ò
Communications Network Design: lecture 20 p.1/29
 Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¾¼ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð Å Ö ¾ ¾¼¼ Communications Network Design: lecture 20 p.1/29 È È Ø ÓÖ Ö
Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¾¼ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð Å Ö ¾ ¾¼¼ Communications Network Design: lecture 20 p.1/29 È È Ø ÓÖ Ö
Communications Network Design: lecture 19 p.1/32
 Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ½ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð Å Ö ¾ ¾¼¼ Communications Network Design: lecture 19 p.1/32 Æ ØÛÓÖ Ó Ò ØÛÓÖ
Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ½ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð Å Ö ¾ ¾¼¼ Communications Network Design: lecture 19 p.1/32 Æ ØÛÓÖ Ó Ò ØÛÓÖ
Verification. Lecture 3. Bernd Finkbeiner
 Verification Lecture 3 Bernd Finkbeiner Plan for today CTL model checking Thebasicalgorithm Fairness Counterexamplesandwitnesses Review: Computation tree logic modal logic over infinite trees[clarke& Emerson
Verification Lecture 3 Bernd Finkbeiner Plan for today CTL model checking Thebasicalgorithm Fairness Counterexamplesandwitnesses Review: Computation tree logic modal logic over infinite trees[clarke& Emerson
ÁÒØÖÓ ÙØ ÓÒ Ì Ñ Ñ Ö Ó Ú Ò Ô ÓÖ Ù Ô µ Ú Ø Ñ Ò Ö Ð ØÙÖ ÓÒ Ø Ö Ó Ø Ô ØØ ÖÒº ÀÓÛ Ú Ö Ò Ú Ù Ð Ò Ñ Ð Ø ÓÛÒ Ø ÒØ Ñ Ö Ò º Ì Ô ØØ ÖÒ Ö ÒÓØ Ø ÖÑ Ò Ò Ø ÐÐݺ Ì Ý
 Ò Ñ Ð Ó Ø È ØØ ÖÒ ÓÖÑ Ø ÓÒ Ú ÐÝÒ Ë Ò Ö Ô ÖØÑ ÒØ Ó Å Ø Ñ Ø Ð Ë Ò ÓÖ Å ÓÒ ÍÒ Ú Ö ØÝ Ù Ù Ø ¾¼¼½ ÂÓ ÒØ ÛÓÖ Û Ø Ì ÓÑ Ï ÒÒ Ö ÍÅ µ ÁÒØÖÓ ÙØ ÓÒ Ì Ñ Ñ Ö Ó Ú Ò Ô ÓÖ Ù Ô µ Ú Ø Ñ Ò Ö Ð ØÙÖ ÓÒ Ø Ö Ó Ø Ô ØØ ÖÒº ÀÓÛ
Ò Ñ Ð Ó Ø È ØØ ÖÒ ÓÖÑ Ø ÓÒ Ú ÐÝÒ Ë Ò Ö Ô ÖØÑ ÒØ Ó Å Ø Ñ Ø Ð Ë Ò ÓÖ Å ÓÒ ÍÒ Ú Ö ØÝ Ù Ù Ø ¾¼¼½ ÂÓ ÒØ ÛÓÖ Û Ø Ì ÓÑ Ï ÒÒ Ö ÍÅ µ ÁÒØÖÓ ÙØ ÓÒ Ì Ñ Ñ Ö Ó Ú Ò Ô ÓÖ Ù Ô µ Ú Ø Ñ Ò Ö Ð ØÙÖ ÓÒ Ø Ö Ó Ø Ô ØØ ÖÒº ÀÓÛ
Communications Network Design: lecture 07 p.1/44
 Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¼ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð ÔÖ Ð ½ ¾¼¼ Communications Network Design: lecture 07 p.1/44 ÊÓÙØ Ò ÓÒØ
Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¼ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð ÔÖ Ð ½ ¾¼¼ Communications Network Design: lecture 07 p.1/44 ÊÓÙØ Ò ÓÒØ
Communications Network Design: lecture 21 p.1/47
 Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¾½ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð Å Ö ¾ ¾¼¼ Communications Network Design: lecture 21 p.1/47 Ö ÓÒ Ó Ø Ý
Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ¾½ Å ØØ Û ÊÓÙ Ò ÍÒ Ú Ö ØÝ Ó Ð Å Ö ¾ ¾¼¼ Communications Network Design: lecture 21 p.1/47 Ö ÓÒ Ó Ø Ý
½ ÁÒØÖÓ ÙØ ÓÒ Ê ÒØ Ö ÙÐØ Ò ÑÔÐ Ñ ÒØ Ø ÓÒ Ó Ø ÔÐ ÒÒ Ö ½ Ú Ö Ø Ò¹ Ø Ö Ø ÓÖ Ù Ø Ð ÔÔÐ Ð ØÝ Ó Ø ÔÐ ÒÒ Ò ÔÔÖÓ ØÓ Ñ ÒÝ Ö Ð ÛÓÖÐ ÔÖÓ Ð Ñ º ÍÒ ÓÖØÙÒ Ø ÐÝ Ø ÔÖ
 Ò ÜØ Ò ÓÒ Ó Ë ÌÈÄ Æ ÓÖ ÔÐ ÒÒ Ò Û Ø ÓÒ ØÖ ÒØ Å ÖÓ ÓÐ ØØ ËØ ÒÓ Å ÖÙ Ò Ð Ö Ó Å Ð Ò Ô ÖØ Ñ ÒØÓ Å Ø Ñ Ø ÁÒ ÓÖÑ Ø ÍÒ Ú Ö Ø Ð ËØÙ È ÖÙ Î Î ÒÚ Ø ÐÐ ¼ ½¼¼ È ÖÙ ÁØ ÐÝ ¹Ñ Ð Ñ ÖÓ ÒÓ Ñ Ð Ò ÔÑ ØºÙÒ Ô º Ø Ì Ðº ¹¼ ¹ º
Ò ÜØ Ò ÓÒ Ó Ë ÌÈÄ Æ ÓÖ ÔÐ ÒÒ Ò Û Ø ÓÒ ØÖ ÒØ Å ÖÓ ÓÐ ØØ ËØ ÒÓ Å ÖÙ Ò Ð Ö Ó Å Ð Ò Ô ÖØ Ñ ÒØÓ Å Ø Ñ Ø ÁÒ ÓÖÑ Ø ÍÒ Ú Ö Ø Ð ËØÙ È ÖÙ Î Î ÒÚ Ø ÐÐ ¼ ½¼¼ È ÖÙ ÁØ ÐÝ ¹Ñ Ð Ñ ÖÓ ÒÓ Ñ Ð Ò ÔÑ ØºÙÒ Ô º Ø Ì Ðº ¹¼ ¹ º
ÇÙØÐ Ò
 ÀÓÛ ÑÙ ÒØ Ö Ò Ö Ø ÓÒ Ð Ö Ö Ò Ó Ø ÍºËº Ó Ð ÙÖ ØÝ Ý Ø Ñ Ö ÐÐÝ ÔÖÓÚ ½ ½ Ê ¹ Á ÈÖ Ù Å Ý ¾¼½½ ÇÙØÐ Ò ÅÓØ Ú Ø ÓÒ ÓÒÓÑ Ó Ø Ö ÒØ Ò Ö Ø ÓÒ Ö ÒØÐÝ Ä Ñ Ø Ð ØÝ ØÓ Ò ÙÖ Ü¹ ÒØ Ú ¹ ¹Ú ÓØ Ö Ò Ö Ø ÓÒ È Ý¹ ¹ÝÓÙ¹ Ó Ô Ò ÓÒ
ÀÓÛ ÑÙ ÒØ Ö Ò Ö Ø ÓÒ Ð Ö Ö Ò Ó Ø ÍºËº Ó Ð ÙÖ ØÝ Ý Ø Ñ Ö ÐÐÝ ÔÖÓÚ ½ ½ Ê ¹ Á ÈÖ Ù Å Ý ¾¼½½ ÇÙØÐ Ò ÅÓØ Ú Ø ÓÒ ÓÒÓÑ Ó Ø Ö ÒØ Ò Ö Ø ÓÒ Ö ÒØÐÝ Ä Ñ Ø Ð ØÝ ØÓ Ò ÙÖ Ü¹ ÒØ Ú ¹ ¹Ú ÓØ Ö Ò Ö Ø ÓÒ È Ý¹ ¹ÝÓÙ¹ Ó Ô Ò ÓÒ
Ì ÓÑÔÙØ Ð Ñ Ò ÓÒ Ó ÌÖ Ó ÁÒ Ò Ø À Ø ÊÙ ÐÐ Å ÐÐ Ö ÂÙÐÝ ¾ ¾¼¼ Ì Ö Ø ÓÙÖ Ø ÓÒ Ó Ø ÖØ Ð ÔÔ Ö ÔØ Ö Ó È º º Ø Ø Ø ÍÒ Ú Ö ØÝ Ó Ó ÙÒ Ö Ø ÙÔ ÖÚ ÓÒ Ó ÊÓ ÖØ Áº ËÓ
 Ì ÓÑÔÙØ Ð Ñ Ò ÓÒ Ó ÌÖ Ó ÁÒ Ò Ø À Ø ÊÙ ÐÐ Å ÐÐ Ö ÂÙÐÝ ¾ ¾¼¼ Ì Ö Ø ÓÙÖ Ø ÓÒ Ó Ø ÖØ Ð ÔÔ Ö ÔØ Ö Ó È º º Ø Ø Ø ÍÒ Ú Ö ØÝ Ó Ó ÙÒ Ö Ø ÙÔ ÖÚ ÓÒ Ó ÊÓ ÖØ Áº ËÓ Ö º Ì Ò Ö Ð Ó Ù ØÓ ÝÖ Ã ÓÙ ÒÓÚ Û Ó ÓÖ Ò ÐÐÝ ÔÓ Ø ÕÙ
Ì ÓÑÔÙØ Ð Ñ Ò ÓÒ Ó ÌÖ Ó ÁÒ Ò Ø À Ø ÊÙ ÐÐ Å ÐÐ Ö ÂÙÐÝ ¾ ¾¼¼ Ì Ö Ø ÓÙÖ Ø ÓÒ Ó Ø ÖØ Ð ÔÔ Ö ÔØ Ö Ó È º º Ø Ø Ø ÍÒ Ú Ö ØÝ Ó Ó ÙÒ Ö Ø ÙÔ ÖÚ ÓÒ Ó ÊÓ ÖØ Áº ËÓ Ö º Ì Ò Ö Ð Ó Ù ØÓ ÝÖ Ã ÓÙ ÒÓÚ Û Ó ÓÖ Ò ÐÐÝ ÔÓ Ø ÕÙ
Ø ÑÔÐÝ Ù Ø Ø Ø Ø ÔÖÓÓ ÒÓÖÑ Ð Þ Ò Ø ËØÖ Ø ÓÙÒ Ø ÓÒ Ø Ø ÓÖÝ ÔÖ ¹ÑÓ Ð Û Ð Ú Ö ÒØ Ó Ø ÔÖÓÔÓ Ø ÓÒ Ò ØÓ ÔÖÓÚ Ò Ø ÓÖ Ò Ð ÔÖÓÓ º ÁØ ÛÓÖØ ÒÓØ Ò Ø Ø Ø ÓÖ Ò Ð ÒÓ
 Ì ËØÖ Ø ÓÙÒ Ø ÓÒ Ø ÓÖÝ ÑÓ ÙÐÓ ÐÐ ÓÛ ÁÆÊÁ ¹ÊÓÕÙ ÒÓÙÖØ ºÈº ½¼ ½ Ä Ò Ý Ü Ö Ò º ÐÐ º ÓÛ ÒÖ º Ö ØØÔ»»ÐÓ Ðº ÒÖ º Ö» ÓÛ ØÖ Øº Ì ËØÖ Ø ÓÙÒ Ø ÓÒ Ö Ö ØÖ Ø ÓÒ Ó Ò Ú Ø Ø ¹ ÓÖÝ Û Ö Ø ÓÑÔÖ Ò ÓÒ Ñ Ö ØÖ Ø ØÓ ØÖ Ø Ð ÔÖÓÔÓ
Ì ËØÖ Ø ÓÙÒ Ø ÓÒ Ø ÓÖÝ ÑÓ ÙÐÓ ÐÐ ÓÛ ÁÆÊÁ ¹ÊÓÕÙ ÒÓÙÖØ ºÈº ½¼ ½ Ä Ò Ý Ü Ö Ò º ÐÐ º ÓÛ ÒÖ º Ö ØØÔ»»ÐÓ Ðº ÒÖ º Ö» ÓÛ ØÖ Øº Ì ËØÖ Ø ÓÙÒ Ø ÓÒ Ö Ö ØÖ Ø ÓÒ Ó Ò Ú Ø Ø ¹ ÓÖÝ Û Ö Ø ÓÑÔÖ Ò ÓÒ Ñ Ö ØÖ Ø ØÓ ØÖ Ø Ð ÔÖÓÔÓ
 Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ½ Ó Ò ØÛÓÖ Æ ØÛÓÖ ÁÒØ ÖÒ Ø Ò ØÛÓÖ Ó Ò ØÛÓÖ º ÅÓ Ø Ó Ø Ì Å ØØ Û ÊÓÙ Ò Û Ú ÓÒ Ö ÙÔ ØÓ Ø ÔÓ ÒØ ÓÒ ÖÒ ÔÖÓ
Ó ÔÔÐ Å Ø Ñ Ø ÔÐ Ò Ó Å Ø Ñ Ø Ð Ë Ò Ë ÓÓÐ ÓÑÑÙÒ Ø ÓÒ Æ ØÛÓÖ Ò Ð ØÙÖ ½ Ó Ò ØÛÓÖ Æ ØÛÓÖ ÁÒØ ÖÒ Ø Ò ØÛÓÖ Ó Ò ØÛÓÖ º ÅÓ Ø Ó Ø Ì Å ØØ Û ÊÓÙ Ò Û Ú ÓÒ Ö ÙÔ ØÓ Ø ÔÓ ÒØ ÓÒ ÖÒ ÔÖÓ
Ö Ô ÓÒ Ø Ó ØÛÓ Ø Î Ò ÒÓØ Ý Î µº Ë Ø Î Ò Ø ÒÓÒ¹ ÑÔØÝ Ø Ó Ú ÖØ ÓÖ ÒÓ µ Ò Ø Ó Ô Ö Ó Ú ÖØ ÐÐ º Ï Ù Î µ Ò µ ØÓ Ö ÔÖ ÒØ Ø Ø Ó Ú ÖØ Ò Ò Ö Ô Ö Ô Ø Ú Ðݺ ÅÓÖ Ò
 Ö Ô Ð ÓÖ Ø Ñ ÁÒ ½ ÙÐ Ö Ú Ø Ø ÖÒ ÈÖÙ Ò ÃÓ Ò Ö Ò ÓÙÒ Ø Ö Û Ö Ú Ò Ö ÖÓ Ø Ö Ú Ö Ò Ò Ð Ò º À Ñ ÙÔ ÕÙ Ø ÓÒ Ø Ø Ò ÒÝÓÒ Ø ÖØ Ø ÒÝ Ð Ò µ Û Ð Ø ÖÓÙ Ü ØÐÝ ÓÒ ÓÖ Ö Ò Ö ØÙÖÒ ØÓ Ø ÓÖ ¹ Ò Ð Ø ÖØ Ò ÔÓ ÒØ Ê Ö ØÓ ÙÖ ½º
Ö Ô Ð ÓÖ Ø Ñ ÁÒ ½ ÙÐ Ö Ú Ø Ø ÖÒ ÈÖÙ Ò ÃÓ Ò Ö Ò ÓÙÒ Ø Ö Û Ö Ú Ò Ö ÖÓ Ø Ö Ú Ö Ò Ò Ð Ò º À Ñ ÙÔ ÕÙ Ø ÓÒ Ø Ø Ò ÒÝÓÒ Ø ÖØ Ø ÒÝ Ð Ò µ Û Ð Ø ÖÓÙ Ü ØÐÝ ÓÒ ÓÖ Ö Ò Ö ØÙÖÒ ØÓ Ø ÓÖ ¹ Ò Ð Ø ÖØ Ò ÔÓ ÒØ Ê Ö ØÓ ÙÖ ½º
Ø Ñ Ò Ò ÙØÙÑÒ ¾¼¼¾ Ò Ò Ö ÕÙ ÒØ ÐÓ µ Ø Û Ø ØÖ ØÖÙØÙÖ ½ ȹØÖ È¹ ÖÓÛØ ÄÇË Ì È¹ØÖ Ø ØÖÙØÙÖ È¹ ÖÓÛØ Ð ÓÖ Ø Ñ ÓÖ Ò Ò ÐÐ Ö ÕÙ ÒØ Ø ÄÇË Ì Ð ÓÖ Ø Ñ ÓÖ Ò Ò Ö ÕÙ
 Ø Ñ Ò Ò ÙØÙÑÒ ¾¼¼¾ Ò Ò Ö ÕÙ ÒØ ÐÓ µ Ø Û Ø ØÖ ØÖÙØÙÖ ½ Ö ÕÙ ÒØ ÐÓ µ Ø Û Ø Ò Ò ØÖÙØÙÖ ØÖ Ø Ñ Ò Ò ÙØÙÑÒ ¾¼¼¾ Ò Ò Ö ÕÙ ÒØ ÐÓ µ Ø Û Ø ØÖ ØÖÙØÙÖ ½ ȹØÖ È¹ ÖÓÛØ ÄÇË Ì È¹ØÖ Ø ØÖÙØÙÖ È¹ ÖÓÛØ Ð ÓÖ Ø Ñ ÓÖ Ò Ò ÐÐ
Ø Ñ Ò Ò ÙØÙÑÒ ¾¼¼¾ Ò Ò Ö ÕÙ ÒØ ÐÓ µ Ø Û Ø ØÖ ØÖÙØÙÖ ½ Ö ÕÙ ÒØ ÐÓ µ Ø Û Ø Ò Ò ØÖÙØÙÖ ØÖ Ø Ñ Ò Ò ÙØÙÑÒ ¾¼¼¾ Ò Ò Ö ÕÙ ÒØ ÐÓ µ Ø Û Ø ØÖ ØÖÙØÙÖ ½ ȹØÖ È¹ ÖÓÛØ ÄÇË Ì È¹ØÖ Ø ØÖÙØÙÖ È¹ ÖÓÛØ Ð ÓÖ Ø Ñ ÓÖ Ò Ò ÐÐ
CMD MDS Recovery DLD
 CMD MDS Recovery DLD Mike Pershin February 6, 2008 1 Introduction This document describes recovery changes in CMD. 2 Requirements The CMD environment requires the reviewed recovery due to major changes
CMD MDS Recovery DLD Mike Pershin February 6, 2008 1 Introduction This document describes recovery changes in CMD. 2 Requirements The CMD environment requires the reviewed recovery due to major changes
ÇÙØÐ Ò ½ Ï Ø ØÓ ØÙ Ý ÓÙØ ÐØ ² ÙÖ ¾ ÓÐÓ Ð ÅÓ Ð ÐÓÓ Ø Ø ÓÖ Ø À Ö Ö Ð ÅÓ Ð Ò Ú Ù Ð Æ ÖÓÙÔ ÐÓÛ Ò ÐÝ ØÓÓÐ ØÓ ØÙ Ý ÑÓÚ Ñ ÒØ Ù ÓÒ Å Ö Ð Ë ÖÚ Ð Ó À ÐØ ² ÍÖ ÈÁ
 À ÐØ ² ÍÖ Ñ Ø Ó ØÓ ÒÚ Ø Ø ÐØ Ò ÙÖ Ò Ô Å Ö Ð Ë ÖÚ Ð Ó ÙÒ Ó Ç Û Ð Ó ÖÙÞ ÈÖÓ Ö Ñ ÓÑÔÙØ Ó ÒØ ÓÐ Æ ÓÒ Ð Ë È Ð ÈÁ ¾¼¼ Å Ö Ð Ë ÖÚ Ð Ó À ÐØ ² ÍÖ ÈÁ ¾¼¼ ½» ½ ÇÙØÐ Ò ½ Ï Ø ØÓ ØÙ Ý ÓÙØ ÐØ ² ÙÖ ¾ ÓÐÓ Ð ÅÓ Ð ÐÓÓ Ø
À ÐØ ² ÍÖ Ñ Ø Ó ØÓ ÒÚ Ø Ø ÐØ Ò ÙÖ Ò Ô Å Ö Ð Ë ÖÚ Ð Ó ÙÒ Ó Ç Û Ð Ó ÖÙÞ ÈÖÓ Ö Ñ ÓÑÔÙØ Ó ÒØ ÓÐ Æ ÓÒ Ð Ë È Ð ÈÁ ¾¼¼ Å Ö Ð Ë ÖÚ Ð Ó À ÐØ ² ÍÖ ÈÁ ¾¼¼ ½» ½ ÇÙØÐ Ò ½ Ï Ø ØÓ ØÙ Ý ÓÙØ ÐØ ² ÙÖ ¾ ÓÐÓ Ð ÅÓ Ð ÐÓÓ Ø
Kevin Dowd, after his book High Performance Computing, O Reilly & Associates, Inc, 1991
 Ò Û Ö ÌÓ ÉÙ Ø ÓÒ ÁÒ Ï ÐÐ ÝÓÒ ÆÙÑÈÝ Ö Ð Ò Ú ÐÓÔ Ö Ò ÈÝÌ Ð Ö ØÓÖ ÂÙÐÝ Ø ¹½½Ø ¾¼½¼º È Ö ¹ Ö Ò ÇÙØÐ Ò Ì Ø Á Ù Ò Û Ö ÌÓ ÉÙ Ø ÓÒ ÁÒ ½ Ì Ø Á Ù ¾ Ò Û Ö ÌÓ ÉÙ Ø ÓÒ ÁÒ ÇÙØÐ Ò Ì Ø Á Ù Ò Û Ö ÌÓ ÉÙ Ø ÓÒ ÁÒ ½ Ì Ø Á
Ò Û Ö ÌÓ ÉÙ Ø ÓÒ ÁÒ Ï ÐÐ ÝÓÒ ÆÙÑÈÝ Ö Ð Ò Ú ÐÓÔ Ö Ò ÈÝÌ Ð Ö ØÓÖ ÂÙÐÝ Ø ¹½½Ø ¾¼½¼º È Ö ¹ Ö Ò ÇÙØÐ Ò Ì Ø Á Ù Ò Û Ö ÌÓ ÉÙ Ø ÓÒ ÁÒ ½ Ì Ø Á Ù ¾ Ò Û Ö ÌÓ ÉÙ Ø ÓÒ ÁÒ ÇÙØÐ Ò Ì Ø Á Ù Ò Û Ö ÌÓ ÉÙ Ø ÓÒ ÁÒ ½ Ì Ø Á
½º ÌÖ ÙØÓÑØ
 ÄÒÙ ÓÖÑÐ Ò ÙØÓÑØ ÌÓÖÝ Å Ó Ë ½½ ½º ÌÖ ÙØÓÑØ ËØ Ó ÙÒØÓÒ ÝÑÓÐ ÛØ ÖÒ ÖØÝ Ó ÖØÝ Æ ÆÙÑÖ ËØ Ì µ Ó ØÖÑ ÅÒÑÐ Ø Ø Ý Ò ¾ Ì µ ººº Ü ¾ Ü ¾ Ì µ ººº ¾ Ò ÖØÝ µ ¼ ½ Ø Ò µ ¾ Ì µ Ø ¾ ÖØÝ µ Ò Ø ¾ Ì µ ººº Ó ØÖÑ µ µ ܺ ËØ Ì
ÄÒÙ ÓÖÑÐ Ò ÙØÓÑØ ÌÓÖÝ Å Ó Ë ½½ ½º ÌÖ ÙØÓÑØ ËØ Ó ÙÒØÓÒ ÝÑÓÐ ÛØ ÖÒ ÖØÝ Ó ÖØÝ Æ ÆÙÑÖ ËØ Ì µ Ó ØÖÑ ÅÒÑÐ Ø Ø Ý Ò ¾ Ì µ ººº Ü ¾ Ü ¾ Ì µ ººº ¾ Ò ÖØÝ µ ¼ ½ Ø Ò µ ¾ Ì µ Ø ¾ ÖØÝ µ Ò Ø ¾ Ì µ ººº Ó ØÖÑ µ µ ܺ ËØ Ì
Plot A. Plot B. Plot D. Plot C
 Ï Ò Ó Ø ÒØ ÓÑÔÓÒ ÒØ Ö Ò ÙÒ Ø Ð ØÝ Å Ð ÅÓÐÐÓÝ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó ÌÓÖÓÒØÓ ÌÓÖÓÒØÓ Ò Å Ö ¼¼ ØÖ Ø Ï ØÙ Ý Ö Ò ÓÑ ÓÒ ØÖ ÒØ Ø Ø ÓÒ ÔÖÓ Ð Ñ Ù Ò Ø Û Ð Ó ÑÓ Ð ÒØÖÓ Ù Ý Ø ÙØ ÓÖ Û ÒÐÙ Ú Ö ÓÙ ÓÖÑ Ó
Ï Ò Ó Ø ÒØ ÓÑÔÓÒ ÒØ Ö Ò ÙÒ Ø Ð ØÝ Å Ð ÅÓÐÐÓÝ Ô ÖØÑ ÒØ Ó ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó ÌÓÖÓÒØÓ ÌÓÖÓÒØÓ Ò Å Ö ¼¼ ØÖ Ø Ï ØÙ Ý Ö Ò ÓÑ ÓÒ ØÖ ÒØ Ø Ø ÓÒ ÔÖÓ Ð Ñ Ù Ò Ø Û Ð Ó ÑÓ Ð ÒØÖÓ Ù Ý Ø ÙØ ÓÖ Û ÒÐÙ Ú Ö ÓÙ ÓÖÑ Ó
ËÌ Ä Å Ä Å ÌÁÇÆ ÂÓ Ò Ìº Ð Û Ò Ô ÖØÑ ÒØ Ó Å Ø Ñ Ø ËØ Ø Ø Ò ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó ÁÐÐ ÒÓ Ø Ó Â ÒÙ ÖÝ ¾¼¼¼ Ø ØÓ Ø Ñ ÑÓÖÝ Ó ºÁºÅ Ð Úº ÁÒ ½ ÖÞ ÓÖÞÝ Û Ø Ö
 ËÌ Ä Å Ä Å ÌÁÇÆ ÂÓ Ò Ìº Ð Û Ò Ô ÖØÑ ÒØ Ó Å Ø Ñ Ø ËØ Ø Ø Ò ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó ÁÐÐ ÒÓ Ø Ó Â ÒÙ ÖÝ ¾¼¼¼ Ø ØÓ Ø Ñ ÑÓÖÝ Ó ºÁºÅ Ð Úº ÁÒ ½ ÖÞ ÓÖÞÝ Û Ø Ö Ø Ö Û Ö ÓÒØ ÒÙÙÑ Ñ ÒÝ «Ö ÒØ ¼ ¹ Ø ÓÖ Ð Ø ÓÖ º Ï Ø
ËÌ Ä Å Ä Å ÌÁÇÆ ÂÓ Ò Ìº Ð Û Ò Ô ÖØÑ ÒØ Ó Å Ø Ñ Ø ËØ Ø Ø Ò ÓÑÔÙØ Ö Ë Ò ÍÒ Ú Ö ØÝ Ó ÁÐÐ ÒÓ Ø Ó Â ÒÙ ÖÝ ¾¼¼¼ Ø ØÓ Ø Ñ ÑÓÖÝ Ó ºÁºÅ Ð Úº ÁÒ ½ ÖÞ ÓÖÞÝ Û Ø Ö Ø Ö Û Ö ÓÒØ ÒÙÙÑ Ñ ÒÝ «Ö ÒØ ¼ ¹ Ø ÓÖ Ð Ø ÓÖ º Ï Ø
Backoff DOP: Parameter Estimation by Backoff
 Backoff DOP: Parameter Estimation by Backoff Luciano Buratto and Khalil ima an Institute for Logic, Language and Computation (ILLC) University of Amsterdam, Amsterdam, The Netherlands simaan@science.uva.nl;
Backoff DOP: Parameter Estimation by Backoff Luciano Buratto and Khalil ima an Institute for Logic, Language and Computation (ILLC) University of Amsterdam, Amsterdam, The Netherlands simaan@science.uva.nl;
 Ð Ø ÓÖ Ê Ö Ò Å ÒÙ Ð ½º¼ ÐÔ Ò Ö Ø Ý ÓÜÝ Ò ½º º º½ Ï ½ ¼¼ ½ ¾½ ¾¼¼ ÓÒØ ÒØ ½ Ð Ø ÓÖ Å Ò È ½ ½º½ ÁÒØÖÓ ÙØ ÓÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾ Ð Ø ÓÖ Ø ËØÖÙØÙÖ
Ð Ø ÓÖ Ê Ö Ò Å ÒÙ Ð ½º¼ ÐÔ Ò Ö Ø Ý ÓÜÝ Ò ½º º º½ Ï ½ ¼¼ ½ ¾½ ¾¼¼ ÓÒØ ÒØ ½ Ð Ø ÓÖ Å Ò È ½ ½º½ ÁÒØÖÓ ÙØ ÓÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾ Ð Ø ÓÖ Ø ËØÖÙØÙÖ
½º¾ Ò Ø ÓÒ Ì Ò Ó Ø ÓÚ ÕÙ Ø ÓÒ Ò ÓÖÑ Ð Þ Ý Ø ÓÐÐÓÛ Ò Ò Ø ÓÒº Ò Ø ÓÒ ½ È Ù Ó Ê Ò ÓÑ ÙÒØ ÓÒ Ñ Ðݵ Ñ ÐÝ ¾ ¼ ½ ¾Æ ÐÐ Ñ ÐÝ Ó Ð µ Ä µµ È Ù Ó Ê Ò ÓÑ ÙÒØ ÓÒ ¾
 ¾¾º ¼ ¹¼¼ ÁÒØÖÓ ÙØ ÓÒ ØÓ ÖÝÔØÓ Ö Ô Ý ÆÓÚ Ñ Ö Ø ¾¼¼½ Ä ØÙÖ Ä ØÙÖ Ö Ú Ò Ý Ó ËÖ ÒØÓÒ Ó Æ ÓÐÓ Ä Ø Ø Ñ Û Ò Û Ø Û Ñ Ò Ý Ë Ö Ø Ã Ý ÒÖÝÔØ ÓÒ Ñ Ëà µ Ò Û ÒØÖÓ Ù ØÛÓ Ö Ð Ø ÒÓØ ÓÒ Ó ÙÖ Øݺ Ì Ò Û ÓÛ ÓÛ ÈÊ Ñ Ý Ù ØÓ
¾¾º ¼ ¹¼¼ ÁÒØÖÓ ÙØ ÓÒ ØÓ ÖÝÔØÓ Ö Ô Ý ÆÓÚ Ñ Ö Ø ¾¼¼½ Ä ØÙÖ Ä ØÙÖ Ö Ú Ò Ý Ó ËÖ ÒØÓÒ Ó Æ ÓÐÓ Ä Ø Ø Ñ Û Ò Û Ø Û Ñ Ò Ý Ë Ö Ø Ã Ý ÒÖÝÔØ ÓÒ Ñ Ëà µ Ò Û ÒØÖÓ Ù ØÛÓ Ö Ð Ø ÒÓØ ÓÒ Ó ÙÖ Øݺ Ì Ò Û ÓÛ ÓÛ ÈÊ Ñ Ý Ù ØÓ
ËÓÙÖ Ö Ø Ò Ö³ Ó Ø ÓÒ Ò ÐÓÓÑ Ö
 ÀÓÛ ÝÑÑ ØÖÝ Ó ÁÒ ÓÖÑ Ø ÓÒ Ô Ø Ä Ò Ò ÒÒ Ð È Ö Ë ÓÓÐ Ó ÓÒÓÑ ² ÍÒ Ú Ö Ø È Ö ½ È ÒØ ÓÒ ËÓÖ ÓÒÒ ÒÒÙ Ð É Å Ø Ò ËÓÙÖ Ö Ø Ò Ö³ Ó Ø ÓÒ Ò ÐÓÓÑ Ö ÅÓØ Ú Ø ÓÒ ÁÁ Ø Ö Ø ÓÐÐ Ô Ó Ä Ñ ÒÒ ÖÓØ Ö Ä Ö ÒÖ Ó Ø ÔÖ ØÛ Ò Ø ÙÒ Ê
ÀÓÛ ÝÑÑ ØÖÝ Ó ÁÒ ÓÖÑ Ø ÓÒ Ô Ø Ä Ò Ò ÒÒ Ð È Ö Ë ÓÓÐ Ó ÓÒÓÑ ² ÍÒ Ú Ö Ø È Ö ½ È ÒØ ÓÒ ËÓÖ ÓÒÒ ÒÒÙ Ð É Å Ø Ò ËÓÙÖ Ö Ø Ò Ö³ Ó Ø ÓÒ Ò ÐÓÓÑ Ö ÅÓØ Ú Ø ÓÒ ÁÁ Ø Ö Ø ÓÐÐ Ô Ó Ä Ñ ÒÒ ÖÓØ Ö Ä Ö ÒÖ Ó Ø ÔÖ ØÛ Ò Ø ÙÒ Ê
ØÓ ÓÑÔ Ö Ø Ñ ÓÛ ØÓ Ò Ö Ø Ø Ñ ÓÛ º º ÓÙ ÖÝ ¾ ÁÒ ØÖÙØÓÖ³ ÒÓØ ÇÙØÐ Ò Ø ÓÖ Þ Ø ÓÒ Ó Ö Ø Ò ÕÙ ÇÖ Ö Ö Ö Û Ø Ò Ú ÐÙ Ø ÓÒ ÙÒØ ÓÒµ ع Ö Ø Ö Ö Ý Ö ½µ Ñ Ð ÙÖ Ø Ù
 Ö Ò ÁÅ ÔØ Ö Ë Ø ÓÒ º º µ Ê ÕÙ Ö ÔØ Ö ½¼ ½ Ò ½ º ÄÏÀ ØÓ ÖØ Ð ÁÒØ ÐÐ Ò ÁÒØÖÓ ÙØ ÓÒ ¹ ËÔÖ Ò ¾¼½ Ë º ÓÙ ÖÝ Ë Ù¹Û ¹Ö µ ÖØ ¼¾µ ¾¹ º º ÓÙ ÖÝ ½ ÁÒ ØÖÙØÓÖ³ ÒÓØ ÁÒ ÓÖÑ Ë Ö Å Ø Ó Ì ØÐ ÍÊÄ ÛÛÛº ºÙÒк Ù» ÓÙ Öݻ˽ ¹
Ö Ò ÁÅ ÔØ Ö Ë Ø ÓÒ º º µ Ê ÕÙ Ö ÔØ Ö ½¼ ½ Ò ½ º ÄÏÀ ØÓ ÖØ Ð ÁÒØ ÐÐ Ò ÁÒØÖÓ ÙØ ÓÒ ¹ ËÔÖ Ò ¾¼½ Ë º ÓÙ ÖÝ Ë Ù¹Û ¹Ö µ ÖØ ¼¾µ ¾¹ º º ÓÙ ÖÝ ½ ÁÒ ØÖÙØÓÖ³ ÒÓØ ÁÒ ÓÖÑ Ë Ö Å Ø Ó Ì ØÐ ÍÊÄ ÛÛÛº ºÙÒк Ù» ÓÙ Öݻ˽ ¹
½½ º º À Æ Æ º º Í Æ ÒÓØ ÔÓ Ø Ú Ñ ¹ Ò Ø ÙÒÐ Ø ÓÐÐÓÛ Ò ØÖÙ Ø Ö ÓÒ Ù ÔÖÓ Ð Ñ È ½ Û Ø Ò Ð ÐÐ ÓÒ ØÖ ÒØ Û Ó ÓÖÑ Ù Ø ØÓ Ñ Ò ¾Ê Ò µ ½ ¾ Ì Ì Ø Ì Ù ÔÖÓ Ð Ñ Ø Ð
 ÂÓÙÖÒ Ð Ó ÓÑÔÙØ Ø ÓÒ Ð Å Ø Ñ Ø ÎÓк½ ÆÓº¾ ¾¼¼½ ½½ ß½¾ º ÇÆ Å ÁÅ Ç Í Ä ÍÆ ÌÁÇÆ Ç ÌÀ Ì ËÍ ÈÊÇ Ä Å ½µ ÓÒ ¹ Ò Ê Ö Ú ÐÓÔÑ ÒØ ÒØ Ö Ó È Ö ÐÐ Ð ËÓ ØÛ Ö ÁÒ Ø ØÙØ Ó ËÓ ØÛ Ö Ò ½¼¼¼ ¼ Ò µ ¹Ü Ò Ù Ò ËØ Ø Ã Ý Ä ÓÖ ØÓÖÝ
ÂÓÙÖÒ Ð Ó ÓÑÔÙØ Ø ÓÒ Ð Å Ø Ñ Ø ÎÓк½ ÆÓº¾ ¾¼¼½ ½½ ß½¾ º ÇÆ Å ÁÅ Ç Í Ä ÍÆ ÌÁÇÆ Ç ÌÀ Ì ËÍ ÈÊÇ Ä Å ½µ ÓÒ ¹ Ò Ê Ö Ú ÐÓÔÑ ÒØ ÒØ Ö Ó È Ö ÐÐ Ð ËÓ ØÛ Ö ÁÒ Ø ØÙØ Ó ËÓ ØÛ Ö Ò ½¼¼¼ ¼ Ò µ ¹Ü Ò Ù Ò ËØ Ø Ã Ý Ä ÓÖ ØÓÖÝ
The Effectiveness of Receipt-Based Attacks on ThreeBallot
 The Effectiveness of Receipt-Based Attacks on ThreeBallot Kevin Henry, Douglas R. Stinson, Jiayuan Sui David R. Cheriton School of Computer Science University of Waterloo Waterloo, N, N2L 3G1, Canada {k2henry,
The Effectiveness of Receipt-Based Attacks on ThreeBallot Kevin Henry, Douglas R. Stinson, Jiayuan Sui David R. Cheriton School of Computer Science University of Waterloo Waterloo, N, N2L 3G1, Canada {k2henry,
ÅÓØ Ú Ø ÓÒ ØÓ Ø ÕÙ Ù Ò ÑÓ Ð Ó ØÖ ÓÛ ÑÓ Ð Ò Ó Ö ¹ Ú Ö ØÖ Ú Ð Ú ÓÖ Ò ÐÝ Ó Ò ØÛÓÖ Ö ÓÛÒ ÓÑÔÙØ Ø ÓÒ Ó ÜÔ Ø Ú ÐÙ ººº Ô Ø ÖÓÙ Ö ÒØ Ð ÕÙ Ø ÓÒ Ð Ò Ö Þ Ø ÓÒ Ó
 ÝÒ Ñ Ò ØÛÓÖ ÐÓ Ò ØÓ Ø Ö ÒØ Ð ÑÓ Ð Ø Ø Ö Ú Ð Ò Ø Ø ØÖ ÙØ ÓÒ ÖÓÐ Ò Ç ÓÖ Ó ÅÁ̵ ÙÒÒ Ö Ð ØØ Ö ÃÌÀµ Å Ð ÖÐ Ö È Äµ ÂÙÐÝ ½ ¾¼½½ ½» ¾ ÅÓØ Ú Ø ÓÒ ØÓ Ø ÕÙ Ù Ò ÑÓ Ð Ó ØÖ ÓÛ ÑÓ Ð Ò Ó Ö ¹ Ú Ö ØÖ Ú Ð Ú ÓÖ Ò ÐÝ Ó Ò ØÛÓÖ
ÝÒ Ñ Ò ØÛÓÖ ÐÓ Ò ØÓ Ø Ö ÒØ Ð ÑÓ Ð Ø Ø Ö Ú Ð Ò Ø Ø ØÖ ÙØ ÓÒ ÖÓÐ Ò Ç ÓÖ Ó ÅÁ̵ ÙÒÒ Ö Ð ØØ Ö ÃÌÀµ Å Ð ÖÐ Ö È Äµ ÂÙÐÝ ½ ¾¼½½ ½» ¾ ÅÓØ Ú Ø ÓÒ ØÓ Ø ÕÙ Ù Ò ÑÓ Ð Ó ØÖ ÓÛ ÑÓ Ð Ò Ó Ö ¹ Ú Ö ØÖ Ú Ð Ú ÓÖ Ò ÐÝ Ó Ò ØÛÓÖ
