Seminar on Applications of Mathematics: Voting. EDB Hong Kong Science Museum,
|
|
|
- Willis Day
- 5 years ago
- Views:
Transcription
1 Seminar on pplications of Mathematics: Voting ED Hong Kong Science Museum, Ng Tuen Wai, Department of Mathematics, HKU
2 Outline Examples of voting system What should be an ideal voting system? rrow's Impossibility Theorem Main idea of the proof of rrow's Impossibility Theorem Yes-no voting systems and the dimension of these systems. How to quantify political power? Examples of power indices and their applications to the LEGO voting system.
3 Simple majority vote for two candidates When there are only two candidates or alternatives, we can simply use the simple majority vote. The situation is much more complicated if we have at least three candidates or alternatives.
4 Voting Paradox Suppose we have three candidates,, and, and that there are three voters with preferences as follows: Voter 1: > > Voter 2: >> Voter 3: >> For vs, wins (2 to 1) For vs, wins (2 to 1) For vs, wins (2 to 1) Therefore, the requirement of majority rule then provides no clear winner. This is paradoxical, because it means that majority wishes can be in conflict with each other.
5 Individual Preferences D E M F M F E M Social hoice Theory Voting System or Social hoice Procedure Social choice theory studies a given voting system or social choice procedure and describe how individual preferences are aggregated to form a collective preference. Vote Outcome or Social hoice/social hoice List D F M
6 Who is your favorite hero? E D
7 What is your preference? My preference list is > D > > > E How to determine who is the most popular hero?
8 Example 1: Suppose we have 55 students and assume their preferences are recorded in the following table. hoice students st hoice D E E 2 nd hoice D E 3 rd hoice E D E E D D 4 th hoice D 5 th hoice
9 How to determine who is the most popular hero? Individual Preferences D D E E E D Voting System or Social hoice Procedure Vote Outcome or Social hoice D E We shall illustrate the five common social choice procedures with this single example.
10 Social hoice Procedure 1: Plurality Voting Plurality voting is the social choice procedure that most directly generalizes the idea of simple majority vote from the easy case of two candidates to the complicated case of three or more candidates. The idea is simply to declare as the social choice(s) the candidate with the largest number of first-place rankings in the individual preference lists.
11 Social hoice Procedure 1: Plurality Voting hoice students st hoice D E E 2 nd hoice D E 3 rd hoice E D E E D D 4 th hoice D 5 th hoice Since candidate occurs at the top of the most lists(18), it is the social choice when the plurality method is used.
12 Social hoice Procedure 2: The orda ount First introduced by Jean-harles de orda in 1781, the social choice procedure known as the orda count. It is popular in situations where one really wants to take advantage of the information regarding individual intensity of preference provided by looking at how high up in an individual s preference list of a given candidate occurs.
13 Social hoice Procedure 2: The orda ount More precisely, one uses each preference list to award points to each of n candidates as follows: the candidate at the bottom of the list gets one points, the candidate at the next to the bottom spot gets two points and so on up to the top candidate on the list which gets n points. For each candidate, we simply add up the points awarded it from each of the individual preference lists. The candidate(s) with the highest score is declared to be the social choice.
14 hoice 1 st hoice 2 nd hoice 3 rd hoice 4 th hoice 5 th hoice students 18 D E 12 E D 10 : (5) (18) + (1) ( ) = 127 : (5) (12) + (4) (10 + 4) + (2) (2 + 9) + (1) (18) = 156 : (5) (10) + (4) (9 + 2) + (2) ( ) = 162 D : (5) (9) + (4) (18) + (3) ( ) + (2) + (10) = 191 E : (5) (4 + 2) + (4) (12) + (3) ( ) = 189 andidate D wins! E D 9 D E 4 E D 2 E D
15 Social hoice Procedure 3: The Hare System The Hare procedure was introduced by Thomas Hare in 1861, and is also known as the single transferable vote system. In 1862, John Stuart Mill spoke of it as being among the greatest improvements yet made in the theory and practice of government. Today, it is used to elect public officials in ustralia, Malta, The Republic of Ireland, and Northern Ireland.
16 The Hare system is based on the idea of arriving at a social choice by successive deletions of less desirable candidates. More precisely, the procedure is as follows. If any candidate occurs at the top of at least half the preference lists, then it is declared to be the social choice (or at least tied for such), and the process is completed. If no candidate is on top of half of the lists, then we select the candidate(s) occurring at the top of the fewest lists and we delete this (these) particular candidate(s) from each of the preference lists.
17 Social hoice Procedure 3: The Hare System t this stage we have lists that are at least one candidate shorter than that with which we started. Now, we simply repeat the same process for the revised list. The procedure stops when either some candidate is on top of at least half of the (shortened) lists, or when all the remaining candidates occur at the top of exactly the same number of lists (in which case this set of candidates is declared to be the social choice set).
18 hoice students st hoice D E E 2 nd hoice D E 3 rd hoice E D E E D D 4 th hoice D 5 th hoice Since there are 55 students, at least 28 are needed for a majority. Notice that no candidate is on top of at least 28 of the lists, we therefore delete the candidate which is on top of the fewest lists. Delete andidate E!
19 hoice students st hoice D 2 nd hoice D D D D 3 rd hoice D 4 th hoice D gain no candidate is on top of at least 28 of the lists, we therefore delete the candidate which is on top of the fewest lists. Delete andidate D!
20 hoice students st hoice 2 nd hoice 3 rd hoice gain no candidate is on top of at least 28 of the lists, we therefore delete the candidate which is on top of the fewest lists. Delete andidate!
21 hoice students st hoice 2 nd hoice Since candidate is on top of at least 28 of the lists, candidate is the social choice when the Hare procedure is used. andidate wins!
22 Social hoice Procedure 4: Sequential Pairwise Voting with a Fixed genda We have a fixed ordering of the candidates [,,,... ] called the agenda. The first candidate in the ordering is pitted against the second in the kind of one-on-one contest. The winning candidate (or both, if there is a tie) is then pitted against the third candidate in the list in a one-on-one contest.
23 Social hoice Procedure 4: Sequential Pairwise Voting with a Fixed genda candidate is deleted at the end of any round in which it loses a one-on-one contest. The process is continued along the agenda until the survivors have finally met the last candidate in the agenda. Those remaining at the end are declared to be the social choices.
24 hoice students st hoice D E E 2 nd hoice D E 3 rd hoice E D E E D D 4 th hoice D 5 th hoice vs : Since > is equal to 18, wins and we delete. vs : Since > is equal to 16, wins and we delete. vs D: Since > D is equal to 12, D wins and we delete. D vs E: Since D > E is equal to 27, E wins and we delete D. andidate E wins!
25 We have seen that for candidate, D, and E, there is at least one social choice procedure or voting system making it the social choice. Is there a voting system making (Wonder Woman) the social choice?
26 Social hoice Procedure 5: Dictatorship hoose one of the people, say p and call this person p the dictator. The procedure now runs as follows. Given the sequence of individual preference lists, we simply ignore all the lists except that of the dictator p. The candidate on top of p's list is now declared to be the social choice.
27 hoice students st hoice D E E 2 nd hoice D E 3 rd hoice E D E E D D 4 th hoice D 5 th hoice There are 12 students whose preference list is > E > D > >. Pick any one of the 12 students to be the dictator, then the social choice is simply the candidate on top of his list, namely candidate. andidate wins!
28 Which social choice procedure should we use? Our five examples of social choice procedure yield five different social choices when confronted by these particular preference list. This raises the question of whether some procedures might be strictly better than others. ut better in what ways?
29 Four desirable properties of social choice procedure Pareto ondition Independence of irrelevant candidates/alternatives (II/II) Monotonicity Nondictatorship
30 Who is Kenneth rrow? Kenneth Joseph rrow is an merican economist who was considered as the founder of modern voting theory or social choice theory He was awarded the Nobel Prize in Economics in 1972 on his work in social choice theory. (1921--)
31 Who is Kenneth rrow? In 1950, he proved the celebrated rrow's Impossibility Theorem in the paper " Difficulty in the oncept of Social Welfare", Journal of Political Economy 58(4) (ugust, 1950), pp He was then awarded a PhD thesis from olumbia University in 1951.
32 What is rrow's Impossibility Theorem? rrow's theorem can be loosely interpreted as no voting method is ideal. More precisely, if there are more than three candidates to choose from, no voting method can convert the preferences of individuals to a community-wide ranking, while also meeting the four desirable criteria.
33 rrow's Impossibility Theorem Theorem (rrow, 1950) ny social choice procedure for more than two candidates satisfying the Pareto condition, independence of irrelevant candidates, and monotonicity is a dictatorship. orollary There is no social choice procedure for more than two candidates satisfying the Pareto condition, independence of irrelevant candidates, monotonicity and nondictatorship.
34 Four Desirable riteria We will use the notation > to denote is ranked above. Pareto ondition If > in all individual preference lists, then > in the social preference list. [ If everyone prefers to, then the society prefers to.]
35 Pareto ondition If a > b in all individual preference lists, then a > b in the social preference list. Illustration Suppose the set of candidates is {,, }, the set of voters is {P,Q,R} and their preference lists are: P : > >, Q : > >, R : > >. Note that in each individual preference, >. Pareto condition then says that we would have > in the social preference list.
36 Four Desirable riteria Independence of Irrelevant andidates (II) The relative position between candidate and in the social preference list does not depends on the positions of other candidates in the individual preference lists. [ If is preferable to when is absent, then is still preferable to when is present.]
37 Independence of Irrelevant andidates (II) Illustration O = [ P : >, Q : >, R : >]. Suppose we insert another candidate into the above sequence and obtain the following two sequences M and N of individual preference lists. M = [ P : > >, Q : > >, R : > >]. N = [ P : > >, Q : > >, R : > > ]. II says that the relative position of and in the social preference list should be the same as that of O in these two cases.
38 Four Desirable riteria Monotonicity ny individual should not be able to hurt an candidate by ranking it higher. [If the society prefers X to Y, and an individual who once prefers Y to X now places X higher than Y, then the society should still prefer X to Y.]
39 Illustration Monotonicity ny individual should not be able to hurt an candidate by ranking it higher. Suppose we have two sequences of individual preference lists. M = [P : > >, Q : > >, R : > >]. N = [P : > >, Q : > >, R : > > ]. The two sequences M and N are the same except Q raises 's ranking in sequence N. Monotonicity then says that the ranking of in the social preference list produced by sequence N should not be lower than that produced by sequence M.
40 Dictating Set Definition Suppose X is a subset of the set of voters, and and are two distinct candidates. We say X can force > if > in every individual preference list of X implies > in the social preference list. Definition set X is a dictating set if for any distinct candidates and, X can force >.
41 Dictator Exercise: Show that if X is the set of all individuals, then X is a dictating set if the voting procedure satisfies Pareto condition. Definition If p is one of the individuals and X is the set consisting of p alone, then p is called a dictator. Nondictatorship No individual can be a dictator.
42 Some idea why rrow's Impossibility Theorem is true Paul: > > ; Mary: > > ; Jack: > > In this example, everybody agrees >, so by Pareto ondition, > in the social preference list. Then there are three choices of possible of social preference list, namely case i) >> case ii) >> case iii) >>
43 Some idea why rrow's Impossibility Theorem is true Paul: > > ; Mary: > > ; Jack: > > Suppose the social preference list is > > (i.e. case i). In this case we claim that Paul is indeed the dictator.
44 Given that the social preference list for the sequence Paul: > > ; Mary: > > ; Jack: > > is > >. We first show that for each of the following four sequences of preference list, the social preference list is still > >. Paul: > > ; Mary: > > ; Jack: > > Paul: > > ; Mary: > > ; Jack: > > Paul: > > ; Mary: > > ; Jack: > > Paul: > > ; Mary: > > ; Jack: > >
45 Original sequence O=[Paul: > > ; Mary: > > ; Jack: > > ] onsider the first sequence: M=[Paul: > > ; Mary: > > ; Jack: > > ] learly, by Pareto condition, we have > in the social preference list of M. Take away, then the two sequences O and M become the sequence N=[Paul: > ; Mary: > ; Jack: > ]. ccording to II, the relative position of and in the social preference list of N, M and O should be the same. Since in the social preference list of O, we have >, we also have > in the social preference list of M. Therefore, the social preference list of M is still > >.
46 M=[Paul: > > ; Mary: > > ; Jack: > > ] The social preference list of M is > >. onsider the second sequence P=[Paul: > > ; Mary: > > ; Jack: > > ] learly, by Pareto condition, we have > in the social preference list of P. omparing P with M, by Monotonicity, we can conclude that the social preference list of P is still > >.
47 Similarly, by Monotonicity, we can show that for the last two of the following four sequences of preference list, the social preference is still > >. Paul: > > ; Mary: > > ; Jack: > > Paul: > > ; Mary: > > ; Jack: > > Paul: > > ; Mary: > > ; Jack: > > Paul: > > ; Mary: > > ; Jack: > >
48 Given that the social preference list for the sequence O=[Paul: > > ; Mary: > > ; Jack: > > ] is >>. We have proven that for each of the following four sequences of preference list, the social preference list is still > >. Paul: > > ; Mary: > > ; Jack: > > Paul: > > ; Mary: > > ; Jack: > > Paul: > > ; Mary: > > ; Jack: > > Paul: > > ; Mary: > > ; Jack: > >
49 Removing and consider the following four sequences Paul: > ; Mary: > ; Jack: > Paul: > ; Mary: > ; Jack: > Paul: > ; Mary: > ; Jack: > Paul: > ; Mary: > ; Jack: > Then each of them has a social preference list equal to >. This is because if we have > instead, then when we add back to obtain the previous four sequences, by Independent of Irrelevant andidates (II), we will have > in their social preference list which is a contraction.
50 rrow's Impossibility Theorem Paul: > ; Mary: > ; Jack: > Paul: > ; Mary: > ; Jack: > Paul: > ; Mary: > ; Jack: > Paul: > ; Mary: > ; Jack: > We find that > in the society preference list as soon as Paul prefers to! onclusion: Paul is the dictator in the society!!!
51 Reference lan D. Taylor, Mathematics and Politics: Strategy, Voting, Power and Proof, (1995) Springer-Verlag. Jonathan K. Hodge, The Mathematics of Voting and Elections: Hands-On pproach, (2005), merican Mathematical Society. Donald G. Saari, haotic elections! : a mathematician looks at voting, merican Mathematical Society, Donald G. Saari, Hidden Mathematical Structures of Voting, Mathematics and Democracy, Springer erlin, Kenneth J. rrow, Social choice and individual values, (1951, first edition, 1963 second edition), New York,Wiley.
52 rrow's Impossibility Theorem Theorem (rrow, 1950) ny social choice procedure for more than two candidates satisfying the Pareto condition, independence of irrelevant candidates, and monotonicity is a dictatorship. Note that rrow s theorem doesn t say that a dictatorship procedure will satisfy the Pareto condition, independence of irrelevant candidates, and monotonicity. We shall see later that it is indeed the case.
53 rrow's Impossibility Theorem Proposition: The dictatorship procedure satisfies the Pareto condition. Proof. If everyone prefers to, then, in particular, the dictator does. Therefore, > in the social preference list.
54 Exercises: i) Show that the dictatorship procedure satisfies the independence of irrelevant candidates, and monotonicity. ii) Determine if the sequential pair-wise voting with a fixed agenda satisfies the independence of irrelevant candidates. Explain your answer carefully.
55 Strategies in voting Suppose we have three voters,, and two candidates O and N. The preference lists of, and are recorded below. hoice Voter 1 st hoice N N O 2 nd hoice O O N learly s choice O will not be the social choice if we use Simple majority vote.
56 learly s choice O will not be the social choice. However, can then propose a new candidate M in so that we have the following preference lists hoice Voter 1 st hoice M N O 2 nd hoice N O M 3 rd hoice O M N
57 If we use the sequential pair-wise voting with the agenda [M, N, O], then O will be the social choice!. 1 st round nd round N 1 M 2 N O M O
58 Yes-No Voting In a yes-no voting system, each voter either responded with a vote of yes or no. The system also specifies exactly which collections of yes votes yield passage of the motion at hand.
59 Yes-No Voting In a yes-no voting system, any collection of voters is called a coalition. coalition is said to be winning if passage is guaranteed by yea votes from exactly the voters in that coalition. oalitions that are not winning are called losing. Every yes-no voting system can be described by simply listing the winning coalitions. onversely, any collection of subsets of voters gives us a yes-no voting system, although most of the systems arrived at in this way would be of little interest.
60 Examples of Yes-No Voting System United Nations Security ouncil The United Federal System The System to mend the anadian onstitution The Legislative ouncil of HKSR (LEGO)
61 The United Nations Security ouncil The voters in this system are the fifteen countries that make up the security ouncil, five of which (hina, England, France, Russia, and the United States) are called permanent members whereas the other ten are called nonpermanent members. Passage requires a total of at least nine of the fifteen possible votes, subject to a veto due to a nay vote from anyone of the five permanent members. Remark. For simplicity, we ignore the possibility of abstentions in the following discussions.
62 The United States Federal System There are 537 voters in this yes-no voting system: 435 members of the House of Representatives, 100 members of the Senate, the vice president, and the president. The vice president plays the role of tiebreaker in the Senate, and the president has veto power that can be overridden by a two-thirds vote of both the House and the Senate.
63 Thus, for a bill to pass it must be supported by either: or more representatives and 51 or more senators (with or without the vice president) and the president or more representatives and 50 senators and the vice president and the president or more representatives and 67 or more senators (with or without either the vice president or the president).
64 The System to mend the anadian onstitution Since 1982, an amendment to the anadian onstitution becomes law only if it is approved by at least seven of the ten anadian provinces subject to the proviso that the approving provinces have, among them, at least half of anada s population. For our purposes, it will suffice to work with the following population percentages (taken from the 1961census) for the ten anadian provinces:
65 Prince Edward Island (l%) Newfoundland (3%) New runswick (3%) Nova Scotia (4%) Manitoba (5%) Saskatchewan (5%) lberta (7%) ritish olumbia (9%) Quebec (29%) Ontario (34%)
66 LEGO In LEGO, the 60 Members are divided into two groups: 30 Members returned by geographical constituencies through direct elections, and 30 Members by functional constituencies. bill will pass if (a) the bill is proposed by the government and it is supported by more than 30 members, or (b) the bill is proposed by a LEGO member and it is supported by more then 15 members from each group.
67 LEGO In order to transform it into a usual yes-no voting system, we introduce a virtual member who supports a bill if and only if it is proposed by the government. In other world, it is an invisible government representative in LEGO. The 30 members by geographical constituencies are numbered 1,...,30, the 30 members by functional constituencies are numbered 31,,60 and the virtual member is numbered 61.
68 Yes-No Voting Every yes-no voting system can be described by simply listing the winning coalitions. Therefore, a yes-no voting system of n persons is a set V of subsets of {1,,n}. Each element of V is called a winning coalition. We shall identify a subset S of {1,...,n} with the vector (s_1,,s_n) with s_i=1 if i is inside S and s_i=0 if i is not in S.
69 LEGO subset S is a winning coalition if (a) 61 in S and S {1,,60} 31, or (b) 61 is outside S, S {1,,30} 16 and S {16,,60} 16.
70 Weighted system yes-no voting system is said to be a weighted system if it can be described by specifying real number weights for the voters and a real number quota---with no provisos or mention of veto power---such that a coalition is winning precisely when the sum of the weights of the voters in the coalition meets or exceeds the quota.
71 Example. The U.N. Security ouncil is a weighted system. Proof. ssign weight 7 to each permanent member and weight 1 to each nonpermanent member. Let the quota be 39. We must now show that each winning coalition in the U.N. Security ouncil has weight at least 39, and that each losing coalition has weight at most 38.
72 winning coalition in the U.N. Security ouncil must contain all five permanent members (a total weight of 35) and at least four nonpermanent members (an additional weight of 4). Hence, any winning coalition meets or exceeds the quota of 39. losing coalition, on the other hand, either omits a permanent member, and thus has weight at most ( 7 4) + (1 10) = = 38
73 or contains at most three nonpermanent members, and thus has weight at most ( 7 5) + (1 3) = = 38. Hence, any losing coalition falls short of the quota of 39. This completes the proof. Question: Is every yes-no voting system a weighted system?
74 Trade Robust System yes-no voting system is said to be trade robust if an arbitrary exchange of voters among several winning coalitions leaves at least one of the coalitions winning. Referring to the LEGO example, suppose there are 2 winning coalitions X and Y, where X consists of 31 LEGO members and Y consists of 32 LEGO. members. If 3 unique voters in X are exchanged with 10 unique voters in Y, resulting in 38 voters in X and 25 voters in Y. Then X is still a winning coalition.
75 Weighted Vs Trade Robust Theorem. yes-no voting system is weighted if and only if it is trade robust. Remark. The System to mend the anadian onstitution is not trade robust and therefore it is not weighted.
76 The System to mend the anadian onstitution is not trade Robust X: Prince Edward Island (l%), Newfoundland (3%), Manitoba (5%),Saskatchewan (5%),lberta (7%),ritish olumbia (9%),Quebec (29%) Y: New runswick (3%),Nova Scotia (4%), Manitoba (5%), Saskatchewan (5%) lberta (7%),ritish olumbia (9%),Ontario (34%) Now let X and Y be obtained by trading Prince Edward Island and Newfoundland for Ontario. Then X is a losing coalition because is has too few provinces, while Y is also losing as it represents less than half of anada s population.
77 PROPOSITION. Suppose V is a yes-no voting system for the set X of voters, and let m be the number of losing coalitions in V. Then it is possible to find m weighted voting systems with the same set X of voters such that a coalition is winning in V if and only if it is winning in every one of these m weighted systems. Thus, the set of winning coalitions in V is the intersection of the sets of winning coalitions from these m weighted voting systems.
78 Since we have a proposition that guarantees every yes-no voting system can be represented as the intersection of weighted systems, it is natural to ask how efficiently this can be done for a given system. This leads to the following definition. DEFINITION. yes-no voting system is said to be of dimension k if and only if it can be represented as the intersection of exactly k weighted voting systems, but not as the intersection of k - 1 weighted voting systems.
79 Notice that a yes-no voting system is of dimension 1 if and only if it is weighted. We have already proved that the procedure to amend the anadian constitution is of dimension at least 2. One can actually prove that the dimension is equal to 2. Moreover, we also have PROPOSITION. The U.S. federal system has dimension 2.
80 Dimension of a voting system It turns out that for each positive integer k, there is a voting system of dimension k. However in the end of Section 8.3 of lan Taylor s book Mathematics and Politics, it is stated that ``we know of no real-world voting system of dimension 3''. It was proven recently by my colleague Wai Shun heung that the LEGO voting system is of dimension 3.
81 How to measure political power? It is well-known that the number of parliamentary seats for a party in a multiparty system is an inaccurate measure for the effective voting strength of that party. To illustrate this point in a simple way, consider an imaginary parliament consisting of three parties a, b and c each having, respectively, 74, 2 and 74 seats. t first sight, parties a and c, each with 74 seats, seem to be far more powerful than party b with only two seats. However, this is not the case.
82 How to measure political power? Suppose that the absolute majority rule is in use so that to forma majority coalition, at least 76 seats are necessary. The majority coalitions then are {a, b}, {a, c}, {b, c} and {a, b, c}, and we see that party b is in as many winning coalitions as the two other parties. Moreover, it can make as many coalitions losing or winning as the other parties. This strongly indicates that party b is not inferior to the other parties in terms of voting strength.
83 How to measure political power? Hard to be quantified. Does not exist a universal way to calculate political power. So, different ideas lead to different power indices: a) Shapley-Shubik Index of Power (SSI) [1954] b) anzhaf Index of Power (I) [1979] c) Deegan-Packel Index of Power (DPI) [1978]
84 Shapley-Shubik Index of Power (SSI) The pivotal player is the one whose joining converts the growing coalition from a losing one to a winning one ( p) SSI = the number of orderings of X for which p is pivotal the total number of possible orderings of the set X
85 Shapley-Shubik Index of Power (SSI) My colleague Wai Shun heung has tried to quantify the power of the government within LEGO by considering the most common power index, the Shapley-Shubik Index.
86
87
88
89 anzhaf Index of Power (I) TP(p), is the number of coalitions where: 1. p is a member of. 2. is a winning coalition. 3. If p is deleted from, the resulting coalition is not a winning one. I(p 1 ) = TP( p 1 TP( p 1 ) ) TP( p n )
90 Deegan-Packel Index of Power 1, 2, j the minimal winning coalitions in a yes-no voting system V to which a voter (1 voter) or a bloc (p voters), say x, belongs. Take n 1 (no. of voters) in 1, n 2 2, n j j TDPP(x) = p n k DPI (x i ) = TDPP( x TDPP( x i ) ) TDPP( x 1 n )
91 Deegan-Packel Index of Power This index was introduced in 1978 by Deegan and Packel. They designed this based on 3 assumptions: i) only minimal winning coalitions should be considered. ii) all minimal winning coalitions form with equal probability. iii) the amount of power a player derives from belonging to some minimal winning coalition is the same as that derived by any other player belonging to that same minimal winning coalition.
92 The Legislative ouncil in Hong Kong ( ) Political Parties: Liberal Party (8,2) Democratic lliance for the etterment of Hong Kong (D) (2,8) Democratic Party (2,7) ivic Party (3,3) Hong Kong Federation of Trade Unions (FTU) (2,1) Hong Kong onfederation of Trade Unions (HKTU) (0,2) 20 Individuals (13, 7)
93 power indices of different parties in the HKL In general, a bigger bloc has a larger power. 2. Different concepts yield different result SSI I DPI LP D DP P HKFTU HKTU Ind.
94 When comes to the non-weighted part Power indices of parties in HKL (2) 3.Though both has 10 voters, power are not the same DP LP D P 4. ut DPI, HKTU has a slightly higher power than HKFTU! HKFTU HKTU F (Ind.) G (Ind.) SSI DPI
95 onclusion From this as well as the other studies, it is known that one can distinguish two classes of power indices. The first class contains the Shapley-Shubik, the normalized anzhaf and the Penrose-anzhaf index while the second contains the Deegan- Packel and the Holler index.
96 Reference: lan D. Taylor, Mathematics and Politics. Springer-Verlag New York, Inc., Wai Shun heung, Three-Dimensional Voting System in Hong Kong, 2009 (preprint). drian van Deemen1 and gnieszka Rusinowska, Paradoxes of Voting Power in Dutch Politics, Public choice, Volume 115, Numbers 1-2, Legislative ouncil: Thank You!
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
Social Choice: The Impossible Dream. Check off these skills when you feel that you have mastered them.
 Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
Voting Definitions and Theorems Spring Dr. Martin Montgomery Office: POT 761
 Voting Definitions and Theorems Spring 2014 Dr. Martin Montgomery Office: POT 761 http://www.ms.uky.edu/~martinm/m111 Voting Method: Plurality Definition (The Plurality Method of Voting) For each ballot,
Voting Definitions and Theorems Spring 2014 Dr. Martin Montgomery Office: POT 761 http://www.ms.uky.edu/~martinm/m111 Voting Method: Plurality Definition (The Plurality Method of Voting) For each ballot,
The Manipulability of Voting Systems. Check off these skills when you feel that you have mastered them.
 Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
9.3 Other Voting Systems for Three or More Candidates
 9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
Elections with Only 2 Alternatives
 Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Mathematical Thinking. Chapter 9 Voting Systems
 Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Mathematics and Social Choice Theory. Topic 4 Voting methods with more than 2 alternatives. 4.1 Social choice procedures
 Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
The mathematics of voting, power, and sharing Part 1
 The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
Arrow s Impossibility Theorem
 Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
Fairness Criteria. Review: Election Methods
 Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory
 MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
Notes for Session 7 Basic Voting Theory and Arrow s Theorem
 Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Fairness Criteria. Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election.
 Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
The Mathematics of Elections
 MTH 110 Week 1 hapter 1 Worksheet NME The Mathematics of Elections It s not the voting that s democracy; it s the counting. Tom Stoppard We have elections because we don t all think alike. Since we cannot
MTH 110 Week 1 hapter 1 Worksheet NME The Mathematics of Elections It s not the voting that s democracy; it s the counting. Tom Stoppard We have elections because we don t all think alike. Since we cannot
1.6 Arrow s Impossibility Theorem
 1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
Voting: Issues, Problems, and Systems, Continued
 Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
This situation where each voter is not equal in the number of votes they control is called:
 Finite Mathematics Notes Chapter 2: The Mathematics of Power (Weighted Voting) Academic Standards: PS.ED.2: Use election theory techniques to analyze election data. Use weighted voting techniques to decide
Finite Mathematics Notes Chapter 2: The Mathematics of Power (Weighted Voting) Academic Standards: PS.ED.2: Use election theory techniques to analyze election data. Use weighted voting techniques to decide
Desirable properties of social choice procedures. We now outline a number of properties that are desirable for these social choice procedures:
 Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Voting Criteria April
 Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
This situation where each voter is not equal in the number of votes they control is called:
 Finite Math A Chapter 2, Weighted Voting Systems 1 Discrete Mathematics Notes Chapter 2: Weighted Voting Systems The Power Game Academic Standards: PS.ED.2: Use election theory techniques to analyze election
Finite Math A Chapter 2, Weighted Voting Systems 1 Discrete Mathematics Notes Chapter 2: Weighted Voting Systems The Power Game Academic Standards: PS.ED.2: Use election theory techniques to analyze election
Chapter 10. The Manipulability of Voting Systems. For All Practical Purposes: Effective Teaching. Chapter Briefing
 Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
Warm Up Day 2 Determine the Plurality, Borda, Runoff, and Sequential Runoff winners.
 Warm Up Day 2 Determine the Plurality, orda, Runoff, and Sequential Runoff winners. D D D D 10 4 7 8 HW Questions? Pairwise Voting Once all of the ballots are submitted, we consider all of the different
Warm Up Day 2 Determine the Plurality, orda, Runoff, and Sequential Runoff winners. D D D D 10 4 7 8 HW Questions? Pairwise Voting Once all of the ballots are submitted, we consider all of the different
French. Chinese. Mexican. Italian
 Lesson 1. rrow s onditions and pproval Voting Paradoxes, unfair results, and insincere voting are some of the problems that have caused people to look for better models for reaching group decisions. In
Lesson 1. rrow s onditions and pproval Voting Paradoxes, unfair results, and insincere voting are some of the problems that have caused people to look for better models for reaching group decisions. In
Check off these skills when you feel that you have mastered them. Identify if a dictator exists in a given weighted voting system.
 Chapter Objectives Check off these skills when you feel that you have mastered them. Interpret the symbolic notation for a weighted voting system by identifying the quota, number of voters, and the number
Chapter Objectives Check off these skills when you feel that you have mastered them. Interpret the symbolic notation for a weighted voting system by identifying the quota, number of voters, and the number
The Mathematics of Voting
 Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
How should we count the votes?
 How should we count the votes? Bruce P. Conrad January 16, 2008 Were the Iowa caucuses undemocratic? Many politicians, pundits, and reporters thought so in the weeks leading up to the January 3, 2008 event.
How should we count the votes? Bruce P. Conrad January 16, 2008 Were the Iowa caucuses undemocratic? Many politicians, pundits, and reporters thought so in the weeks leading up to the January 3, 2008 event.
Homework 4 solutions
 Homework 4 solutions ASSIGNMENT: exercises 2, 3, 4, 8, and 17 in Chapter 2, (pp. 65 68). Solution to Exercise 2. A coalition that has exactly 12 votes is winning because it meets the quota. This coalition
Homework 4 solutions ASSIGNMENT: exercises 2, 3, 4, 8, and 17 in Chapter 2, (pp. 65 68). Solution to Exercise 2. A coalition that has exactly 12 votes is winning because it meets the quota. This coalition
Social welfare functions
 Social welfare functions We have defined a social choice function as a procedure that determines for each possible profile (set of preference ballots) of the voters the winner or set of winners for the
Social welfare functions We have defined a social choice function as a procedure that determines for each possible profile (set of preference ballots) of the voters the winner or set of winners for the
SOCIAL CHOICES (Voting Methods) THE PROBLEM. Social Choice and Voting. Terminologies
 SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
(67686) Mathematical Foundations of AI June 18, Lecture 6
 (67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
(67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
Warm Up Day 2. # Problem Work Answer 1 2
 Get out a NEW sheet of Notebook Paper for the warm-up. Title it Unit 6 Warm-Ups N put your name on it! Set up your warm-up paper like the orrections format # Problem Work nswer 1 2 Warm Up ay 2 Go to this
Get out a NEW sheet of Notebook Paper for the warm-up. Title it Unit 6 Warm-Ups N put your name on it! Set up your warm-up paper like the orrections format # Problem Work nswer 1 2 Warm Up ay 2 Go to this
answers to some of the sample exercises : Public Choice
 answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
Exercises For DATA AND DECISIONS. Part I Voting
 Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Chapter 11. Weighted Voting Systems. For All Practical Purposes: Effective Teaching
 Chapter Weighted Voting Systems For All Practical Purposes: Effective Teaching In observing other faculty or TA s, if you discover a teaching technique that you feel was particularly effective, don t hesitate
Chapter Weighted Voting Systems For All Practical Purposes: Effective Teaching In observing other faculty or TA s, if you discover a teaching technique that you feel was particularly effective, don t hesitate
Chapter 1 Review. 1. Write a summary of what you think are the important points of this chapter. 2. Consider the following set of preferences.
 hapter 1 Review 1. Write a summary of what you think are the important points of this chapter. 2. onsider the following set of preferences. E E E E 20 22 12 9 a. etermine a winner using a 5-4-3-2-1 orda
hapter 1 Review 1. Write a summary of what you think are the important points of this chapter. 2. onsider the following set of preferences. E E E E 20 22 12 9 a. etermine a winner using a 5-4-3-2-1 orda
Chapter 9: Social Choice: The Impossible Dream
 Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
2-Candidate Voting Method: Majority Rule
 2-Candidate Voting Method: Majority Rule Definition (2-Candidate Voting Method: Majority Rule) Majority Rule is a form of 2-candidate voting in which the candidate who receives the most votes is the winner
2-Candidate Voting Method: Majority Rule Definition (2-Candidate Voting Method: Majority Rule) Majority Rule is a form of 2-candidate voting in which the candidate who receives the most votes is the winner
Computational Social Choice: Spring 2007
 Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
The Mathematics of Voting. The Mathematics of Voting
 1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
Voting rules: (Dixit and Skeath, ch 14) Recall parkland provision decision:
 rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
Introduction to the Theory of Voting
 November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
Rock the Vote or Vote The Rock
 Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
VOTING SYSTEMS AND ARROW S THEOREM
 VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Voting Criteria: Majority Criterion Condorcet Criterion Monotonicity Criterion Independence of Irrelevant Alternatives Criterion
 We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
Rationality of Voting and Voting Systems: Lecture II
 Rationality of Voting and Voting Systems: Lecture II Rationality of Voting Systems Hannu Nurmi Department of Political Science University of Turku Three Lectures at National Research University Higher
Rationality of Voting and Voting Systems: Lecture II Rationality of Voting Systems Hannu Nurmi Department of Political Science University of Turku Three Lectures at National Research University Higher
Voting. Suppose that the outcome is determined by the mean of all voter s positions.
 Voting Suppose that the voters are voting on a single-dimensional issue. (Say 0 is extreme left and 100 is extreme right for example.) Each voter has a favorite point on the spectrum and the closer the
Voting Suppose that the voters are voting on a single-dimensional issue. (Say 0 is extreme left and 100 is extreme right for example.) Each voter has a favorite point on the spectrum and the closer the
Lecture 7 A Special Class of TU games: Voting Games
 Lecture 7 A Special Class of TU games: Voting Games The formation of coalitions is usual in parliaments or assemblies. It is therefore interesting to consider a particular class of coalitional games that
Lecture 7 A Special Class of TU games: Voting Games The formation of coalitions is usual in parliaments or assemblies. It is therefore interesting to consider a particular class of coalitional games that
Lesson 1.3. More Group-Ranking Models and Paradoxes
 M01_Final.qxp:M01.qxp 5/9/14 1:54 PM Page 18 Lesson 1.3 More Group-Ranking Models and Paradoxes ifferent models for finding a group ranking can give different results. This fact led the Marquis de ondorcet
M01_Final.qxp:M01.qxp 5/9/14 1:54 PM Page 18 Lesson 1.3 More Group-Ranking Models and Paradoxes ifferent models for finding a group ranking can give different results. This fact led the Marquis de ondorcet
Social Choice Theory. Denis Bouyssou CNRS LAMSADE
 A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
Arrow s Impossibility Theorem on Social Choice Systems
 Arrow s Impossibility Theorem on Social Choice Systems Ashvin A. Swaminathan January 11, 2013 Abstract Social choice theory is a field that concerns methods of aggregating individual interests to determine
Arrow s Impossibility Theorem on Social Choice Systems Ashvin A. Swaminathan January 11, 2013 Abstract Social choice theory is a field that concerns methods of aggregating individual interests to determine
Borda s Paradox. Theodoros Levantakis
 orda s Paradox Theodoros Levantakis Jean-harles de orda Jean-harles hevalier de orda (May 4, 1733 February 19, 1799), was a French mathematician, physicist, political scientist, and sailor. In 1770, orda
orda s Paradox Theodoros Levantakis Jean-harles de orda Jean-harles hevalier de orda (May 4, 1733 February 19, 1799), was a French mathematician, physicist, political scientist, and sailor. In 1770, orda
Chapter 4: Voting and Social Choice.
 Chapter 4: Voting and Social Choice. Topics: Ordinal Welfarism Condorcet and Borda: 2 alternatives for majority voting Voting over Resource Allocation Single-Peaked Preferences Intermediate Preferences
Chapter 4: Voting and Social Choice. Topics: Ordinal Welfarism Condorcet and Borda: 2 alternatives for majority voting Voting over Resource Allocation Single-Peaked Preferences Intermediate Preferences
Social choice theory
 Social choice theory A brief introduction Denis Bouyssou CNRS LAMSADE Paris, France Introduction Motivation Aims analyze a number of properties of electoral systems present a few elements of the classical
Social choice theory A brief introduction Denis Bouyssou CNRS LAMSADE Paris, France Introduction Motivation Aims analyze a number of properties of electoral systems present a few elements of the classical
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
Voting Lecture 3: 2-Candidate Voting Spring Morgan Schreffler Office: POT Teaching.
 Voting Lecture 3: 2-Candidate Voting Spring 2014 Morgan Schreffler Office: POT 902 http://www.ms.uky.edu/~mschreffler/ Teaching.php 2-Candidate Voting Method: Majority Rule Definition (2-Candidate Voting
Voting Lecture 3: 2-Candidate Voting Spring 2014 Morgan Schreffler Office: POT 902 http://www.ms.uky.edu/~mschreffler/ Teaching.php 2-Candidate Voting Method: Majority Rule Definition (2-Candidate Voting
CS 886: Multiagent Systems. Fall 2016 Kate Larson
 CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
Grab a Unit 6 Election Theory Packet! Write down tonight s HW: Packet p. 1-3
 Grab a Unit 6 Election Theory Packet! Write down tonight s HW: Packet p. 1-3 Homecoming King and Queen Elections You have been chosen to serve on the committee that decides who this year's Homecoming King
Grab a Unit 6 Election Theory Packet! Write down tonight s HW: Packet p. 1-3 Homecoming King and Queen Elections You have been chosen to serve on the committee that decides who this year's Homecoming King
Many Social Choice Rules
 Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
Introduction to Theory of Voting. Chapter 2 of Computational Social Choice by William Zwicker
 Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Voting: Issues, Problems, and Systems, Continued. Voting II 1/27
 Voting: Issues, Problems, and Systems, Continued Voting II 1/27 Last Time Last time we discussed some elections and some issues with plurality voting. We started to discuss another voting system, the Borda
Voting: Issues, Problems, and Systems, Continued Voting II 1/27 Last Time Last time we discussed some elections and some issues with plurality voting. We started to discuss another voting system, the Borda
The Mathematics of Power: Weighted Voting
 MATH 110 Week 2 Chapter 2 Worksheet The Mathematics of Power: Weighted Voting NAME The Electoral College offers a classic illustration of weighted voting. The Electoral College consists of 51 voters (the
MATH 110 Week 2 Chapter 2 Worksheet The Mathematics of Power: Weighted Voting NAME The Electoral College offers a classic illustration of weighted voting. The Electoral College consists of 51 voters (the
Problems with Group Decision Making
 Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Public Choice. Slide 1
 Public Choice We investigate how people can come up with a group decision mechanism. Several aspects of our economy can not be handled by the competitive market. Whenever there is market failure, there
Public Choice We investigate how people can come up with a group decision mechanism. Several aspects of our economy can not be handled by the competitive market. Whenever there is market failure, there
Voting Fairness Idea: Condorcet Criterion (CO)
 Voting Fairness Idea: ondorcet riterion (O) Definition (Voting Fairness Idea: ondorcet riterion (O)) voting system satisfies the ondorcet riterion if the ondorcet andidate always wins. In the ballots below,
Voting Fairness Idea: ondorcet riterion (O) Definition (Voting Fairness Idea: ondorcet riterion (O)) voting system satisfies the ondorcet riterion if the ondorcet andidate always wins. In the ballots below,
Election Theory. How voters and parties behave strategically in democratic systems. Mark Crowley
 How voters and parties behave strategically in democratic systems Department of Computer Science University of British Columbia January 30, 2006 Sources Voting Theory Jeff Gill and Jason Gainous. "Why
How voters and parties behave strategically in democratic systems Department of Computer Science University of British Columbia January 30, 2006 Sources Voting Theory Jeff Gill and Jason Gainous. "Why
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections
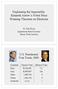 Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Math for Liberal Studies
 Math for Liberal Studies There are many more methods for determining the winner of an election with more than two candidates We will only discuss a few more: sequential pairwise voting contingency voting
Math for Liberal Studies There are many more methods for determining the winner of an election with more than two candidates We will only discuss a few more: sequential pairwise voting contingency voting
Economics 470 Some Notes on Simple Alternatives to Majority Rule
 Economics 470 Some Notes on Simple Alternatives to Majority Rule Some of the voting procedures considered here are not considered as a means of revealing preferences on a public good issue, but as a means
Economics 470 Some Notes on Simple Alternatives to Majority Rule Some of the voting procedures considered here are not considered as a means of revealing preferences on a public good issue, but as a means
Topics on the Border of Economics and Computation December 18, Lecture 8
 Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
Power in Voting Games and Canadian Politics
 Power in Voting Games and Canadian Politics Chris Nicola December 27, 2006 Abstract In this work we examine power measures used in the analysis of voting games to quantify power. We consider both weighted
Power in Voting Games and Canadian Politics Chris Nicola December 27, 2006 Abstract In this work we examine power measures used in the analysis of voting games to quantify power. We consider both weighted
Voting and Markov Processes
 Voting and Markov Processes Andrew Nicholson Department of Mathematics The University of North Carolina at Asheville One University Heights Asheville, NC 884. USA Faculty Advisor: Dr. Sam Kaplan Abstract
Voting and Markov Processes Andrew Nicholson Department of Mathematics The University of North Carolina at Asheville One University Heights Asheville, NC 884. USA Faculty Advisor: Dr. Sam Kaplan Abstract
A Mathematical View on Voting and Power
 A Mathematical View on Voting and Power Werner Kirsch Abstract. In this article we describe some concepts, ideas and results from the mathematical theory of voting. We give a mathematical description of
A Mathematical View on Voting and Power Werner Kirsch Abstract. In this article we describe some concepts, ideas and results from the mathematical theory of voting. We give a mathematical description of
Social Choice & Mechanism Design
 Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
Math for Liberal Arts MAT 110: Chapter 12 Notes
 Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
Algorithms, Games, and Networks February 7, Lecture 8
 Algorithms, Games, and Networks February 7, 2013 Lecturer: Ariel Procaccia Lecture 8 Scribe: Dong Bae Jun 1 Overview In this lecture, we discuss the topic of social choice by exploring voting rules, axioms,
Algorithms, Games, and Networks February 7, 2013 Lecturer: Ariel Procaccia Lecture 8 Scribe: Dong Bae Jun 1 Overview In this lecture, we discuss the topic of social choice by exploring voting rules, axioms,
Recall: Properties of ranking rules. Recall: Properties of ranking rules. Kenneth Arrow. Recall: Properties of ranking rules. Strategically vulnerable
 Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Voting Protocols. Introduction. Social choice: preference aggregation Our settings. Voting protocols are examples of social choice mechanisms
 Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
The Math of Rational Choice - Math 100 Spring 2015
 The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
Today s plan: Section : Plurality with Elimination Method and a second Fairness Criterion: The Monotocity Criterion.
 1 Today s plan: Section 1.2.4. : Plurality with Elimination Method and a second Fairness Criterion: The Monotocity Criterion. 2 Plurality with Elimination is a third voting method. It is more complicated
1 Today s plan: Section 1.2.4. : Plurality with Elimination Method and a second Fairness Criterion: The Monotocity Criterion. 2 Plurality with Elimination is a third voting method. It is more complicated
Voting: Issues, Problems, and Systems. Voting I 1/36
 Voting: Issues, Problems, and Systems Voting I 1/36 Each even year every member of the house is up for election and about a third of the senate seats are up for grabs. Most people do not realize that there
Voting: Issues, Problems, and Systems Voting I 1/36 Each even year every member of the house is up for election and about a third of the senate seats are up for grabs. Most people do not realize that there
Make the Math Club Great Again! The Mathematics of Democratic Voting
 Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
Problems with Group Decision Making
 Problems with Group Decision Making There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Problems with Group Decision Making There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
The Integer Arithmetic of Legislative Dynamics
 The Integer Arithmetic of Legislative Dynamics Kenneth Benoit Trinity College Dublin Michael Laver New York University July 8, 2005 Abstract Every legislature may be defined by a finite integer partition
The Integer Arithmetic of Legislative Dynamics Kenneth Benoit Trinity College Dublin Michael Laver New York University July 8, 2005 Abstract Every legislature may be defined by a finite integer partition
Social Choice. CSC304 Lecture 21 November 28, Allan Borodin Adapted from Craig Boutilier s slides
 Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Chapter 1 Practice Test Questions
 0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
MATH 1340 Mathematics & Politics
 MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
Lecture 12: Topics in Voting Theory
 Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
On Axiomatization of Power Index of Veto
 On Axiomatization of Power Index of Veto Jacek Mercik Wroclaw University of Technology, Wroclaw, Poland jacek.mercik@pwr.wroc.pl Abstract. Relations between all constitutional and government organs must
On Axiomatization of Power Index of Veto Jacek Mercik Wroclaw University of Technology, Wroclaw, Poland jacek.mercik@pwr.wroc.pl Abstract. Relations between all constitutional and government organs must
Rationality & Social Choice. Dougherty, POLS 8000
 Rationality & Social Choice Dougherty, POLS 8000 Social Choice A. Background 1. Social Choice examines how to aggregate individual preferences fairly. a. Voting is an example. b. Think of yourself writing
Rationality & Social Choice Dougherty, POLS 8000 Social Choice A. Background 1. Social Choice examines how to aggregate individual preferences fairly. a. Voting is an example. b. Think of yourself writing
Voting Systems. High School Circle I. June 4, 2017
 Voting Systems High School Circle I June 4, 2017 Today we are going to start our study of voting systems. Put loosely, a voting system takes the preferences of many people, and converted them into a group
Voting Systems High School Circle I June 4, 2017 Today we are going to start our study of voting systems. Put loosely, a voting system takes the preferences of many people, and converted them into a group
Grade 6 Math Circles Winter February 27/28 The Mathematics of Voting - Solutions
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles Winter 2018 - February 27/28 The Mathematics of Voting - Solutions Warm-up: Time
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles Winter 2018 - February 27/28 The Mathematics of Voting - Solutions Warm-up: Time
Measuring Fairness. Paul Koester () MA 111, Voting Theory September 7, / 25
 Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Name Date I. Consider the preference schedule in an election with 5 candidates.
 Name Date I. Consider the preference schedule in an election with 5 candidates. 1. How many voters voted in this election? 2. How many votes are needed for a majority (more than 50% of the vote)? 3. How
Name Date I. Consider the preference schedule in an election with 5 candidates. 1. How many voters voted in this election? 2. How many votes are needed for a majority (more than 50% of the vote)? 3. How
Dealing with Incomplete Agents Preferences and an Uncertain Agenda in Group Decision Making via Sequential Majority Voting
 Proceedings, Eleventh International onference on Principles of Knowledge Representation and Reasoning (2008) Dealing with Incomplete gents Preferences and an Uncertain genda in Group Decision Making via
Proceedings, Eleventh International onference on Principles of Knowledge Representation and Reasoning (2008) Dealing with Incomplete gents Preferences and an Uncertain genda in Group Decision Making via
BOOK REVIEW BY DAVID RAMSEY, UNIVERSITY OF LIMERICK, IRELAND
 B A D A N I A O P E R A C Y J N E I D E C Y Z J E Nr 2 2008 BOOK REVIEW BY DAVID RAMSEY, UNIVERSITY OF LIMERICK, IRELAND Power, Freedom and Voting Essays in honour of Manfred J. Holler Edited by Matthew
B A D A N I A O P E R A C Y J N E I D E C Y Z J E Nr 2 2008 BOOK REVIEW BY DAVID RAMSEY, UNIVERSITY OF LIMERICK, IRELAND Power, Freedom and Voting Essays in honour of Manfred J. Holler Edited by Matthew
In this lecture, we will explore weighted voting systems further. Examples of shortcuts to determining winning coalitions and critical players.
 In this lecture, we will explore weighted voting systems further. Examples of shortcuts to determining winning coalitions and critical players. Determining winning coalitions, critical players, and power
In this lecture, we will explore weighted voting systems further. Examples of shortcuts to determining winning coalitions and critical players. Determining winning coalitions, critical players, and power
Mathematics of Voting Systems. Tanya Leise Mathematics & Statistics Amherst College
 Mathematics of Voting Systems Tanya Leise Mathematics & Statistics Amherst College Arrow s Impossibility Theorem 1) No special treatment of particular voters or candidates 2) Transitivity A>B and B>C implies
Mathematics of Voting Systems Tanya Leise Mathematics & Statistics Amherst College Arrow s Impossibility Theorem 1) No special treatment of particular voters or candidates 2) Transitivity A>B and B>C implies
