Voting rules: (Dixit and Skeath, ch 14) Recall parkland provision decision:
|
|
|
- Gervase Underwood
- 5 years ago
- Views:
Transcription
1 rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = there are two groups of individuals in society: 8 have α=, 1 1 and remaining 2 have α = So: efficient to provide public good, since sum of benefits (40) > total cost (38). Suppose held a referendum on provision; would parkland be provided (with this financing scheme)? Depends.on voting scheme used. Possible schemes? Page 1 of 8
2 General: classifiy vote aggregation methods by number of options or candidates at any time: three types: A. Binary: two alternatives - if only two, aggregate votes by majority rule; - if more than two: sequence of pairwise votes, winner by majority rule; - types? 1. Condorcet method: round robin; overall winner is the one who defeats all others in pairwise contests. 2. successive elimination (various indices) B. Plurative methods: simultaneously consider multiple options 1. plurality rule: - each voter has one vote; - candidate with most votes wins; - plurality may be less than majority Page 2 of 8
3 2. Borda count: - voters rank order all options - assign points to each, based on own ranking - if 3 alternatives, then most preferred gets 3 points, least preferred gets 1 - sum points across voters - highest wins 3. Approval voting: - vote for any, and all, of which approve; - winner(s): highest number of votes C Mixed methods - multistage - combine binary and plurative paradoxes: 1. Condorcet Paradox: intransitivity of social ordering - best known (among economists) - may be no winner - that is, no alternative which is successful against all others: Page 3 of 8
4 Example: suppose three individuals (1,2,3) choosing one of three options (A,B,C); preferences are - Ind'l 1: A B C - Ind'l 2: B C A - Ind'l 3: C A B Results? A wins in (A,B); B wins in (B,C); C wins in (A,C) - social ordering: A B C A 2. Reversal Paradox: - from Borda count: when slate of candidates changes after votes, and new vote held - need at least 4 candidates (A,B,C,D) - Suppose 7 voters A D A B D D B B A B C A A C C B C D B B D D C D A C C A - With all four options, winner is A: A: 2*4 + 3*3 + 2*1=19 B: 2*4 + 2*3 + 3*1=15 C: 2*3 + 2*2 + 3*1=13 D: 3*4 + 2*2 + 2*1=18 Page 4 of 8
5 Now: suppose discovered that C not valid alternative - vote again, with A,B,D on ballot (same voters): A D A B D D B B A B D A A D D B D A B B A Now, winner is D: A: 2*3 + 3*2 + 2*1=14 B: 2*3 + 2*2 + 3*1=13 D: 3*3 + 2*2 + 2*1=15 (eliminated an irrelevant alternative?) 3. Agenda Paradox: - binary elections - winner goes on, loser doesn't - matters who meets whom first. 4. Different methods give different outcomes Example: 100 voters, in 3 distinct groups: 40: A B C 25: B C A 35: C B A Page 5 of 8
6 Who wins election? a) plurality: A b) Borda count: each voter assigns numbers 1,2,3 to candidates - 3 indicating "most preferred" A obtains 40x3 + 60x1 = 180 B " 25x3 + 75x2 = 225 C " 35x3 + 25x2 + 40x1 = 195 Hence B wins. c) Majority run-off: use first round to eliminate one alternative (lowest number of votes); second round pairs top two from first round. Here, C wins. Is there a "best", reasonable voting rule? No. Page 6 of 8
7 Arrow's "impossibility theorem" Six criteria for aggregation of preferences 1. complete ranking 2. transitive ranking 3. Pareto property: unanimous preferences within population reflected in social ranking 4. ranking not independent of preferences of individuals in soc'y 5. ranking not dictatorial - not the reflection of the preferences of one individual 6. independent of irrelevant alternatives Theorem? no such ranking exists. How to choose between flawed mechanisms? One criterion is manipulability - how easy is it to affect outcome by strategic voting - not voting in accord with own preferences, to produce a result which is more in accord with preferences. Page 7 of 8
8 Consider a voting game in which 3 players (denoted 1, 2, and 3) are deciding among three alternatives (A, B, and C). Alternative B is the "status quo" and alternatives A and C are "challengers". In the first stage, players choose which of the two challengers should be considered; they do this by casting votes for either A or C, with the majority choice being the winner and abstentions not allowed. In the second stage, players vote between the status quo (B) and the winner of the first stage, with majority rule again determining the winner. The players care only about the alternative that is finally selected. The payoffs are u ( A) = u ( B) = u ( C) = 2; u ( B) = u ( C) = u ( A) = 0; u ( C) = u ( A) = u ( B) = Suppose that at each stage each player votes for the alternative they most prefer as the final outcome. a) What would the outcome be? Do these strategies constitute a Nash equilibrium? Page 8 of 8
Arrow s Impossibility Theorem
 Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
1.6 Arrow s Impossibility Theorem
 1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
Chapter 1 Practice Test Questions
 0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
Elections with Only 2 Alternatives
 Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
The Impossibilities of Voting
 The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
Notes for Session 7 Basic Voting Theory and Arrow s Theorem
 Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Desirable properties of social choice procedures. We now outline a number of properties that are desirable for these social choice procedures:
 Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Measuring Fairness. Paul Koester () MA 111, Voting Theory September 7, / 25
 Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Voting Criteria: Majority Criterion Condorcet Criterion Monotonicity Criterion Independence of Irrelevant Alternatives Criterion
 We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
12.2 Defects in Voting Methods
 12.2 Defects in Voting Methods Recall the different Voting Methods: 1. Plurality - one vote to one candidate, the others get nothing The remaining three use a preference ballot, where all candidates are
12.2 Defects in Voting Methods Recall the different Voting Methods: 1. Plurality - one vote to one candidate, the others get nothing The remaining three use a preference ballot, where all candidates are
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Fairness Criteria. Review: Election Methods
 Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
answers to some of the sample exercises : Public Choice
 answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
(67686) Mathematical Foundations of AI June 18, Lecture 6
 (67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
(67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
Exercises For DATA AND DECISIONS. Part I Voting
 Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Economics 470 Some Notes on Simple Alternatives to Majority Rule
 Economics 470 Some Notes on Simple Alternatives to Majority Rule Some of the voting procedures considered here are not considered as a means of revealing preferences on a public good issue, but as a means
Economics 470 Some Notes on Simple Alternatives to Majority Rule Some of the voting procedures considered here are not considered as a means of revealing preferences on a public good issue, but as a means
Recall: Properties of ranking rules. Recall: Properties of ranking rules. Kenneth Arrow. Recall: Properties of ranking rules. Strategically vulnerable
 Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
9.3 Other Voting Systems for Three or More Candidates
 9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
Voting. Suppose that the outcome is determined by the mean of all voter s positions.
 Voting Suppose that the voters are voting on a single-dimensional issue. (Say 0 is extreme left and 100 is extreme right for example.) Each voter has a favorite point on the spectrum and the closer the
Voting Suppose that the voters are voting on a single-dimensional issue. (Say 0 is extreme left and 100 is extreme right for example.) Each voter has a favorite point on the spectrum and the closer the
Fairness Criteria. Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election.
 Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Social Choice & Mechanism Design
 Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
POSITIVE POLITICAL THEORY
 POSITIVE POITICA THEORY SOME IMPORTANT THEOREMS AME THEORY IN POITICA SCIENCE Mirror mirror on the wall which is the fairest of them all????? alatasaray Fenerbahce Besiktas Turkcell Telsim Aria DSP DP
POSITIVE POITICA THEORY SOME IMPORTANT THEOREMS AME THEORY IN POITICA SCIENCE Mirror mirror on the wall which is the fairest of them all????? alatasaray Fenerbahce Besiktas Turkcell Telsim Aria DSP DP
Voting: Issues, Problems, and Systems, Continued
 Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
Mathematics and Social Choice Theory. Topic 4 Voting methods with more than 2 alternatives. 4.1 Social choice procedures
 Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Name Date I. Consider the preference schedule in an election with 5 candidates.
 Name Date I. Consider the preference schedule in an election with 5 candidates. 1. How many voters voted in this election? 2. How many votes are needed for a majority (more than 50% of the vote)? 3. How
Name Date I. Consider the preference schedule in an election with 5 candidates. 1. How many voters voted in this election? 2. How many votes are needed for a majority (more than 50% of the vote)? 3. How
The Mathematics of Voting. The Mathematics of Voting
 1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate.
 Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
Lecture 16: Voting systems
 Lecture 16: Voting systems Economics 336 Economics 336 (Toronto) Lecture 16: Voting systems 1 / 18 Introduction Last lecture we looked at the basic theory of majority voting: instability in voting: Condorcet
Lecture 16: Voting systems Economics 336 Economics 336 (Toronto) Lecture 16: Voting systems 1 / 18 Introduction Last lecture we looked at the basic theory of majority voting: instability in voting: Condorcet
Voting Methods
 1.3-1.5 Voting Methods Some announcements Homework #1: Text (pages 28-33) 1, 4, 7, 10, 12, 19, 22, 29, 32, 38, 42, 50, 51, 56-60, 61, 65 (this is posted on Sakai) Math Center study sessions with Katie
1.3-1.5 Voting Methods Some announcements Homework #1: Text (pages 28-33) 1, 4, 7, 10, 12, 19, 22, 29, 32, 38, 42, 50, 51, 56-60, 61, 65 (this is posted on Sakai) Math Center study sessions with Katie
Head-to-Head Winner. To decide if a Head-to-Head winner exists: Every candidate is matched on a one-on-one basis with every other candidate.
 Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
Public Choice. Slide 1
 Public Choice We investigate how people can come up with a group decision mechanism. Several aspects of our economy can not be handled by the competitive market. Whenever there is market failure, there
Public Choice We investigate how people can come up with a group decision mechanism. Several aspects of our economy can not be handled by the competitive market. Whenever there is market failure, there
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory
 MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
Social Choice: The Impossible Dream. Check off these skills when you feel that you have mastered them.
 Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
Mathematical Thinking. Chapter 9 Voting Systems
 Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Math for Liberal Studies
 Math for Liberal Studies As we have discussed, when there are only two candidates in an election, deciding the winner is easy May s Theorem states that majority rule is the best system However, the situation
Math for Liberal Studies As we have discussed, when there are only two candidates in an election, deciding the winner is easy May s Theorem states that majority rule is the best system However, the situation
Chapter 10. The Manipulability of Voting Systems. For All Practical Purposes: Effective Teaching. Chapter Briefing
 Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
Main idea: Voting systems matter.
 Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
Computational Social Choice: Spring 2007
 Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
SOCIAL CHOICES (Voting Methods) THE PROBLEM. Social Choice and Voting. Terminologies
 SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections
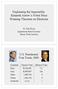 Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Voting: Issues, Problems, and Systems, Continued. Voting II 1/27
 Voting: Issues, Problems, and Systems, Continued Voting II 1/27 Last Time Last time we discussed some elections and some issues with plurality voting. We started to discuss another voting system, the Borda
Voting: Issues, Problems, and Systems, Continued Voting II 1/27 Last Time Last time we discussed some elections and some issues with plurality voting. We started to discuss another voting system, the Borda
Make the Math Club Great Again! The Mathematics of Democratic Voting
 Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
Voting Criteria April
 Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
Social welfare functions
 Social welfare functions We have defined a social choice function as a procedure that determines for each possible profile (set of preference ballots) of the voters the winner or set of winners for the
Social welfare functions We have defined a social choice function as a procedure that determines for each possible profile (set of preference ballots) of the voters the winner or set of winners for the
Chapter 4: Voting and Social Choice.
 Chapter 4: Voting and Social Choice. Topics: Ordinal Welfarism Condorcet and Borda: 2 alternatives for majority voting Voting over Resource Allocation Single-Peaked Preferences Intermediate Preferences
Chapter 4: Voting and Social Choice. Topics: Ordinal Welfarism Condorcet and Borda: 2 alternatives for majority voting Voting over Resource Allocation Single-Peaked Preferences Intermediate Preferences
Topics on the Border of Economics and Computation December 18, Lecture 8
 Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
Social Choice. CSC304 Lecture 21 November 28, Allan Borodin Adapted from Craig Boutilier s slides
 Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
The Manipulability of Voting Systems. Check off these skills when you feel that you have mastered them.
 Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
Homework 7 Answers PS 30 November 2013
 Homework 7 Answers PS 30 November 2013 1. Say that there are three people and five candidates {a, b, c, d, e}. Say person 1 s order of preference (from best to worst) is c, b, e, d, a. Person 2 s order
Homework 7 Answers PS 30 November 2013 1. Say that there are three people and five candidates {a, b, c, d, e}. Say person 1 s order of preference (from best to worst) is c, b, e, d, a. Person 2 s order
The Mathematics of Voting
 The Mathematics of Voting Voting Methods Summary Last time, we considered elections for Math Club President from among four candidates: Alisha (A), Boris (B), Carmen (C), and Dave (D). All 37 voters submitted
The Mathematics of Voting Voting Methods Summary Last time, we considered elections for Math Club President from among four candidates: Alisha (A), Boris (B), Carmen (C), and Dave (D). All 37 voters submitted
Introduction to Social Choice
 for to Social Choice University of Waterloo January 14, 2013 Outline for 1 2 3 4 for 5 What Is Social Choice Theory for Study of decision problems in which a group has to make the decision The decision
for to Social Choice University of Waterloo January 14, 2013 Outline for 1 2 3 4 for 5 What Is Social Choice Theory for Study of decision problems in which a group has to make the decision The decision
Intro to Contemporary Math
 Intro to Contemporary Math Independence of Irrelevant Alternatives Criteria Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Independence of Irrelevant Alternatives Criteria
Intro to Contemporary Math Independence of Irrelevant Alternatives Criteria Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Independence of Irrelevant Alternatives Criteria
CS 886: Multiagent Systems. Fall 2016 Kate Larson
 CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
Math116Chap1VotingPart2.notebook January 12, Part II. Other Methods of Voting and Other "Fairness Criteria"
 Part II Other Methods of Voting and Other "Fairness Criteria" Plurality with Elimination Method Round 1. Count the first place votes for each candidate, just as you would in the plurality method. If a
Part II Other Methods of Voting and Other "Fairness Criteria" Plurality with Elimination Method Round 1. Count the first place votes for each candidate, just as you would in the plurality method. If a
Sect 13.2 Flaws of Voting Methods
 218 Sect 13.2 Flaws of Voting Methods From an example the previous section, we had 48 sports writers rank the top four Spurs players of all time. Below is the preference table. Number of votes 20 14 10
218 Sect 13.2 Flaws of Voting Methods From an example the previous section, we had 48 sports writers rank the top four Spurs players of all time. Below is the preference table. Number of votes 20 14 10
Introduction to the Theory of Voting
 November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
MATH 1340 Mathematics & Politics
 MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
Problems with Group Decision Making
 Problems with Group Decision Making There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Problems with Group Decision Making There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Many Social Choice Rules
 Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
Math Circle Voting Methods Practice. March 31, 2013
 Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
Voting System: elections
 Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
Introduction to Theory of Voting. Chapter 2 of Computational Social Choice by William Zwicker
 Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Social Choice Theory. Denis Bouyssou CNRS LAMSADE
 A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
Lecture 12: Topics in Voting Theory
 Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
Math for Liberal Studies
 Math for Liberal Studies There are many more methods for determining the winner of an election with more than two candidates We will only discuss a few more: sequential pairwise voting contingency voting
Math for Liberal Studies There are many more methods for determining the winner of an election with more than two candidates We will only discuss a few more: sequential pairwise voting contingency voting
Voting Protocols. Introduction. Social choice: preference aggregation Our settings. Voting protocols are examples of social choice mechanisms
 Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
Safe Votes, Sincere Votes, and Strategizing
 Safe Votes, Sincere Votes, and Strategizing Rohit Parikh Eric Pacuit April 7, 2005 Abstract: We examine the basic notion of strategizing in the statement of the Gibbard-Satterthwaite theorem and note that
Safe Votes, Sincere Votes, and Strategizing Rohit Parikh Eric Pacuit April 7, 2005 Abstract: We examine the basic notion of strategizing in the statement of the Gibbard-Satterthwaite theorem and note that
Syllabus update: Now keeping best 3 of 4 tests
 Syllabus update: Now keeping best 3 of 4 tests The answer was 22. Recall order of operations: Parentheses, exponents, multiplication/division, addition/subtraction. PEMDAS Please Excuse My Dear Aunt Sally
Syllabus update: Now keeping best 3 of 4 tests The answer was 22. Recall order of operations: Parentheses, exponents, multiplication/division, addition/subtraction. PEMDAS Please Excuse My Dear Aunt Sally
VOTING SYSTEMS AND ARROW S THEOREM
 VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
that changes needed to be made when electing their Presidential nominee. Iowa, at the time had a
 Part I The Iowa caucuses are perhaps the most important yet mysterious contest in American politics. It all began after the 1968 Democratic National Convention protest, the party decided that changes needed
Part I The Iowa caucuses are perhaps the most important yet mysterious contest in American politics. It all began after the 1968 Democratic National Convention protest, the party decided that changes needed
Problems with Group Decision Making
 Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Voting. Hannu Nurmi. Game Theory and Models of Voting. Public Choice Research Centre and Department of Political Science University of Turku
 Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Game Theory and Models of points the history of voting procedures is highly discontinuous, early contributions
Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Game Theory and Models of points the history of voting procedures is highly discontinuous, early contributions
Math for Liberal Arts MAT 110: Chapter 12 Notes
 Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
: It is mathematically impossible for a democratic voting method to satisfy all of the fairness criteria was proven in 1949.
 Chapter 1 Notes from Voting Theory: the mathematics of the intricacies and subtleties of how voting is done and the votes are counted. In the early 20 th century, social scientists and mathematicians working
Chapter 1 Notes from Voting Theory: the mathematics of the intricacies and subtleties of how voting is done and the votes are counted. In the early 20 th century, social scientists and mathematicians working
The Math of Rational Choice - Math 100 Spring 2015
 The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
The actual midterm will probably not be multiple choice. You should also study your notes, the textbook, and the homework.
 Math 101 Practice First Midterm The actual midterm will probably not be multiple choice. You should also study your notes, the textbook, and the homework. Answers are on the last page. MULTIPLE CHOICE.
Math 101 Practice First Midterm The actual midterm will probably not be multiple choice. You should also study your notes, the textbook, and the homework. Answers are on the last page. MULTIPLE CHOICE.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Chapter 1 Review SHORT ANSWER. Answer each question. Circle your final answer. Show all work. Determine whether any of the listed candidates has a majority. 1) Four candidates running for congress receive
Chapter 1 Review SHORT ANSWER. Answer each question. Circle your final answer. Show all work. Determine whether any of the listed candidates has a majority. 1) Four candidates running for congress receive
CSC304 Lecture 16. Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting. CSC304 - Nisarg Shah 1
 CSC304 Lecture 16 Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting CSC304 - Nisarg Shah 1 Announcements Assignment 2 was due today at 3pm If you have grace credits left (check MarkUs),
CSC304 Lecture 16 Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting CSC304 - Nisarg Shah 1 Announcements Assignment 2 was due today at 3pm If you have grace credits left (check MarkUs),
CSC304 Lecture 14. Begin Computational Social Choice: Voting 1: Introduction, Axioms, Rules. CSC304 - Nisarg Shah 1
 CSC304 Lecture 14 Begin Computational Social Choice: Voting 1: Introduction, Axioms, Rules CSC304 - Nisarg Shah 1 Social Choice Theory Mathematical theory for aggregating individual preferences into collective
CSC304 Lecture 14 Begin Computational Social Choice: Voting 1: Introduction, Axioms, Rules CSC304 - Nisarg Shah 1 Social Choice Theory Mathematical theory for aggregating individual preferences into collective
Warm-up Day 3 Given these preference schedules, identify the Plurality, Borda, Runoff, Sequential Runoff, and Condorcet winners.
 Warm-up Day 3 Given these preference schedules, identify the Plurality, Borda, Runoff, Sequential Runoff, and Condorcet winners. Plurality: Borda: Runoff: Seq. Runoff: Condorcet: Warm-Up Continues -> Warm-up
Warm-up Day 3 Given these preference schedules, identify the Plurality, Borda, Runoff, Sequential Runoff, and Condorcet winners. Plurality: Borda: Runoff: Seq. Runoff: Condorcet: Warm-Up Continues -> Warm-up
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
Rationality & Social Choice. Dougherty, POLS 8000
 Rationality & Social Choice Dougherty, POLS 8000 Social Choice A. Background 1. Social Choice examines how to aggregate individual preferences fairly. a. Voting is an example. b. Think of yourself writing
Rationality & Social Choice Dougherty, POLS 8000 Social Choice A. Background 1. Social Choice examines how to aggregate individual preferences fairly. a. Voting is an example. b. Think of yourself writing
The mathematics of voting, power, and sharing Part 1
 The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
The Mathematics of Voting
 Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
Voter Sovereignty and Election Outcomes
 Voter Sovereignty and Election Outcomes Steven J. Brams Department of Politics New York University New York, NY 10003 USA steven.brams@nyu.edu M. Remzi Sanver Department of Economics Istanbul Bilgi University
Voter Sovereignty and Election Outcomes Steven J. Brams Department of Politics New York University New York, NY 10003 USA steven.brams@nyu.edu M. Remzi Sanver Department of Economics Istanbul Bilgi University
The search for a perfect voting system. MATH 105: Contemporary Mathematics. University of Louisville. October 31, 2017
 The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
Chapter 9: Social Choice: The Impossible Dream
 Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
Critical Strategies Under Approval Voting: Who Gets Ruled In And Ruled Out
 Critical Strategies Under Approval Voting: Who Gets Ruled In And Ruled Out Steven J. Brams Department of Politics New York University New York, NY 10003 USA steven.brams@nyu.edu M. Remzi Sanver Department
Critical Strategies Under Approval Voting: Who Gets Ruled In And Ruled Out Steven J. Brams Department of Politics New York University New York, NY 10003 USA steven.brams@nyu.edu M. Remzi Sanver Department
Voting and preference aggregation
 Voting and preference aggregation CSC200 Lecture 38 March 14, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading for
Voting and preference aggregation CSC200 Lecture 38 March 14, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading for
Approaches to Voting Systems
 Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
Voting and preference aggregation
 Voting and preference aggregation CSC304 Lecture 20 November 23, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading
Voting and preference aggregation CSC304 Lecture 20 November 23, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading
Arrow s Conditions and Approval Voting. Which group-ranking method is best?
 Arrow s Conditions and Approval Voting Which group-ranking method is best? Paradoxes When a group ranking results in an unexpected winner, the situation is known as a paradox. A special type of paradox
Arrow s Conditions and Approval Voting Which group-ranking method is best? Paradoxes When a group ranking results in an unexpected winner, the situation is known as a paradox. A special type of paradox
A Study of Approval voting on Large Poisson Games
 A Study of Approval voting on Large Poisson Games Ecole Polytechnique Simposio de Analisis Económico December 2008 Matías Núñez () A Study of Approval voting on Large Poisson Games 1 / 15 A controversy
A Study of Approval voting on Large Poisson Games Ecole Polytechnique Simposio de Analisis Económico December 2008 Matías Núñez () A Study of Approval voting on Large Poisson Games 1 / 15 A controversy
Decision making and problem solving Lecture 10. Group techniques Voting MAVT for group decisions
 Decision making and problem solving Lecture 10 Group techniques Voting MAVT for group decisions Motivation Thus far we have assumed that Objectives, attributes/criteria, and decision alternatives are given
Decision making and problem solving Lecture 10 Group techniques Voting MAVT for group decisions Motivation Thus far we have assumed that Objectives, attributes/criteria, and decision alternatives are given
The Problem with Majority Rule. Shepsle and Bonchek Chapter 4
 The Problem with Majority Rule Shepsle and Bonchek Chapter 4 Majority Rule is problematic 1. Who s the majority? 2. Sometimes there is no decisive winner Condorcet s paradox: A group composed of individuals
The Problem with Majority Rule Shepsle and Bonchek Chapter 4 Majority Rule is problematic 1. Who s the majority? 2. Sometimes there is no decisive winner Condorcet s paradox: A group composed of individuals
Rock the Vote or Vote The Rock
 Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
Voting Systems for Social Choice
 Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku 20014 Turku Finland Voting Systems for Social Choice Springer The author thanks D. Marc Kilgour and Colin
Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku 20014 Turku Finland Voting Systems for Social Choice Springer The author thanks D. Marc Kilgour and Colin
Mathematics of Voting Systems. Tanya Leise Mathematics & Statistics Amherst College
 Mathematics of Voting Systems Tanya Leise Mathematics & Statistics Amherst College Arrow s Impossibility Theorem 1) No special treatment of particular voters or candidates 2) Transitivity A>B and B>C implies
Mathematics of Voting Systems Tanya Leise Mathematics & Statistics Amherst College Arrow s Impossibility Theorem 1) No special treatment of particular voters or candidates 2) Transitivity A>B and B>C implies
