How should we count the votes?
|
|
|
- Felicity Fitzgerald
- 6 years ago
- Views:
Transcription
1 How should we count the votes? Bruce P. Conrad January 16, 2008 Were the Iowa caucuses undemocratic? Many politicians, pundits, and reporters thought so in the weeks leading up to the January 3, 2008 event. Polls couldn t predict the outcome, frustrating reporters. In the case of the Democrats, the ballot wasn t secret. To participate a voter had to take a few hours off on a Thursday evening. Turnout statewide although unusually strong for this event was only 17% of registered voters. The critics prefer a primary election. A mathematician cannot comment on the cited weaknesses of the caucuses, but elections with more than two candidates are a thorny problem hat has been the subject of study for centuries. There is still no consensus among the experts. To see the problem clearly, consider this example. Fifteen judges are rating figure skaters A, B, and C. Six judges say the performance of A was best, B second; five say C was best, B second; and the remaining four say B was best, C second. Who gets the gold medal, and who the silver? The plurality system gives first place to the competitor who gets ranked first by the greatest number of judges; second place goes to the one who gets the next to the most first ranking votes, and so on. Plurality is used to decide most elections in the United States. For the figure skaters, the plurality result is A C B. Because no skater is first-ranked by a majority, the judges might try a runoff election. Since B has the fewest first-place votes, she is eliminated in the first round, and ranks last. The four judges who favored B transfer their votes to their second choice, C. But then C beats A, 9 6 for first place, resulting in the ranking C A B. The International Skating Union (ISU) has rules to decide competitions. Skaters are ranked according to the number of skaters that a majority of the judges rank below them. Thus, A is not ranked above any skater by a majority, because 9 judges place her last. B is ranked above A by those 9 judges, and is ranked above C by 10. Thus B gets credit for being ranked ahead of 1
2 two other skaters. C is ranked ahead of A by a majority of judges, but is not ranked ahead of B by a majority. The official result would therefore be: B, gold; C, silver; and A, bronze. Depending on the method used to count the votes, any one of the skaters could win the gold medal. Thus, there is reason to worry about how a vote can find the best of more than two alternatives. Perhaps caucusing, with interaction and discussion between voters instead of a rigid algorithm, has some merit after all. Election algorithms An election involves with a set C of candidates, and a set V of voters. Each voter has made a preference list of the candidates in the order that he or she prefers. We will use the notation U > V to mean that U is preferred to V on an individual preference list, and U V to mean that the election algorithm in question places U ahead of V. The ranking > on each preference list must be transitive, complete, and without ties. That means that for two candidates Y and Z either Y > Z or Z > Y (but not both), and (X > T )&(T > Z) implies X > Z. For example, a Democrat who participated in an Iowa caucus might have preferred Obama, with second choice Clinton, third choice Edwards, fourth choice Richardson, fifth choice Biden, sixth choice Dodd, seventh choice Kucinich, and last choice Gravel. Her preference list would be O > C > E > R > B > D > K > G. Let P be the set of all orderings of C; that is, the set of all possible preference lists. A voting profile is defined to be a function p : V P that associates each voter with his or her preference list. An election algorithm is a rule that, when given a profile, determines the winner of the election. If we call the algorithm E, then the input would be a voting profile p and the output would be the winning candidate, or in case of a tie, a set of winning candidates. In the figure skating contest, the output of the election algorithm should be an ordering of the candidates that is, an element of P. In case of a tie, the output would be a subset of P. The most undemocratic election algorithm is dictatorship. A particular voter, D, is the dictator. The winner is the dictator s choice. For example, if the dictator is scoring a gymnastics contest, then for any profile p, E(p) = p(d), the dictator s personal ranking. The other judges votes are not used. We have seen the plurality algorithm. Its obvious flaw is that it ignores information that may be relevant. With 5 candidates, it is possible that the winner may have only 30% of the first-place votes, and it could be that the 2
3 voters who did not rank the winner first might have ranked him last. In an effort to look below the first-place rankings, many runoff algorithms have been invented. These always involve repeated elections, eliminating at each stage one or more candidates. With Instant runoff voting, or IRV, each voter enters his or her entire preference list on a ballot. The runoff elections can be conducted by the computer, so it is unnecessary to have repeated trips to the polls. Also, voters can t change their priorities at each stage. With IRV, as soon as a candidate receives a majority of the first place votes, then he or she wins. Until a winner is chosen, the candidate with the fewest first-place votes at any stage is eliminated, and all voters who ranked that candidate first would have their votes transferred to their next choice. The runoff algorithms are not monotone: in other words a voter can cause a winning candidate to lose by changing her preference list in that candidate s favor. Here is a profile with that property: 6 voters X > Y > Z 5 voters Y > X > Z 6 voters Z > Y > X With this profile, X wins an IRV election. But suppose two of the voters with preference Z > Y > X switch to X > Z > Y. They thought they were helping X, but they cause Y to win, and X to lose! Ramon Llull ( ) wrote the first known study of multicandidate elections. In the 1780 s, elections became a topic of interest in the French Academy of Sciences. One academician, Jean Charles de Borda ( ) who was an applied mathematician and naval officer best known for his contributions to fluid mechanics, developed an algorithm that is now known as the Borda count. For a candidate X, find, for each opponent Y i the number n i of voters who prefer X to Y i. The Borda count for X is then the sum of the numbers n i. The algorithm then ranks the candidates in decreasing order of Borda count. For the figure skating competition example, A has two opponents below her on 6 preference lists: her Borda count is 12. B has one opponent below her on 11 preference lists, and two below her on 4 preference lists, so her Borda count is = 19. Similarly, C has a Borda count of 14. Thus the skaters would be ranked B C A, which agrees with the ISU result. The marquis de Condorcet ( ) is another French academician who is remembered for his contributions to the theory of elections. A mathematician specializing in probability theory, Condorcet objected to Borda s algorithm and promoted his own. We will say that a candidate C who is preferred by a majority of the voters to every other candidate Y i is a 3
4 Condorcet winner. For example, in the figure skating example, B is a Condorcet winner. According to the ISU rules, a Condorcet winner will win the gold medal, because he or she will be ranked higher than any single opponent in a head to head comparison by a majority of the judges. Condorcet s criticism of Borda s algorithm was that it did not guarantee victory for the Condorcet winner. In the following profile, the Condorcet ranking is P Q R while the Borda ranking is Q P R. 6 voters P > Q > R 3 voters Q > P > R 2 voters Q > R > P Condorcet winners can and sometimes doalso lose elections decided by plurality or runoffs. The figure skating example shows this, and here is a real-world example: In the 2007 French presidential election, the top candidates in the first round were Nicolas Sarcozy, François Bayrou, and Ségolène Royal. Bayrou was eliminated in the first round, and Sarcozy went on to win the presidency in the runoff by a margin of 53 47%. Pre-election polling indicated that Bayrou could defeat Royal, 58 42%, and that he could defeat Sarcozy, 55 45%, in head-to-head contests. If these polls are to be believed (and of course polling is notoriously unreliable), Bayrou was the Condorcet winner. The polling data can also be used to estimate the Borda count. The table below shows percentage of the electorate that preferred the candidate of a particular row over an opponent in the column. The column on the right is a sum of the percentages in the rows, and is the Borda count, expressed as a percentage of the number of voters. Bayrou Royal Sarcozy Borda count Bayrou 58% 55% 113% Royal 42% 47% 89% Sarcozy 45% 53% 98% Based on polling data, it seems that Bayrou was also the Borda count winner. Condorcet s idea has a complication which he addressed. It can happen that there is no Condorcet winner at all. Here is a profile that demonstrates this. 5 voters U > V > W 4 voters V > W > U 2 voters V > U > W 6 voters W > U > V 4
5 When we match two candidates, the one who loses is not a Condorcet winner, because to qualify one must win all matches. In this case, you can see that U V (this means a majority prefers U to V ), so V is a Condorcet nonwinner. Also V W by an 11 6 margin. However, if we match U against W, thinking that U will win, we are in for a surprise, because W U, We have discovered a Condorcet cycle, U V W U. These Condorcet cycles are the source of much of the confusion associated with multicandidate elections. If a Condorcet cycle occurs in the judges ranking for a figure skating competition, the skaters involved in the cycle would be tied. The ISU rules specify that when this happens, the Borda count should be used to break the tie. In the {U, V, W } profile, the Borda counts are U, 18; V, 17; and W, 16. The ISU ranking is therefore U V W. Have the skaters figured it out? Should we just elect politicians by the ISU rules? Before we close the book on this subject, let s consider two additional criteria that seem reasonable for an election algorithm to satisfy. The Theorem of Arrow Here is an unfair algorithm, called the agenda algorithm, because it uses an ordered list of the candidates, called the agenda. If the agenda is C 1,..., C n, then the algorithm matches C 1 against C 2, the winner of that match takes on C 3, and so on. When the end of the agenda is reached there will be one survivor, who is declared the winner. This procedure will always select a Condorcet winner if there is one, since he or she is the only candidate who can t been eliminated. When the profile has no Condorcet winner, it is advantageous to be last on the agenda then you only have to win one contest. This makes the agenda algorithm unfair, but it has another problem, because it fails a test that was devised by Vilfredo Pareto ( ): If the voters unanimously prefer candidate C 1 to candidate C 2 and C 1 is not a winner, then C 2 must not win, either. Here is an example that shows the agenda algorithm fails Pareto s test. Three princes, A, B and C, are holding an election to decide who should be monarch. Prince B announces that his dog, D, is also a candidate. These are the preference lists. Prince A Prince B Prince C A > B > D > C B > D > C > A C > A > B > D 5
6 Notice that each prince prefers B to D, and that with the agenda A, B, C, D, the dog wins. The dog s advantage was being last on the agenda. Any one of the princes could also be the winner just rearrange the agenda. This algorithm is only used by legislative committees, and the ability to set the agenda is one of the perquisites of the chairperson. The other algorithms that we have discussed, even dictatorship, pass the Pareto test. Independence from irrelevant alternatives (IIA). A voter who submits a preference list that does not reflect his or her true priorities is said to be voting insincerely. An algorithm that does not have the following property, called IIA, will offer opportunities to vote insincerely. Given that A is a winner, and B an non-winner then B cannot become a winner and A a non-winner as a result of changes in one or more voters preference lists, as long as no voter reverses the relative positions of A and B. Suppose that in the first round of the 2007 election in France, those who supported Royal had preference lists Royal > Bayrou > Sarcozy. If these voters voted insincerely by moving Royal to second place and voting for Bayrou, then Bayrou would have won. No one would have switched their preference between Bayrou and Sarcozy, so the runoff method is not IIA. The plurality algorithm is also not IIA. Suppose an election involving a Democrat D, a Republican R and a third-party candidate T, with the following profile: 23% of voters D > T > R 20% of voters D > R > T 40% of voters R > D > T 5% of voters R > T > D 12% of voters T > D > R If everyone votes sincerely, the Republican will win with 45% of the vote. The third-party voters realize the contest between the Democrat and Republican is close, and their candidate has no chance. If more than one-sixth of them vote insincerely for the Democrat, they will cause the Democrat to win, and the Republican to lose. No one has changed their relative preference between R and D, so plurality fails the IIA test. In work that reawakened interest in the election decision problem, the economist Kenneth Arrow proved the following theorem. For a short proof (actually three of them), see [3]. Theorem (Arrow, 1951) There is no election algorithm other than dictatorship that is applicable 6
7 to elections with more than two candidates and satisfies the Pareto and IIA conditions. Arrow s theorem raises questions abut using any election algorithm based on voter preference lists. Range voting is an alternative to profile-based election algorithms. Let N be a positive integer; usually 9 or 99 is used. A range ballot is a list in which a voter has marked each candidate s name with a number from 0 to N to indicate a preference or with a blank to indicate no opinion. The numbers don t have to be distinct. The winner is the candidate who has the greatest average score. In computing the average, blank votes are ignored. Thus a 0 is a vote against a candidate because it affects the candidate s average, but a blank vote is just an abstention. Because a candidate who is completely unknown might get a high score on one ballot (his own) and blank on everyone else s, there is a quorum rule: The total score of the winner must be at least half of the greatest total score received by any candidate. Range voting is relatively untested in general elections, and opponents of this method caution that there would be insincere voting, in which most voters would rate their most favored candidates with N and rate all others 0. If this behavior were prevalent, range voting would produce a result identical to the plurality algorithm. Proponents of range voting point out that the supporters of a third party candidate would not have to forsake their favorite: they could rate her with N and give the major candidate whom they find least offensive a lower score. There is an organization that promotes range voting, rangevoting.org. Approval voting is an alternative that is simpler than range voting. Each voter is asked to check the names of the candidates whom he or she approves on the ballot. A voter may approve as many candidates as he or she thinks is appropriate. The candidate with the largest number of approvals wins. Approval voting is not the same as range voting with N = 1, because there is no way to indicate abstention, as one can in range voting. The principal objection to approval voting is that voters will approve their favorite candidates, and not approve any other candidates. The winner would be the plurality winner. However, a quorum condition could address this problem by requiring that the winner must have the approval of more than half of the voters. If a quorum is not achieved by any candidate, the election would be repeated. S. Brams and P. Fishburn have written a book [1] advocating approval voting. By avoiding voter preference lists, range and approval voting offer voters 7
8 the chance to indicate which candidates are acceptable. A preference list does not have that information, since it doesn t say where the voter would draw a line. Nevertheless, it would be unscientific to predict that either range or approval voting will solve our electoral problems without doing some experiments first. Among election algorithms based on profiles, the favorites among mathematicians are the Borda count and an algorithm originally described, albeit not very clearly, by Borda s rival, the marquis. Perhaps the strangest part of this story is that the controversy between Condorcet and Borda is still unsettled after more than 200 years. Meanwhile, the most prevalent election algorithms, plurality and various sorts of runoff methods, although known to be inferior, are still the most widely used. The Borda count belongs to a class of election algorithms called positional algorithms, which are constructed as follows. Suppose that there are c candidates, and let s = (s 1, s 2,..., s c ) R c be a fixed vector such that s 1 s 2 s c 0. We call s the scoring vector. For each candidate C i the score would be the sum s 1 the number of voters ranking C i first, plus s 2 the number of voters ranking C i second, and so on, until s c the number of voters ranking C i last. Candidates are ranked by score in descending order. The scoring vector s = (1, 0, 0,..., 0) gives C i the number of voters who ranked him first as score, and in this case the ranking is the same as the plurality method. If s = b c = (c 1, c 2,..., 0) a candidate s score is his or her Borda count. D. Saari showed in [4] that for most scoring vectors, positional algorithms can exhibit very strange behavior. Unless the scoring vector is carefully chosen, it is possible to specify orderings for all of the subsets of C, and then find a voting profile such that the ranking of each subset is the specified ordering. For example, suppose that C = {A, B, C, D}. We could specify, for each of the 11 subsets of C that have more than one element, a randomly chosen ordering, something like A D B C, C B D, D B A, C A, etc. Then there exists a voting profile that would give the first ordering; yet if A dropped out, the second ordering would be the result; if C dropped out, the result would the the third ordering; and in A v. C headto-head, C would win. In particular this applies to the plurality algorithm. Saari has written a book [4], aptly titled Chaotic elections. Saari found that the Borda count scoring vector b c was an exception. His theorem applies to most scoring vectors, but not to b c. Although still subject to Arrow s theorem, the Borda count is a relatively well-behaved election algorithm. 8
9 We have seen an example where the majority of the voters had the same preference list, P > Q > R; yet the Borda ranking was Q P R. This brings to mind Condorcet s algorithm, which, with eight other algorithms that satisfy the Condorcet condition, are reviewed in [2]. If there are n candidates, then there are n(n 1)/2 pairs of candidates, and thus 2 n(n 1)/2 possible sets of pairwise orderings, or opinions. An opinion, C i C j, is a statement that in a majority of the preference lists, voters preferred C i to C j. The margin of the opinion C i C j is defined to be the number of voters who had C i > C j on their preference lists, minus the number who had C j > C i. For n = 3 we have 3 pairings and 8 possible sets of opinions. Since the number of total rankings is 3! = 6, two of the sets of opinions cannot be consistent with a total ordering: these are Condorcet cycles. Condorcet s assumption is that the purpose of voting is to find the true ranking of the candidates. If there is a Condorcet cycle, some voters must have erred, and the correct ranking is the one that can be achieved by changing the fewest voter preferences. If a Condorcet cycle occurs in a three-candidate election, delete the opinion with the least margin. If we apply this method to the cycle involving the candidates U, V, and W, (see above) the following list occurs (the margin appears above each relation). U 5 V 9 W 3 U and hence the Condorcet ranking is the same as the Borda ranking, U V W. Notice that in deleting the opinion W U we have in effect reversed it, because it is now implied by our result, U V W. Condorcet s algorithm requires a modification if there are four or more candidates. P. Young [8] suggested that some of the opinions should be reversed to eliminate cycles and produce a complete and transitive ranking of the candidates. The sum of the margins of the reversed opinions must be as small as possible. This algorithm has also been described by John Kemeny, and is listed under his name in [2]. This Condorcet-Kemeny (CK) algorithm gives the total ordering of the candidates that is closest to the profile, in the sense that it can be made with the fewest reversals of priority on voter preference lists. It does, however, involve some vote changing. In [7], P. Young proved that as a ranking algorithm, CK is the only one satisfying Condorcet s criterion with the following additional properties: It treats candidates equally and it treats voters equally; it passes Pareto s test; it is consistent in the sense that if the voters are divided into two disjoint subsets and both give the same ranking by this algorithm, then 9
10 the combined set of voters will also give this ranking; and it is locally IIA (LIIA). Suppose that an election algorithm has obtained a ranking of candidates. An interval in that ranking is a subset I C such that if C 1, C 3 I and C 1 C 2 C 3 then C 2 I. The algorithm is LIIA if the ranking within any interval will remain unchanged if candidates who are not in the interval drop out. This is not the case with the Borda count, and Young points out that that this makes the Borda algorithm vulnerable to manipulation, by the introduction of low-ranked candidates on the ballot. The CK algorithm has been compared with the Borda count by Saari and Merlin and in [6], using geometric methods. They note that Borda counts ignore Condorcet cycles, and of course the Borda ranking is achieved without switching any voter preferences. Their analysis includes a geometric explanation of the differences between the algorithms. Here is a sample theorem from [6], which makes a precise statement of how much the Borda count and CK rankings can differ. Suppose that two rankings of C are given. Then there is a voting profile such that the first ranking is by the Borda count, and the second is the CK ranking, if and only if the first and last candidates in one ranking are not reversed in order in the other. What should we do? There are points in favor of deciding elections by Approval or Range voting, or by the Borda or CK algorithms. We have little experience with any of these, but all have advantages over the methods that are now widely used. In the political arena, it will be very difficult to implement any of these methods, simply because politicians who don t want to be faced with a new system. Another hurdle that applies to all except approval voting is the added complexity of the ballot. If I were dictator for a moment, I would require some experiments to see what works. Probably we can t choose a better election algorithm by voting there are too many candidates. References [1] Brams, Steven and Peter C. Fishburn, Approval voting, second edition (2007), Springer-Verlag New York. [2] Fishburn, Peter C., Condorcet social choice functions, SIAM Journal on Applied Mathematics 33 (1977) pp
11 [3] Geanakoplos, John, Three Brief Proofs of Arrow s Impossibility Theorem (June 2001). Yale Cowles Foundation Discussion Paper No. 1123RRR. Available at SSRN: [4] Saari, Donald G., A dictionary for voting paradoxes, Journal of Economic Theory 48 (1989) pp [5] Chaotic Elections! A Mathematician Looks at Voting. American Math. Society, [6] and Vincent R. Merlin, A geometric examination of Kemeny s rule, Soc Choice Welfare 17 (2000) pp [7] Young, Peyton, Optimal voting rules, The Journal of Economic Perspectives, 9 (1995), pp [8], Condorcet s theory of voting The American Political Science Review, 82 (1988), pp
Arrow s Impossibility Theorem
 Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
1.6 Arrow s Impossibility Theorem
 1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Desirable properties of social choice procedures. We now outline a number of properties that are desirable for these social choice procedures:
 Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Fairness Criteria. Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election.
 Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Chapter 1 Practice Test Questions
 0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
9.3 Other Voting Systems for Three or More Candidates
 9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
Social Choice: The Impossible Dream. Check off these skills when you feel that you have mastered them.
 Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
answers to some of the sample exercises : Public Choice
 answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
Fairness Criteria. Review: Election Methods
 Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
Recall: Properties of ranking rules. Recall: Properties of ranking rules. Kenneth Arrow. Recall: Properties of ranking rules. Strategically vulnerable
 Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
VOTING SYSTEMS AND ARROW S THEOREM
 VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
The Mathematics of Voting
 Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
Elections with Only 2 Alternatives
 Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Voting Criteria April
 Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
MATH 1340 Mathematics & Politics
 MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
Rock the Vote or Vote The Rock
 Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
The search for a perfect voting system. MATH 105: Contemporary Mathematics. University of Louisville. October 31, 2017
 The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
Head-to-Head Winner. To decide if a Head-to-Head winner exists: Every candidate is matched on a one-on-one basis with every other candidate.
 Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
SOCIAL CHOICES (Voting Methods) THE PROBLEM. Social Choice and Voting. Terminologies
 SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
Many Social Choice Rules
 Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
(67686) Mathematical Foundations of AI June 18, Lecture 6
 (67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
(67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
Voting: Issues, Problems, and Systems, Continued
 Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory
 MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
that changes needed to be made when electing their Presidential nominee. Iowa, at the time had a
 Part I The Iowa caucuses are perhaps the most important yet mysterious contest in American politics. It all began after the 1968 Democratic National Convention protest, the party decided that changes needed
Part I The Iowa caucuses are perhaps the most important yet mysterious contest in American politics. It all began after the 1968 Democratic National Convention protest, the party decided that changes needed
Mathematics and Social Choice Theory. Topic 4 Voting methods with more than 2 alternatives. 4.1 Social choice procedures
 Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Voting Methods for Municipal Elections: Propaganda, Field Experiments and what USA voters want from an Election Algorithm
 Voting Methods for Municipal Elections: Propaganda, Field Experiments and what USA voters want from an Election Algorithm Kathryn Lenz, Mathematics and Statistics Department, University of Minnesota Duluth
Voting Methods for Municipal Elections: Propaganda, Field Experiments and what USA voters want from an Election Algorithm Kathryn Lenz, Mathematics and Statistics Department, University of Minnesota Duluth
VOTING TO ELECT A SINGLE CANDIDATE
 N. R. Miller 05/01/97 5 th rev. 8/22/06 VOTING TO ELECT A SINGLE CANDIDATE This discussion focuses on single-winner elections, in which a single candidate is elected from a field of two or more candidates.
N. R. Miller 05/01/97 5 th rev. 8/22/06 VOTING TO ELECT A SINGLE CANDIDATE This discussion focuses on single-winner elections, in which a single candidate is elected from a field of two or more candidates.
Computational Social Choice: Spring 2007
 Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Voting Criteria: Majority Criterion Condorcet Criterion Monotonicity Criterion Independence of Irrelevant Alternatives Criterion
 We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
Mathematical Thinking. Chapter 9 Voting Systems
 Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
The Manipulability of Voting Systems. Check off these skills when you feel that you have mastered them.
 Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
Rationality of Voting and Voting Systems: Lecture II
 Rationality of Voting and Voting Systems: Lecture II Rationality of Voting Systems Hannu Nurmi Department of Political Science University of Turku Three Lectures at National Research University Higher
Rationality of Voting and Voting Systems: Lecture II Rationality of Voting Systems Hannu Nurmi Department of Political Science University of Turku Three Lectures at National Research University Higher
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Main idea: Voting systems matter.
 Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
Arrow s Impossibility Theorem on Social Choice Systems
 Arrow s Impossibility Theorem on Social Choice Systems Ashvin A. Swaminathan January 11, 2013 Abstract Social choice theory is a field that concerns methods of aggregating individual interests to determine
Arrow s Impossibility Theorem on Social Choice Systems Ashvin A. Swaminathan January 11, 2013 Abstract Social choice theory is a field that concerns methods of aggregating individual interests to determine
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
Measuring Fairness. Paul Koester () MA 111, Voting Theory September 7, / 25
 Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
The Mathematics of Voting
 The Mathematics of Voting Voting Methods Summary Last time, we considered elections for Math Club President from among four candidates: Alisha (A), Boris (B), Carmen (C), and Dave (D). All 37 voters submitted
The Mathematics of Voting Voting Methods Summary Last time, we considered elections for Math Club President from among four candidates: Alisha (A), Boris (B), Carmen (C), and Dave (D). All 37 voters submitted
Exercises For DATA AND DECISIONS. Part I Voting
 Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Voting: Issues, Problems, and Systems. Voting I 1/36
 Voting: Issues, Problems, and Systems Voting I 1/36 Each even year every member of the house is up for election and about a third of the senate seats are up for grabs. Most people do not realize that there
Voting: Issues, Problems, and Systems Voting I 1/36 Each even year every member of the house is up for election and about a third of the senate seats are up for grabs. Most people do not realize that there
Chapter 9: Social Choice: The Impossible Dream
 Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections
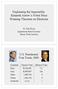 Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Kybernetika. Robert Bystrický Different approaches to weighted voting systems based on preferential positions
 Kybernetika Robert Bystrický Different approaches to weighted voting systems based on preferential positions Kybernetika, Vol. 48 (2012), No. 3, 536--549 Persistent URL: http://dml.cz/dmlcz/142955 Terms
Kybernetika Robert Bystrický Different approaches to weighted voting systems based on preferential positions Kybernetika, Vol. 48 (2012), No. 3, 536--549 Persistent URL: http://dml.cz/dmlcz/142955 Terms
The Mathematics of Voting. The Mathematics of Voting
 1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
Introduction to the Theory of Voting
 November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
Math Circle Voting Methods Practice. March 31, 2013
 Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
Introduction to Theory of Voting. Chapter 2 of Computational Social Choice by William Zwicker
 Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
12.2 Defects in Voting Methods
 12.2 Defects in Voting Methods Recall the different Voting Methods: 1. Plurality - one vote to one candidate, the others get nothing The remaining three use a preference ballot, where all candidates are
12.2 Defects in Voting Methods Recall the different Voting Methods: 1. Plurality - one vote to one candidate, the others get nothing The remaining three use a preference ballot, where all candidates are
The Math of Rational Choice - Math 100 Spring 2015
 The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
Today s plan: Section : Plurality with Elimination Method and a second Fairness Criterion: The Monotocity Criterion.
 1 Today s plan: Section 1.2.4. : Plurality with Elimination Method and a second Fairness Criterion: The Monotocity Criterion. 2 Plurality with Elimination is a third voting method. It is more complicated
1 Today s plan: Section 1.2.4. : Plurality with Elimination Method and a second Fairness Criterion: The Monotocity Criterion. 2 Plurality with Elimination is a third voting method. It is more complicated
Approaches to Voting Systems
 Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
In deciding upon a winner, there is always one main goal: to reflect the preferences of the people in the most fair way possible.
 Voting Theory 1 Voting Theory In many decision making situations, it is necessary to gather the group consensus. This happens when a group of friends decides which movie to watch, when a company decides
Voting Theory 1 Voting Theory In many decision making situations, it is necessary to gather the group consensus. This happens when a group of friends decides which movie to watch, when a company decides
Social Choice & Mechanism Design
 Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
Math for Liberal Studies
 Math for Liberal Studies There are many more methods for determining the winner of an election with more than two candidates We will only discuss a few more: sequential pairwise voting contingency voting
Math for Liberal Studies There are many more methods for determining the winner of an election with more than two candidates We will only discuss a few more: sequential pairwise voting contingency voting
Chapter 10. The Manipulability of Voting Systems. For All Practical Purposes: Effective Teaching. Chapter Briefing
 Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
Make the Math Club Great Again! The Mathematics of Democratic Voting
 Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
Lecture 12: Topics in Voting Theory
 Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
Math116Chap1VotingPart2.notebook January 12, Part II. Other Methods of Voting and Other "Fairness Criteria"
 Part II Other Methods of Voting and Other "Fairness Criteria" Plurality with Elimination Method Round 1. Count the first place votes for each candidate, just as you would in the plurality method. If a
Part II Other Methods of Voting and Other "Fairness Criteria" Plurality with Elimination Method Round 1. Count the first place votes for each candidate, just as you would in the plurality method. If a
Social Choice. CSC304 Lecture 21 November 28, Allan Borodin Adapted from Craig Boutilier s slides
 Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
How Should Members of Parliament (and Presidents) Be Elected? E. Maskin Institute for Advanced Study
 How Should Members of Parliament (and Presidents) Be Elected? E. Maskin Institute for Advanced Study What s wrong with this picture? 2005 U.K. General Election Constituency of Croyden Central vote totals
How Should Members of Parliament (and Presidents) Be Elected? E. Maskin Institute for Advanced Study What s wrong with this picture? 2005 U.K. General Election Constituency of Croyden Central vote totals
Voting: Issues, Problems, and Systems. Voting I 1/31
 Voting: Issues, Problems, and Systems Voting I 1/31 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people do not realize that there
Voting: Issues, Problems, and Systems Voting I 1/31 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people do not realize that there
Voting System: elections
 Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
CS 886: Multiagent Systems. Fall 2016 Kate Larson
 CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
The Borda Majority Count
 The Borda Majority Count Manzoor Ahmad Zahid Harrie de Swart Department of Philosophy, Tilburg University Box 90153, 5000 LE Tilburg, The Netherlands; Email: {M.A.Zahid, H.C.M.deSwart}@uvt.nl Abstract
The Borda Majority Count Manzoor Ahmad Zahid Harrie de Swart Department of Philosophy, Tilburg University Box 90153, 5000 LE Tilburg, The Netherlands; Email: {M.A.Zahid, H.C.M.deSwart}@uvt.nl Abstract
Voting rules: (Dixit and Skeath, ch 14) Recall parkland provision decision:
 rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
Voting Methods
 1.3-1.5 Voting Methods Some announcements Homework #1: Text (pages 28-33) 1, 4, 7, 10, 12, 19, 22, 29, 32, 38, 42, 50, 51, 56-60, 61, 65 (this is posted on Sakai) Math Center study sessions with Katie
1.3-1.5 Voting Methods Some announcements Homework #1: Text (pages 28-33) 1, 4, 7, 10, 12, 19, 22, 29, 32, 38, 42, 50, 51, 56-60, 61, 65 (this is posted on Sakai) Math Center study sessions with Katie
Social Choice Theory. Denis Bouyssou CNRS LAMSADE
 A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
Josh Engwer (TTU) Voting Methods 15 July / 49
 Voting Methods Contemporary Math Josh Engwer TTU 15 July 2015 Josh Engwer (TTU) Voting Methods 15 July 2015 1 / 49 Introduction In free societies, citizens vote for politicians whose values & opinions
Voting Methods Contemporary Math Josh Engwer TTU 15 July 2015 Josh Engwer (TTU) Voting Methods 15 July 2015 1 / 49 Introduction In free societies, citizens vote for politicians whose values & opinions
Math for Liberal Arts MAT 110: Chapter 12 Notes
 Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
Democratic Rules in Context
 Democratic Rules in Context Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Institutions in Context 2012 (PCRC, Turku) Democratic Rules in Context 4 June,
Democratic Rules in Context Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Institutions in Context 2012 (PCRC, Turku) Democratic Rules in Context 4 June,
What is the Best Election Method?
 What is the Best Election Method? E. Maskin Harvard University Gorman Lectures University College, London February 2016 Today and tomorrow will explore 2 Today and tomorrow will explore election methods
What is the Best Election Method? E. Maskin Harvard University Gorman Lectures University College, London February 2016 Today and tomorrow will explore 2 Today and tomorrow will explore election methods
Voting: Issues, Problems, and Systems, Continued. Voting II 1/27
 Voting: Issues, Problems, and Systems, Continued Voting II 1/27 Last Time Last time we discussed some elections and some issues with plurality voting. We started to discuss another voting system, the Borda
Voting: Issues, Problems, and Systems, Continued Voting II 1/27 Last Time Last time we discussed some elections and some issues with plurality voting. We started to discuss another voting system, the Borda
Economics 470 Some Notes on Simple Alternatives to Majority Rule
 Economics 470 Some Notes on Simple Alternatives to Majority Rule Some of the voting procedures considered here are not considered as a means of revealing preferences on a public good issue, but as a means
Economics 470 Some Notes on Simple Alternatives to Majority Rule Some of the voting procedures considered here are not considered as a means of revealing preferences on a public good issue, but as a means
Topics on the Border of Economics and Computation December 18, Lecture 8
 Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
Constructing voting paradoxes with logic and symmetry
 Constructing voting paradoxes with logic and symmetry Part I: Voting and Logic Problem 1. There was a kingdom once ruled by a king and a council of three members: Ana, Bob and Cory. It was a very democratic
Constructing voting paradoxes with logic and symmetry Part I: Voting and Logic Problem 1. There was a kingdom once ruled by a king and a council of three members: Ana, Bob and Cory. It was a very democratic
Problems with Group Decision Making
 Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
The Impossibilities of Voting
 The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
Voting Systems. High School Circle I. June 4, 2017
 Voting Systems High School Circle I June 4, 2017 Today we are going to start our study of voting systems. Put loosely, a voting system takes the preferences of many people, and converted them into a group
Voting Systems High School Circle I June 4, 2017 Today we are going to start our study of voting systems. Put loosely, a voting system takes the preferences of many people, and converted them into a group
In Elections, Irrelevant Alternatives Provide Relevant Data
 1 In Elections, Irrelevant Alternatives Provide Relevant Data Richard B. Darlington Cornell University Abstract The electoral criterion of independence of irrelevant alternatives (IIA) states that a voting
1 In Elections, Irrelevant Alternatives Provide Relevant Data Richard B. Darlington Cornell University Abstract The electoral criterion of independence of irrelevant alternatives (IIA) states that a voting
Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate.
 Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
In deciding upon a winner, there is always one main goal: to reflect the preferences of the people in the most fair way possible.
 Voting Theory 35 Voting Theory In many decision making situations, it is necessary to gather the group consensus. This happens when a group of friends decides which movie to watch, when a company decides
Voting Theory 35 Voting Theory In many decision making situations, it is necessary to gather the group consensus. This happens when a group of friends decides which movie to watch, when a company decides
Voting Protocols. Introduction. Social choice: preference aggregation Our settings. Voting protocols are examples of social choice mechanisms
 Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
An Introduction to Voting Theory
 An Introduction to Voting Theory Zajj Daugherty Adviser: Professor Michael Orrison December 29, 2004 Voting is something with which our society is very familiar. We vote in political elections on which
An Introduction to Voting Theory Zajj Daugherty Adviser: Professor Michael Orrison December 29, 2004 Voting is something with which our society is very familiar. We vote in political elections on which
Voting: Issues, Problems, and Systems
 Voting: Issues, Problems, and Systems 3 March 2014 Voting I 3 March 2014 1/27 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people
Voting: Issues, Problems, and Systems 3 March 2014 Voting I 3 March 2014 1/27 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people
Presidential Election Democrat Grover Cleveland versus Benjamin Harrison. ************************************ Difference of 100,456
 Presidential Election 1886 Democrat Grover Cleveland versus Benjamin Harrison Cleveland 5,540,309 Harrison 5,439,853 ************************************ Difference of 100,456 Electoral College Cleveland
Presidential Election 1886 Democrat Grover Cleveland versus Benjamin Harrison Cleveland 5,540,309 Harrison 5,439,853 ************************************ Difference of 100,456 Electoral College Cleveland
Voting. Hannu Nurmi. Game Theory and Models of Voting. Public Choice Research Centre and Department of Political Science University of Turku
 Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Game Theory and Models of points the history of voting procedures is highly discontinuous, early contributions
Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Game Theory and Models of points the history of voting procedures is highly discontinuous, early contributions
Notes for Session 7 Basic Voting Theory and Arrow s Theorem
 Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
1 Voting In praise of democracy?
 1 Voting In praise of democracy? Many forms of Government have been tried, and will be tried in this world of sin and woe. No one pretends that democracy is perfect or all-wise. Indeed, it has been said
1 Voting In praise of democracy? Many forms of Government have been tried, and will be tried in this world of sin and woe. No one pretends that democracy is perfect or all-wise. Indeed, it has been said
Problems with Group Decision Making
 Problems with Group Decision Making There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Problems with Group Decision Making There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
The Arrow Impossibility Theorem: Where Do We Go From Here?
 The Arrow Impossibility Theorem: Where Do We Go From Here? Eric Maskin Institute for Advanced Study, Princeton Arrow Lecture Columbia University December 11, 2009 I thank Amartya Sen and Joseph Stiglitz
The Arrow Impossibility Theorem: Where Do We Go From Here? Eric Maskin Institute for Advanced Study, Princeton Arrow Lecture Columbia University December 11, 2009 I thank Amartya Sen and Joseph Stiglitz
Voting and preference aggregation
 Voting and preference aggregation CSC304 Lecture 20 November 23, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading
Voting and preference aggregation CSC304 Lecture 20 November 23, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading
Voting and preference aggregation
 Voting and preference aggregation CSC200 Lecture 38 March 14, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading for
Voting and preference aggregation CSC200 Lecture 38 March 14, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading for
: It is mathematically impossible for a democratic voting method to satisfy all of the fairness criteria was proven in 1949.
 Chapter 1 Notes from Voting Theory: the mathematics of the intricacies and subtleties of how voting is done and the votes are counted. In the early 20 th century, social scientists and mathematicians working
Chapter 1 Notes from Voting Theory: the mathematics of the intricacies and subtleties of how voting is done and the votes are counted. In the early 20 th century, social scientists and mathematicians working
Algorithms, Games, and Networks February 7, Lecture 8
 Algorithms, Games, and Networks February 7, 2013 Lecturer: Ariel Procaccia Lecture 8 Scribe: Dong Bae Jun 1 Overview In this lecture, we discuss the topic of social choice by exploring voting rules, axioms,
Algorithms, Games, and Networks February 7, 2013 Lecturer: Ariel Procaccia Lecture 8 Scribe: Dong Bae Jun 1 Overview In this lecture, we discuss the topic of social choice by exploring voting rules, axioms,
Lecture 16: Voting systems
 Lecture 16: Voting systems Economics 336 Economics 336 (Toronto) Lecture 16: Voting systems 1 / 18 Introduction Last lecture we looked at the basic theory of majority voting: instability in voting: Condorcet
Lecture 16: Voting systems Economics 336 Economics 336 (Toronto) Lecture 16: Voting systems 1 / 18 Introduction Last lecture we looked at the basic theory of majority voting: instability in voting: Condorcet
CSC304 Lecture 16. Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting. CSC304 - Nisarg Shah 1
 CSC304 Lecture 16 Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting CSC304 - Nisarg Shah 1 Announcements Assignment 2 was due today at 3pm If you have grace credits left (check MarkUs),
CSC304 Lecture 16 Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting CSC304 - Nisarg Shah 1 Announcements Assignment 2 was due today at 3pm If you have grace credits left (check MarkUs),
Voting and Markov Processes
 Voting and Markov Processes Andrew Nicholson Department of Mathematics The University of North Carolina at Asheville One University Heights Asheville, NC 884. USA Faculty Advisor: Dr. Sam Kaplan Abstract
Voting and Markov Processes Andrew Nicholson Department of Mathematics The University of North Carolina at Asheville One University Heights Asheville, NC 884. USA Faculty Advisor: Dr. Sam Kaplan Abstract
Section 3: The Borda Count Method. Example 4: Using the preference schedule from Example 3, identify the Borda candidate.
 Chapter 1: The Mathematics of Voting Section 3: The Borda Count Method Thursday, January 19, 2012 The Borda Count Method In an election using the Borda Count Method, the candidate with the most points
Chapter 1: The Mathematics of Voting Section 3: The Borda Count Method Thursday, January 19, 2012 The Borda Count Method In an election using the Borda Count Method, the candidate with the most points
