Problems with Group Decision Making
|
|
|
- Leo Bruce
- 5 years ago
- Views:
Transcription
1 Problems with Group Decision Making
2 There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2. Deontological ethics evaluate actions, policies, or institutions in light of the rights, duties, or obligations of the individuals involved.
3 Many people like democracy because they believe it to be a fair way to make decisions. One commonsense notion of fairness is that group decisions should reflect the preferences of the majority of group members. Most people probably agree that a fair way to decide between two options is to choose the option that is preferred by the most people. At its heart, democracy is a system in which the majority rules.
4 An actor is rational if she possesses a complete and transitive preference ordering over a set of outcomes.
5 An actor has a complete preference ordering if she can compare each pair of elements (call them x and y) in a set of outcomes in one of the following ways - either the actor prefers x to y, y to x, or she is indifferent between them. An actor has a transitive preference ordering if for any x, y, and z in the set of outcomes, it is the case that if x is weakly preferred to y, and y is weakly preferred to z, then it must be the case that x is weakly preferred to z.
6 Condorcet s paradox illustrates that a group composed of individuals with rational preferences does not necessarily have rational preferences as a collectivity. Individual rationality is not sufficient to ensure group rationality.
7 Imagine a city council made up of three individuals that must decide whether to: 1. Increase social services (I) 2. Decrease social services (D) 3. Maintain current levels of services (C)
8
9 Let s suppose that the council employs majority rule to make its group decision. One possibility is a round-robin tournament. A round-robin tournament pits each competing alternative against every other alternative an equal number of times in a series of pair-wise votes.
10 The group can t decide! Each alternative wins one round.
11 A group of rational individuals is incapable of making a rational decision for the group as a whole. There is no majority to speak of a different majority supports the winning alternative or outcome in each round.
12
13 Our example demonstrates how a set of rational individuals can form a group with intransitive preferences. In the real world, though, we see deliberative bodies make decisions all the time and they do not appear to be stuck in an endless cycle. Why?
14 There are two broad reasons for this: 1. Preference orderings. 2. Decision-making rules.
15 The councillors having a particular set of preference orderings. Suppose the right-wing councillor s preferences are now a mirror image of the left-wing councillor s. His preferences are now D > C > I instead of D > I > C.
16 If the right-wing councillor s preferences are D > C > I, then C is a Condorcet winner. An option is a Condorcet winner if it beats all of the other options in a series of pair-wise contests.
17 Majority rule is not necessarily incompatible with rational group preferences. Condorcet s Paradox only shows that it is possible for a group of individuals with transitive preferences to produce a group that behaves as if it has intransitive preferences.
18 How often are individuals likely to hold preferences that cause intransitivity?
19
20 In general, we cannot rely on majority rule to produce a coherent sense of what the group wants, especially if there are no institutional mechanisms for keeping the number of voters small or weeding out some of the alternatives.
21 Many political decisions involve bargaining and hence an infinite number of alternatives!
22 Condorcet s Paradox indicates that restricting group decision making to sets of rational individuals is no guarantee that the group as a whole will exhibit rational tendencies. Group intransitivity is unlikely when the set of feasible options is small, but it is almost certain when the set of feasible alternatives gets large. As a result, it is impossible to say that the majority decides except in very restricted circumstances.
23 The analytical insight from Condorcet s Paradox suggests that group intransitivity should be common. But we observe a surprising amount of stability in group decision making in the real world.
24 Perhaps this has something to do with the decision-making rules that we use. 1. The Borda count. 2. A powerful agenda setter.
25 The Borda count asks individuals to rank potential alternatives from their most to least preferred and then assign points to reflect this ranking. The alternative with the most points wins.
26 Using the same preferences as before, the Borda count does not provide a clear winner either.
27 A more troubling aspect of this decision rule can be seen if we consider the introduction of a fourth alternative, future cuts (F C).
28 The Borda count now produces a clear winner! The choice has been influenced by the introduction of what might be called an irrelevant alternative.
29 Decision rules that are not independent of irrelevant alternatives allow wily politicians to more easily manipulate the outcome of a decision making process to produce their most preferred outcome. Rather than making persuasive arguments about the desirability of his most preferred outcome, a politician might get her way by the imaginative introduction of an alternative that has no chance of winning, but that can influence the alternative that is ultimately chosen.
30 Agenda Setting An alternative decision-making mechanism that overcomes the potential instability of majority rule in round-robin tournaments requires actors to begin by considering only a subset of the available pair-wise alternatives.
31 A voting agenda is a plan that determines the order in which votes occur. First round: I vs. D. Second round: Winner of first round vs. C.
32 The agenda setter can get her most preferred outcome. The agenda setter is a dictator!
33 But should we expect all the councillors to vote sincerely? A strategic or sophisticated vote is a vote in which an individual votes in favor of a less preferred option because she believes doing so will ultimately produce a more preferred outcome. A sincere vote is a vote for an individual s most preferred option.
34 Agenda 1: I vs. D, with winner against C. The councillors know that the second round will involve either D vs. C (C wins) or I vs. C (I wins). Thus, the councillors know that if D wins the first round, then the outcome will be C, and that if I wins the first round, then the outcome will be I. This means that the first round of voting is really a contest between C and I (even if they are voting on I and D).
35 Put yourself in the shoes of the right-wing councillor, D > I > C. If she votes for her preferred option (D) in the first round, she will end up with C (her worst preferred option) as the final outcome. Thus, she has a strong incentive to vote strategically for I in the first round, since this will lead to I (her second preferred option) as the final outcome. Some analysts find strategic voting lamentable and prefer decision rules that induce sincere voting.
36 It is possible to avoid the potential for group intransitivity by imposing an agenda.
37 Unfortunately, the outcome of such a process is extremely sensitive to the agenda chosen, and, consequently, either of two things is likely to happen: 1. The instability of group decision making shifts from votes on outcomes to votes on the agendas expected to produce those outcomes. 2. Some subset of actors is given power to control the agenda and, therefore, considerable influence over the outcome likely to be produced.
38 Another way in which stable outcomes might be produced is by placing restrictions on the preferences actors might have. It is possible to convey an individual s preference ordering in terms of a utility function. A utility function is essentially a numerical scaling in which higher numbers stand for higher positions in an individual s preference ordering.
39 A single-peaked preference ordering is characterized by a utility function that reaches a maximum at some point and slopes away from this maximum on either side, such that a movement away from the maximum never raises the actor s utility.
40 The centrist councillor has single-peaked preferences.
41 The right-wing councillor did not have single-peaked preferences.
42 The median voter theorem states that the ideal point of the median voter will win against any alternative in a pair-wise majority-rule election if (i) the number of voters is odd, (ii) voter preferences are single-peaked, (iii) voter preferences are arrayed along a single-issue dimension, (iv) and voters vote sincerely.
43 When voters are arrayed along a single-policy dimension in terms of their ideal points, the median voter is the individual who has at least half of all the voters at his position or to his right and at least half of all the voters at his position or to his left.
44 C wins.
45 Any proposals will converge on the position of the median voter, i.e. C.
46 The MVT shows that the difficulties we encountered with Condorcet s Paradox can be avoided if we are willing to both rule certain preference orderings out of bounds and reduce the policy space to a single dimension.
47 Unfortunately, neither of these restrictions is uncontroversial. There is nothing intrinsically troubling about individual preferences that are not single-peaked. Many political questions are inherently multi-dimensional.
48 Unfortunately, neither of these restrictions is uncontroversial. There is nothing intrinsically troubling about individual preferences that are not single-peaked. Many political questions are inherently multi-dimensional. What if we increase the number of dimensions?
49 Labor, capital, and agriculture are deciding how to divide a pot of subsidies from the government s budget. Each constituency only cares about maximizing subsidies to its own constituency. The decision-making situation can be represented by a two-dimensional policy space.
50
51 An indifference curve is a set of points such that an individual is indifferent between any two points in the set. The winset of some alternative z is the set of alternatives that will defeat z in a pair-wise contest if everyone votes sincerely according to whatever voting rules are being used.
52
53
54
55 The Chaos Theorem states that if there are two or more issue dimensions and three or more voters with preferences in the issue space who all vote sincerely, then except in the case of a rare distribution of ideal points, there will be no Condorcet winner.
56 Unless we are lucky enough to have a set of actors who hold preferences that do not lead to cyclical majorities, then either of two things will happen: 1. The decision-making process will be indeterminate and policy outcomes hopelessly unstable. 2. There will exist an actor the agenda setter with the power to determine the order of votes in such a way that she can produce her most favored outcome.
57 Summary So Far Condorcet s Paradox shows that a set of rational individuals can form a group that is incapable of choosing rationally in round-robin tournaments.
58 Alternative voting schemes like the Borda count allow clear winners in some cases, but the outcomes are not necessarily robust.
59 If we employ single elimination tournaments that form a voting agenda, the cyclical majorities may be avoided but whoever controls the agenda can dictate the outcome.
60 The problem of instability can be overcome if we have a single-issue dimension and each voter has single-peaked preferences.
61 But why should we restrict people s preferences and what about multi-dimensional problems?
62 So, should we just drop majority rule?
63 Arrow s Theorem states that every decision-making process that we could possible design must sacrifice at least one of Arrow s fairness conditions non-dictatorship, universal admissibility, unanimity, or independence from irrelevant alternatives if it is to guarantee group transitivity and, hence, stable outcomes.
64 Arrow presented four fairness conditions that he believed all decision-making processes should meet.
65 1. The non-dictatorship condition states that there must be no individual who fully determines the outcome of the group decision-making process in disregard of the preferences of the other group members.
66 2. The universal admissibility condition states that individuals can adopt any rational preference ordering over the available alternatives.
67 3. The unanimity or pareto optimality condition states that if all individuals in a group prefer x to y, then the group preferences must reflect a preference for x to y as well. Basically, the unanimity condition states that if everybody prefers x to y, the group should not choose y if x is available.
68 4. The independence of irrelevant alternatives condition states that group choice should be unperturbed by changes in the rankings of irrelevant alternatives. Suppose that, when confronted with a choice between x, y, and z, a group prefers x to y. The IIA condition states that if one individual alters their ranking of z, then the group must still prefer x to y.
69 If we take Arrow s conditions of unanimity and IIA as uncontroversial, then we face an institutional trilemma between stable outcomes, universal admissibility, and non-dictatorship.
70 Arrow s Theorem basically states that when designing institutions, we can choose one and only one side of the triangle. If we want group rationality and stable outcomes, then we must give up either non-dictatorship or universal admissibility. If we want to avoid dictatorship, then we must give up group rationality or universal admissibility. If we hold individual preferences inviolable, then we must give up non-dictatorship or group rationality.
71 Arrow s Theorem shows that it is difficult to interpret the outcome of any group decision-making process as necessarily reflecting the will of the group.
72 When a group comes to a clear decision, it may mean that individual preferences lined up in a way that allowed for a clear outcome that represented the desires of a large portion of the group. But it may also mean that individuals with inconvenient preferences were excluded from the process, or that some actor exercised agenda control. In such cases, outcomes may reflect the interest of some powerful subset of the group rather than the preferences of the group as a whole, or even some majority of the group.
73 Every decision-making mechanism must grapple with the trade-offs posed by Arrow s Theorem, and every system of government represents a collection of such decision-making mechanisms. Thus, we can evaluate different systems of government in terms of how their decision-making mechanisms tend to resolve the trade-offs between group rationality and Arrow s fairness criteria. There is no perfect set of decision-making institutions.
74 A piece of legislation cannot cover all conceivable contingencies for which it might be relevant. This requires that in any specific instance a judge, bureaucrat, or lawyer must determine whether a specific statute is applicable or not. Judges often ask, What did Congress intend in passing this law?
75 Liberals (in the American sense) have developed principles of statutory interpretation to enable broad meaning to be read into acts of Congress. Conservatives, on the other hand, insist on requiring judges to stick to the plain meaning of the statutory language.
76 But who is right?
77 But who is right? Short of appealing to our own prejudices and policy preferences, we can provide an analytical perspective based on Arrow s Theorem.
78 Arrow s Theorem cautions against assigning individual properties to groups. Individuals are rational, but a group is not. If this is true, how can one make reference to the intent of a group? Legislators may have an intention, but a legislature does not. Because groups differ from individuals and may be incoherent, legislative intent is an oxymoron!
79 The Daily Show and Social Choice Theory here
Problems with Group Decision Making
 Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Notes for Session 7 Basic Voting Theory and Arrow s Theorem
 Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Chapter 4: Voting and Social Choice.
 Chapter 4: Voting and Social Choice. Topics: Ordinal Welfarism Condorcet and Borda: 2 alternatives for majority voting Voting over Resource Allocation Single-Peaked Preferences Intermediate Preferences
Chapter 4: Voting and Social Choice. Topics: Ordinal Welfarism Condorcet and Borda: 2 alternatives for majority voting Voting over Resource Allocation Single-Peaked Preferences Intermediate Preferences
Public Choice. Slide 1
 Public Choice We investigate how people can come up with a group decision mechanism. Several aspects of our economy can not be handled by the competitive market. Whenever there is market failure, there
Public Choice We investigate how people can come up with a group decision mechanism. Several aspects of our economy can not be handled by the competitive market. Whenever there is market failure, there
Lecture 11. Voting. Outline
 Lecture 11 Voting Outline Hanging Chads Again Did Ralph Nader cause the Bush presidency? A Paradox Left Middle Right 40 25 35 Robespierre Danton Lafarge D L R L R D A Paradox Consider Robespierre versus
Lecture 11 Voting Outline Hanging Chads Again Did Ralph Nader cause the Bush presidency? A Paradox Left Middle Right 40 25 35 Robespierre Danton Lafarge D L R L R D A Paradox Consider Robespierre versus
Elections with Only 2 Alternatives
 Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Chapter 10. The Manipulability of Voting Systems. For All Practical Purposes: Effective Teaching. Chapter Briefing
 Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
answers to some of the sample exercises : Public Choice
 answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
Voting rules: (Dixit and Skeath, ch 14) Recall parkland provision decision:
 rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
Intro Prefs & Voting Electoral comp. Voter Turnout Agency GIP SIP Rent seeking Partisans. Political Economics. Dr. Marc Gronwald Dr.
 Political Economics Dr. Marc Gronwald Dr. Silke Uebelmesser Ludwig-Maximilians University Munich Summer term 2010 Motivation Total government spending as fraction of GDP in the late 1990s: Sweden: 60%;
Political Economics Dr. Marc Gronwald Dr. Silke Uebelmesser Ludwig-Maximilians University Munich Summer term 2010 Motivation Total government spending as fraction of GDP in the late 1990s: Sweden: 60%;
The Problem with Majority Rule. Shepsle and Bonchek Chapter 4
 The Problem with Majority Rule Shepsle and Bonchek Chapter 4 Majority Rule is problematic 1. Who s the majority? 2. Sometimes there is no decisive winner Condorcet s paradox: A group composed of individuals
The Problem with Majority Rule Shepsle and Bonchek Chapter 4 Majority Rule is problematic 1. Who s the majority? 2. Sometimes there is no decisive winner Condorcet s paradox: A group composed of individuals
Election Theory. How voters and parties behave strategically in democratic systems. Mark Crowley
 How voters and parties behave strategically in democratic systems Department of Computer Science University of British Columbia January 30, 2006 Sources Voting Theory Jeff Gill and Jason Gainous. "Why
How voters and parties behave strategically in democratic systems Department of Computer Science University of British Columbia January 30, 2006 Sources Voting Theory Jeff Gill and Jason Gainous. "Why
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory
 MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
CS 886: Multiagent Systems. Fall 2016 Kate Larson
 CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
Social Choice Theory. Denis Bouyssou CNRS LAMSADE
 A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
Chapter 1 Practice Test Questions
 0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
Lecture 16: Voting systems
 Lecture 16: Voting systems Economics 336 Economics 336 (Toronto) Lecture 16: Voting systems 1 / 18 Introduction Last lecture we looked at the basic theory of majority voting: instability in voting: Condorcet
Lecture 16: Voting systems Economics 336 Economics 336 (Toronto) Lecture 16: Voting systems 1 / 18 Introduction Last lecture we looked at the basic theory of majority voting: instability in voting: Condorcet
The Manipulability of Voting Systems. Check off these skills when you feel that you have mastered them.
 Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
Arrow s Impossibility Theorem
 Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
Homework 7 Answers PS 30 November 2013
 Homework 7 Answers PS 30 November 2013 1. Say that there are three people and five candidates {a, b, c, d, e}. Say person 1 s order of preference (from best to worst) is c, b, e, d, a. Person 2 s order
Homework 7 Answers PS 30 November 2013 1. Say that there are three people and five candidates {a, b, c, d, e}. Say person 1 s order of preference (from best to worst) is c, b, e, d, a. Person 2 s order
Mathematics and Social Choice Theory. Topic 4 Voting methods with more than 2 alternatives. 4.1 Social choice procedures
 Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Social Choice: The Impossible Dream. Check off these skills when you feel that you have mastered them.
 Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
Voting Criteria April
 Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
(67686) Mathematical Foundations of AI June 18, Lecture 6
 (67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
(67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
Voting. Suppose that the outcome is determined by the mean of all voter s positions.
 Voting Suppose that the voters are voting on a single-dimensional issue. (Say 0 is extreme left and 100 is extreme right for example.) Each voter has a favorite point on the spectrum and the closer the
Voting Suppose that the voters are voting on a single-dimensional issue. (Say 0 is extreme left and 100 is extreme right for example.) Each voter has a favorite point on the spectrum and the closer the
Answers to Practice Problems. Median voter theorem, supermajority rule, & bicameralism.
 Answers to Practice Problems Median voter theorem, supermajority rule, & bicameralism. Median Voter Theorem Questions: 2.1-2.4, and 2.8. Located at the end of Hinich and Munger, chapter 2, The Spatial
Answers to Practice Problems Median voter theorem, supermajority rule, & bicameralism. Median Voter Theorem Questions: 2.1-2.4, and 2.8. Located at the end of Hinich and Munger, chapter 2, The Spatial
Introduction to Social Choice
 for to Social Choice University of Waterloo January 14, 2013 Outline for 1 2 3 4 for 5 What Is Social Choice Theory for Study of decision problems in which a group has to make the decision The decision
for to Social Choice University of Waterloo January 14, 2013 Outline for 1 2 3 4 for 5 What Is Social Choice Theory for Study of decision problems in which a group has to make the decision The decision
1.6 Arrow s Impossibility Theorem
 1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
Social Choice & Mechanism Design
 Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
Game Theory. Jiang, Bo ( 江波 )
 Game Theory Jiang, Bo ( 江波 ) Jiang.bo@mail.shufe.edu.cn Mechanism Design in Voting Majority voting Three candidates: x, y, z. Three voters: a, b, c. Voter a: x>y>z; voter b: y>z>x; voter c: z>x>y What
Game Theory Jiang, Bo ( 江波 ) Jiang.bo@mail.shufe.edu.cn Mechanism Design in Voting Majority voting Three candidates: x, y, z. Three voters: a, b, c. Voter a: x>y>z; voter b: y>z>x; voter c: z>x>y What
1 Voting In praise of democracy?
 1 Voting In praise of democracy? Many forms of Government have been tried, and will be tried in this world of sin and woe. No one pretends that democracy is perfect or all-wise. Indeed, it has been said
1 Voting In praise of democracy? Many forms of Government have been tried, and will be tried in this world of sin and woe. No one pretends that democracy is perfect or all-wise. Indeed, it has been said
Desirable properties of social choice procedures. We now outline a number of properties that are desirable for these social choice procedures:
 Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Measuring Fairness. Paul Koester () MA 111, Voting Theory September 7, / 25
 Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Public Choice : (c) Single Peaked Preferences and the Median Voter Theorem
 Public Choice : (c) Single Peaked Preferences and the Median Voter Theorem The problem with pairwise majority rule as a choice mechanism, is that it does not always produce a winner. What is meant by a
Public Choice : (c) Single Peaked Preferences and the Median Voter Theorem The problem with pairwise majority rule as a choice mechanism, is that it does not always produce a winner. What is meant by a
First Principle Black s Median Voter Theorem (S&B definition):
 The Unidimensional Spatial Model First Principle Black s Median Voter Theorem (S&B definition): If members of a group have single-peaked preferences, then the ideal point of the median voter has an empty
The Unidimensional Spatial Model First Principle Black s Median Voter Theorem (S&B definition): If members of a group have single-peaked preferences, then the ideal point of the median voter has an empty
Electing the President. Chapter 12 Mathematical Modeling
 Electing the President Chapter 12 Mathematical Modeling Phases of the Election 1. State Primaries seeking nomination how to position the candidate to gather momentum in a set of contests 2. Conventions
Electing the President Chapter 12 Mathematical Modeling Phases of the Election 1. State Primaries seeking nomination how to position the candidate to gather momentum in a set of contests 2. Conventions
Math Circle Voting Methods Practice. March 31, 2013
 Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
Introduction to the Theory of Voting
 November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
VOTING ON INCOME REDISTRIBUTION: HOW A LITTLE BIT OF ALTRUISM CREATES TRANSITIVITY DONALD WITTMAN ECONOMICS DEPARTMENT UNIVERSITY OF CALIFORNIA
 1 VOTING ON INCOME REDISTRIBUTION: HOW A LITTLE BIT OF ALTRUISM CREATES TRANSITIVITY DONALD WITTMAN ECONOMICS DEPARTMENT UNIVERSITY OF CALIFORNIA SANTA CRUZ wittman@ucsc.edu ABSTRACT We consider an election
1 VOTING ON INCOME REDISTRIBUTION: HOW A LITTLE BIT OF ALTRUISM CREATES TRANSITIVITY DONALD WITTMAN ECONOMICS DEPARTMENT UNIVERSITY OF CALIFORNIA SANTA CRUZ wittman@ucsc.edu ABSTRACT We consider an election
Rationality & Social Choice. Dougherty, POLS 8000
 Rationality & Social Choice Dougherty, POLS 8000 Social Choice A. Background 1. Social Choice examines how to aggregate individual preferences fairly. a. Voting is an example. b. Think of yourself writing
Rationality & Social Choice Dougherty, POLS 8000 Social Choice A. Background 1. Social Choice examines how to aggregate individual preferences fairly. a. Voting is an example. b. Think of yourself writing
Arrow s Impossibility Theorem on Social Choice Systems
 Arrow s Impossibility Theorem on Social Choice Systems Ashvin A. Swaminathan January 11, 2013 Abstract Social choice theory is a field that concerns methods of aggregating individual interests to determine
Arrow s Impossibility Theorem on Social Choice Systems Ashvin A. Swaminathan January 11, 2013 Abstract Social choice theory is a field that concerns methods of aggregating individual interests to determine
Head-to-Head Winner. To decide if a Head-to-Head winner exists: Every candidate is matched on a one-on-one basis with every other candidate.
 Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
Introduction to Theory of Voting. Chapter 2 of Computational Social Choice by William Zwicker
 Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Voting Criteria: Majority Criterion Condorcet Criterion Monotonicity Criterion Independence of Irrelevant Alternatives Criterion
 We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
Main idea: Voting systems matter.
 Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
Mathematical Thinking. Chapter 9 Voting Systems
 Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
SOCIAL CHOICES (Voting Methods) THE PROBLEM. Social Choice and Voting. Terminologies
 SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
Fairness Criteria. Review: Election Methods
 Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
MATH 1340 Mathematics & Politics
 MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
Voting Systems That Combine Approval and Preference
 Voting Systems That Combine Approval and Preference Steven J. Brams Department of Politics New York University New York, NY 10003 USA steven.brams@nyu.edu M. Remzi Sanver Department of Economics Istanbul
Voting Systems That Combine Approval and Preference Steven J. Brams Department of Politics New York University New York, NY 10003 USA steven.brams@nyu.edu M. Remzi Sanver Department of Economics Istanbul
Recall: Properties of ranking rules. Recall: Properties of ranking rules. Kenneth Arrow. Recall: Properties of ranking rules. Strategically vulnerable
 Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Electing the President. Chapter 17 Mathematical Modeling
 Electing the President Chapter 17 Mathematical Modeling What do these events have in common? 1824 John Quincy Adams defeats Andrew Jackson 1876 Rutherford B. Hayes defeats Samuel Tilden 1888 Benjamin Harrison
Electing the President Chapter 17 Mathematical Modeling What do these events have in common? 1824 John Quincy Adams defeats Andrew Jackson 1876 Rutherford B. Hayes defeats Samuel Tilden 1888 Benjamin Harrison
9.3 Other Voting Systems for Three or More Candidates
 9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
The mathematics of voting, power, and sharing Part 1
 The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
Web Chapter 3 Political Economy
 Web Chapter 3 Political Economy Chapter Outline W3. W3. W3. W3. 1. Conflict of Interest and Political Economy Do governments and politicians follow their citizens' and constituencies' wishes? 2. Does Democracy
Web Chapter 3 Political Economy Chapter Outline W3. W3. W3. W3. 1. Conflict of Interest and Political Economy Do governments and politicians follow their citizens' and constituencies' wishes? 2. Does Democracy
The Impossibilities of Voting
 The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
Fairness Criteria. Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election.
 Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
POSITIVE POLITICAL THEORY
 POSITIVE POITICA THEORY SOME IMPORTANT THEOREMS AME THEORY IN POITICA SCIENCE Mirror mirror on the wall which is the fairest of them all????? alatasaray Fenerbahce Besiktas Turkcell Telsim Aria DSP DP
POSITIVE POITICA THEORY SOME IMPORTANT THEOREMS AME THEORY IN POITICA SCIENCE Mirror mirror on the wall which is the fairest of them all????? alatasaray Fenerbahce Besiktas Turkcell Telsim Aria DSP DP
Voting Paradoxes and Group Coherence
 William V. Gehrlein Dominique Lepelley Voting Paradoxes and Group Coherence The Condorcet Efficiency of Voting Rules 4y Springer Contents 1 Voting Paradoxes and Their Probabilities 1 1.1 Introduction 1
William V. Gehrlein Dominique Lepelley Voting Paradoxes and Group Coherence The Condorcet Efficiency of Voting Rules 4y Springer Contents 1 Voting Paradoxes and Their Probabilities 1 1.1 Introduction 1
Exercises For DATA AND DECISIONS. Part I Voting
 Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
How should we count the votes?
 How should we count the votes? Bruce P. Conrad January 16, 2008 Were the Iowa caucuses undemocratic? Many politicians, pundits, and reporters thought so in the weeks leading up to the January 3, 2008 event.
How should we count the votes? Bruce P. Conrad January 16, 2008 Were the Iowa caucuses undemocratic? Many politicians, pundits, and reporters thought so in the weeks leading up to the January 3, 2008 event.
Chapter 9: Social Choice: The Impossible Dream
 Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
History of Social Choice and Welfare Economics
 What is Social Choice Theory? History of Social Choice and Welfare Economics SCT concerned with evaluation of alternative methods of collective decision making and logical foundations of welfare economics
What is Social Choice Theory? History of Social Choice and Welfare Economics SCT concerned with evaluation of alternative methods of collective decision making and logical foundations of welfare economics
Sincere versus sophisticated voting when legislators vote sequentially
 Soc Choice Welf (2013) 40:745 751 DOI 10.1007/s00355-011-0639-x ORIGINAL PAPER Sincere versus sophisticated voting when legislators vote sequentially Tim Groseclose Jeffrey Milyo Received: 27 August 2010
Soc Choice Welf (2013) 40:745 751 DOI 10.1007/s00355-011-0639-x ORIGINAL PAPER Sincere versus sophisticated voting when legislators vote sequentially Tim Groseclose Jeffrey Milyo Received: 27 August 2010
Voting System: elections
 Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
CSC304 Lecture 16. Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting. CSC304 - Nisarg Shah 1
 CSC304 Lecture 16 Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting CSC304 - Nisarg Shah 1 Announcements Assignment 2 was due today at 3pm If you have grace credits left (check MarkUs),
CSC304 Lecture 16 Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting CSC304 - Nisarg Shah 1 Announcements Assignment 2 was due today at 3pm If you have grace credits left (check MarkUs),
Sincere Versus Sophisticated Voting When Legislators Vote Sequentially
 Sincere Versus Sophisticated Voting When Legislators Vote Sequentially Tim Groseclose Departments of Political Science and Economics UCLA Jeffrey Milyo Department of Economics University of Missouri September
Sincere Versus Sophisticated Voting When Legislators Vote Sequentially Tim Groseclose Departments of Political Science and Economics UCLA Jeffrey Milyo Department of Economics University of Missouri September
Median voter theorem - continuous choice
 Median voter theorem - continuous choice In most economic applications voters are asked to make a non-discrete choice - e.g. choosing taxes. In these applications the condition of single-peakedness is
Median voter theorem - continuous choice In most economic applications voters are asked to make a non-discrete choice - e.g. choosing taxes. In these applications the condition of single-peakedness is
Voting Protocols. Introduction. Social choice: preference aggregation Our settings. Voting protocols are examples of social choice mechanisms
 Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
The search for a perfect voting system. MATH 105: Contemporary Mathematics. University of Louisville. October 31, 2017
 The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
Computational Social Choice: Spring 2007
 Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Social Choice. CSC304 Lecture 21 November 28, Allan Borodin Adapted from Craig Boutilier s slides
 Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Approaches to Voting Systems
 Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
Voter Sovereignty and Election Outcomes
 Voter Sovereignty and Election Outcomes Steven J. Brams Department of Politics New York University New York, NY 10003 USA steven.brams@nyu.edu M. Remzi Sanver Department of Economics Istanbul Bilgi University
Voter Sovereignty and Election Outcomes Steven J. Brams Department of Politics New York University New York, NY 10003 USA steven.brams@nyu.edu M. Remzi Sanver Department of Economics Istanbul Bilgi University
Political Economics Handout. The Political Economics of Redistributive Policies. Vincenzo Galasso
 Political Economics Handout The Political Economics of Redistributive Policies Vincenzo Galasso 2 Index. Introduction to Political Economics pag. 4.. The Political Economics Approach.2. Political Institutions.3.
Political Economics Handout The Political Economics of Redistributive Policies Vincenzo Galasso 2 Index. Introduction to Political Economics pag. 4.. The Political Economics Approach.2. Political Institutions.3.
Introduction to International Relations Lecture 5: Domestic Politics and Social Choice
 Introduction to International Relations Lecture 5: Domestic Politics and Social Choice Professor Branislav L. Slantchev Department of Political Science, University of California San Diego April 19, 2005
Introduction to International Relations Lecture 5: Domestic Politics and Social Choice Professor Branislav L. Slantchev Department of Political Science, University of California San Diego April 19, 2005
The Borda Majority Count
 The Borda Majority Count Manzoor Ahmad Zahid Harrie de Swart Department of Philosophy, Tilburg University Box 90153, 5000 LE Tilburg, The Netherlands; Email: {M.A.Zahid, H.C.M.deSwart}@uvt.nl Abstract
The Borda Majority Count Manzoor Ahmad Zahid Harrie de Swart Department of Philosophy, Tilburg University Box 90153, 5000 LE Tilburg, The Netherlands; Email: {M.A.Zahid, H.C.M.deSwart}@uvt.nl Abstract
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections
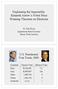 Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
1 Electoral Competition under Certainty
 1 Electoral Competition under Certainty We begin with models of electoral competition. This chapter explores electoral competition when voting behavior is deterministic; the following chapter considers
1 Electoral Competition under Certainty We begin with models of electoral competition. This chapter explores electoral competition when voting behavior is deterministic; the following chapter considers
The Borda count in n-dimensional issue space*
 Public Choice 59:167-176 (1988) Kluwer Academic Publishers The Borda count in n-dimensional issue space* SCOTT L. FELD Department of Sociology, State University of ew York, at Stony Brook BERARD GROFMA
Public Choice 59:167-176 (1988) Kluwer Academic Publishers The Borda count in n-dimensional issue space* SCOTT L. FELD Department of Sociology, State University of ew York, at Stony Brook BERARD GROFMA
Many Social Choice Rules
 Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
How Should Members of Parliament (and Presidents) Be Elected? E. Maskin Institute for Advanced Study
 How Should Members of Parliament (and Presidents) Be Elected? E. Maskin Institute for Advanced Study What s wrong with this picture? 2005 U.K. General Election Constituency of Croyden Central vote totals
How Should Members of Parliament (and Presidents) Be Elected? E. Maskin Institute for Advanced Study What s wrong with this picture? 2005 U.K. General Election Constituency of Croyden Central vote totals
Voting Systems. High School Circle I. June 4, 2017
 Voting Systems High School Circle I June 4, 2017 Today we are going to start our study of voting systems. Put loosely, a voting system takes the preferences of many people, and converted them into a group
Voting Systems High School Circle I June 4, 2017 Today we are going to start our study of voting systems. Put loosely, a voting system takes the preferences of many people, and converted them into a group
What is the Best Election Method?
 What is the Best Election Method? E. Maskin Harvard University Gorman Lectures University College, London February 2016 Today and tomorrow will explore 2 Today and tomorrow will explore election methods
What is the Best Election Method? E. Maskin Harvard University Gorman Lectures University College, London February 2016 Today and tomorrow will explore 2 Today and tomorrow will explore election methods
Make the Math Club Great Again! The Mathematics of Democratic Voting
 Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
c M. J. Wooldridge, used by permission/updated by Simon Parsons, Spring
 Today LECTURE 8: MAKING GROUP DECISIONS CIS 716.5, Spring 2010 We continue thinking in the same framework as last lecture: multiagent encounters game-like interactions participants act strategically We
Today LECTURE 8: MAKING GROUP DECISIONS CIS 716.5, Spring 2010 We continue thinking in the same framework as last lecture: multiagent encounters game-like interactions participants act strategically We
Voting: Issues, Problems, and Systems, Continued
 Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
In Elections, Irrelevant Alternatives Provide Relevant Data
 1 In Elections, Irrelevant Alternatives Provide Relevant Data Richard B. Darlington Cornell University Abstract The electoral criterion of independence of irrelevant alternatives (IIA) states that a voting
1 In Elections, Irrelevant Alternatives Provide Relevant Data Richard B. Darlington Cornell University Abstract The electoral criterion of independence of irrelevant alternatives (IIA) states that a voting
Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate.
 Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
1 Aggregating Preferences
 ECON 301: General Equilibrium III (Welfare) 1 Intermediate Microeconomics II, ECON 301 General Equilibrium III: Welfare We are done with the vital concepts of general equilibrium Its power principally
ECON 301: General Equilibrium III (Welfare) 1 Intermediate Microeconomics II, ECON 301 General Equilibrium III: Welfare We are done with the vital concepts of general equilibrium Its power principally
THE MEDIAN VOTER THEOREM (ONE DIMENSION)
 THE MEDIAN VOTER THEOREM (ONE DIMENSION) 1 2 Single Dimensional Spatial Model Alternatives are the set of points on a line Various ideologies on a spectrum Spending on different programs etc. Single-peaked
THE MEDIAN VOTER THEOREM (ONE DIMENSION) 1 2 Single Dimensional Spatial Model Alternatives are the set of points on a line Various ideologies on a spectrum Spending on different programs etc. Single-peaked
Social choice theory
 Social choice theory A brief introduction Denis Bouyssou CNRS LAMSADE Paris, France Introduction Motivation Aims analyze a number of properties of electoral systems present a few elements of the classical
Social choice theory A brief introduction Denis Bouyssou CNRS LAMSADE Paris, France Introduction Motivation Aims analyze a number of properties of electoral systems present a few elements of the classical
Voting Definitions and Theorems Spring Dr. Martin Montgomery Office: POT 761
 Voting Definitions and Theorems Spring 2014 Dr. Martin Montgomery Office: POT 761 http://www.ms.uky.edu/~martinm/m111 Voting Method: Plurality Definition (The Plurality Method of Voting) For each ballot,
Voting Definitions and Theorems Spring 2014 Dr. Martin Montgomery Office: POT 761 http://www.ms.uky.edu/~martinm/m111 Voting Method: Plurality Definition (The Plurality Method of Voting) For each ballot,
MASSACHUSETTS INSTITUTE OF TECHNOLOGY
 LIBRARY OF THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY Digitized by the Internet Archive in 2011 with funding from Boston Library Consortium IVIember Libraries http://www.archive.org/details/votingforpublicaoomask
LIBRARY OF THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY Digitized by the Internet Archive in 2011 with funding from Boston Library Consortium IVIember Libraries http://www.archive.org/details/votingforpublicaoomask
Political Economics II Spring Lectures 4-5 Part II Partisan Politics and Political Agency. Torsten Persson, IIES
 Lectures 4-5_190213.pdf Political Economics II Spring 2019 Lectures 4-5 Part II Partisan Politics and Political Agency Torsten Persson, IIES 1 Introduction: Partisan Politics Aims continue exploring policy
Lectures 4-5_190213.pdf Political Economics II Spring 2019 Lectures 4-5 Part II Partisan Politics and Political Agency Torsten Persson, IIES 1 Introduction: Partisan Politics Aims continue exploring policy
Democratic Rules in Context
 Democratic Rules in Context Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Institutions in Context 2012 (PCRC, Turku) Democratic Rules in Context 4 June,
Democratic Rules in Context Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Institutions in Context 2012 (PCRC, Turku) Democratic Rules in Context 4 June,
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
Lecture 12: Topics in Voting Theory
 Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
Is Majority Rule the Best Voting Method? Partha Dasgupta and Eric Maskin
 Is Majority Rule the Best Voting Method? by Partha Dasgupta and Eric Maskin June 2003 The authors are, respectively, the Frank Ramsey Professor of Economics at the University of Cambridge, UK, and the
Is Majority Rule the Best Voting Method? by Partha Dasgupta and Eric Maskin June 2003 The authors are, respectively, the Frank Ramsey Professor of Economics at the University of Cambridge, UK, and the
