An Introduction to Voting Theory
|
|
|
- Godfrey Gibbs
- 5 years ago
- Views:
Transcription
1 An Introduction to Voting Theory Zajj Daugherty Adviser: Professor Michael Orrison December 29, 2004 Voting is something with which our society is very familiar. We vote in political elections on which candidates we prefer for mayor, senator, or president. We vote in committees on what actions we want our group to take. It is also a process in which we essentially take part each day. We vote when we go out with our friends and need to decide which restaurant to go to or which movie to see. Voting takes place whenever a group needs to pool preferences to make an overall decision. Unfortunately, it is not always easy to make a single choice when given the preferences of many voters. There are many different methods of voting and tallying votes. In national presidential elections, we choose our top candidate and give no more information. This is called a plurality voting scheme. But there are also situations in which voters might be asked to give a full ranking of a number of alternatives, such as in a marketing survey. If we then chose to give a number of points to these items according to where they are placed in the ranking, this would be positional voting. Each positional scheme is accompanied by a weighting vector, w, whose entries correspond to how many points are given to a voter s first, second,..., last choice. For simplicity, we will often normalize these vectors so that their 1
2 entries range from 1 to 0, with non-increasing values. For example, in the case of plurality voting, w plurality = [1, 0,..., 0]. We will also talk later about the Borda count, which gives a linearly decreasing number of points to a voter s preferences in order. In other words, the weighting vector for the Borda count is w Borda = [1, n 2 n 1, n 3 n 1,..., 0]. Alternatively, we could compare these items pairwise, and give points according to how many times a candidate beats each other candidate. In other words, candidate A wins over candidate B if A is ranked higher than B more times than B is ranked higher than A. There is also approval voting, which was introduced by the Venetians in the 13 th century [6]. In this system, voters simply give out a point to each candidate of which they approve. This leads to the question, however, of which method is the best which method most accurately represents the intention of the voters? Although many methods of voting had been introduced for centuries prior, this debate made its way significantly into academia in the 18 th century. The mathematician and philosopher Marie Jean Antoine Nicolas de Caritat Condorcet brought the pairwise method, first recorded by Ramon Llull of Spain in the 13 th century, back under scrutiny [6]. In 1785, Condorcet published the paper Essai sur l application de l analyse la probabilite des decisions rendues la pluralite des voix (Essay on the Application of Analysis to the Probability of Majority Decisions) [2]. In this paper, he proposed the idea that if a candidate would win all head-to-head comparisons, then that candidate should win the overall election. He recognized, however, that this method would not guarantee a winner. He also discussed what has become known as the Condorcet paradox that in head-to-head comparisons, a society can prefer candidate A over candidate B, candidate B over candidate 2
3 C, and candidate C over candidate A. In other words, the societal preferences in pairwise tallies may not be transitive. Because of his influence in bringing pairwise voting into focus, this method is also often referred to as the Condorcet method. This paper spurred a debate between Condorcet and another French mathematician by the name of Jean Charles de Borda. Borda was known for his work on engineering in the military, and his contributions to developing the metric system. He worked with Condorcet, alongside Laplace, Lavoisier and Legendre, on the Commission of Weights and Measures (founded in 1790) [7]. Borda challenged Condorcet and Llull s method on the grounds that it was not entirely workable. Often, Condorcet s method will show cyclic preferences, and radically fail to produce a winner. Instead, Borda proposed a method developed by Nicholas of Cusa in the 15 th century. He proposed the positional tally for n candidates which gives n points to a voter s top choice, n 1 points to the second choice, and so on (as mentioned previously, we will normalize these values for our purposes). This method was also prone to producing ties, but was more likely to produce a winner. These two mathematicians continued to debate which of these methods was the most fair and productive almost until Condorcet s arrest and death in 1794 [5]. Unfortunately, since their debate was mostly philosophical (despite some use of certain axiomatic and probabilistic tools), and since both systems had strengths and weaknesses, they were not able to make much headway. To illustrate how these two tallying methods differ, let s look at an example. Let s say that we ask voters to rank three candidates A, B, and C. To represent A beating B, we will write A > B (sometimes we will simply write AB). Suppose 18 voters choose the following rankings: 3
4 votes ranking votes ranking votes ranking 2 A > B > C 2 B > A > C 1 C > A > B 5 A > C > B 4 B > C > A 4 C > B > A We would then collect this data in to a profile, p, which represents how many people voted for each ranking of candidates. The profile for this outcome, if we order the rankings alphabetically, is p = (2, 5, 2, 4, 1, 4). If we chose to use the Borda Count to tally these votes, the outcome will give 10.5, 9, and 8.5 points to A, B, and C respectively, giving an over-all ranking of A > B > C. However, if we chose to calculate the pairwise ranking, we will find the following tally: points pair points pair 8 A > B 10 B > A 8 A > C 10 C > A 8 B > C 10 C > B which gives a transitive ranking of C > B > A. You will notice that these two methods of tallying entirely contradict each other in this case. This is what is referred to as a paradox because we calculated differing outcomes using two seemingly fair tallying methods. Following Condorcet and Borda s debate, many people attempted to modify these procedures to improve upon them. For example, in 1876, mathematician Charles Ludwidge Dodgson (better known as Lewis Carroll) proposed a procedure in which a Condorcet winner will be chosen; if there is no Condorcet winner, then the candidate who needs fewest ballots to be changed to become the Condorcet winner will be chosen. John Kemeny proposed a similar system in 1959, where the winner is the candidate who requires the fewest number of rank pairs being exchanged (flipped) on voters 4
5 ballots to make that candidate win by Condorcet s rule. In 1958, Duncan Black constructed a method that blended Condorcet s and Borda s methods. Namely, the Black winner will be the Condorcet winner, unless one fails to exist otherwise, the Borda winner will be chosen. Each of these theories provided additional strengths to Condorcet methods (i.e. we are more likely to calculate a winner), but many of them also resulted in new paradoxes and weaknesses (e.g. the resulting winner may no longer be intuitive) [8]. Another major advance in voting theory was made in the mid-20 th century by the Nobel laureate economist Kenneth Arrow. With contributions from Blau and Murakami, he used axiomatic methods to prove that there can not exist an entirely fair voting system. More specifically, he chose four criteria, and showed that they were inconsistent. These four criteria were Universality, Independence of Irrelevant Alternatives, Citizen s Sovereignty, and Non-dictatorship [4]. Universality (or unrestricted domain) means that the election procedure should provide a full ranking (with strict preferences) for all possible sets of data. Independence of Irrelevant Alternatives requires that any ranking of a subset of alternatives will be unaffected by changes in rankings of other alternatives. Citizen s Sovereignty (or non-imposition) requires that the election procedure allows for all possible outcomes. Nondictatorship simply means that more than one person s vote can affect the outcome. Arrow proved that if the first three criteria were true for a given election procedure, then it must be a dictatorship. This was a profound message for voting theorists, because it meant that we could not possibly construct a truly fair system. Thus, we cannot ask the question how can we construct a fair system. Instead, we can only attempt to decide which system is the most fair. In the late 20 th century, mathematician Donald Saari began to tackle this 5
6 question using geometric methods. In departing from axiomatic methods, he began addressing voting structures as vector spaces. As mentioned before, we can discuss profiles and positional weightings as vectors. We can then naturally begin to study the vector spaces in which these vectors reside. This is precisely what Saari did. He decomposed profile spaces using geometric ideas in order to explain how paradoxes arise, and with what significance. By analyzing the size of various components, he could make statements as to how often certain tally methods would agree with others. Specifically, he has written quite a bit on comparing Condorcet and Borda methods. In three major papers ([10, 11, 12]), Saari devided profile spaces into four subspaces: the kernel (the all ties space, generated by the all-ones vector), the Basic space (containing profiles for which the Borda and Condorcet tallies agree), the Condorcet space (containing profiles which only affect Condorcet outcomes), and the Reversal space (containing profiles which only affect Borda Count outcomes). One major accomplishment he has made is to offer bases for each of these spaces, which allows one to construct a profile with various kinds of conflicts or paradoxes by selecting portions of each subspace. He also showed that the positional tallying method which agrees most with pairwise tallies for full rankings is the Borda count. He has also made some steps in deciphering what happens in cases where candidates drop out of the race. One possible natural extension on this work would be to attempt similar decompositions using algebraic techniques. Abstract algebra lends itself well to both working with the vector spaces of profiles, as well as with maps associated with them. In particular, we can describe various rankings of candidates as permutations elements of the symmetric group. Tallying these profiles can be described as mapping their profile vectors from one space to 6
7 another. One can show that these maps are CS n -module homomorphisms. So in particular, representation theory could prove to be quite useful. Representation theory can then help us to study the profile space in terms of the maps we use to tally the votes. Another, perhaps more natural, extension is to move from studying fully ranked data to studying partially ranked data. It is not always entirely practical to ask for a fully ranked list from voters (for just ten candidates, this would give voters 3, 620, 800 choices!). A Partial ranking calls for voters to place candidates into ranked sets. For example, we might ask voters to tell us, out of six candidates, their top choice, then their next two favorite, and then their three least favorite, without making any distinctions within these categories. Representation theory can help to analyze these objects as well. A significant amount of representation theory has been developed for objects that we can use to prepresent paritally ranked data [15]. Thus, these tools from algebra may prove quite useful for making generalization to this kind of data. 7
8 References [1] J. Borda. Mémoire sur les élections au scrutin. Histoire de l Académie Royale des Sciences, Paris, Historical reference A paper written by Borda in response to Condorect, advocating a specific positional voting shceme. [2] M. Marquis de Condorcet. Essai sur l application de l analyse à la probabilité des décisions rendues à la pluralité des voix. Paris, Historical reference A paper by Condorcet on pairwise voting that spurred the debate between Borda and himself. [3] David S. Dummit and Richard M. Foote. Abstract Algebra. Upper Saddle River, N.J., Prentice Hall, Algebra textbook. [4] Lewis Lum and David J. Kurtz. Voting made easy: A mathematical theory of election procedures, A quick guide to Arrow s theorem. [5] J. J. O Connor and E. F. Robertson. Turnbull www server: Marie jean antoine nicolas de caritat condorcet, Found at history/mathematicians/ Condorcet.html. The Turnbull Server is a good quick reference to historical information on mathematics and mathematicians. [6] J. J. O Connor and E. F. Robertson. Turnbull www server: The history of voting, Found at history/histtopics/voting.html. [7] J. J. O Connor and E. F. Robertson. Turnbull www server: Jean charles de borda, Found at uk/ history/mathematicians/borda.html. [8] Thomas C. Ratliff. A comparison of Dodgson s method and the Borda count. Econom. Theory, 20(2): , This paper takes a similar geometric approach to that of Saari, but compares Borda to a modification of Condorcet s method. In particular, it points out that more problems may arrise when we seemingly improve upon tallying methods in one way or another. [9] Donald G. Saari. Symmetry, voting, and social choice. Math. Intelligencer, 10(3):32 42, This article is a colloquial introduction to Saari s approach to voting theory. It contains many good examples of 8
9 various kinds of paradoxes that arise from different methods of tallying votes. [10] Donald G. Saari. Explaining all three-alternative voting outcomes. J. Econom. Theory, 87(2): , This artical mostly concentrates on decomposing the voting space in the case of 3 candidates. This is a good introductor article to Saari s geometric methods in that it stays in the context of an example to help simplify the ideas. [11] Donald G. Saari. Mathematical structure of voting paradoxes. I. Pairwise votes. Econom. Theory, 15(1):1 53, This is the first of two papers which go into depth in compairing pairwise and positional tally methods. They give a thorough description of voting spaces for fully ranked data using geometric methods. [12] Donald G. Saari. Mathematical structure of voting paradoxes. II. Positional voting. Econom. Theory, 15(1):55 102, This is the second of two major papers on analizing voting methods. See Mathematical structure of voting paradoxes. I. Pairwise votes. [13] Donald G. Saari. Decitions and Elections: Explaining the Unexpected. Cambridge University Press, This book spends extra time building intuition for why our expectations might be as they are. It was written in a similar tone to his article Symmetry, Voting, and Social Choice, in that it is geared for the educated layman. It does, however, also cover Saari s geometric methods. [14] Donald G. Saari and Fabrice Valognes. Geometry, voting, and paradoxes. Math. Mag., 71(4): , This paper is similar to the three outcome paper in that it takes a simple approach to Saari s geometric methods. It is a good introductory paper for getting a grasp on the geometric approach to voting. [15] Bruce Sagan. The Symmetric Group : Representations, Combinatorial Algorithms, and Symmetric Functions. Springer-Verlag New York, Inc., A significant amount of theory for tabloids and irreducible subgroups for partially ranked data can be found here. 9
Desirable properties of social choice procedures. We now outline a number of properties that are desirable for these social choice procedures:
 Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Arrow s Impossibility Theorem
 Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
The Math of Rational Choice - Math 100 Spring 2015
 The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
1.6 Arrow s Impossibility Theorem
 1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
(67686) Mathematical Foundations of AI June 18, Lecture 6
 (67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
(67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
CSC304 Lecture 14. Begin Computational Social Choice: Voting 1: Introduction, Axioms, Rules. CSC304 - Nisarg Shah 1
 CSC304 Lecture 14 Begin Computational Social Choice: Voting 1: Introduction, Axioms, Rules CSC304 - Nisarg Shah 1 Social Choice Theory Mathematical theory for aggregating individual preferences into collective
CSC304 Lecture 14 Begin Computational Social Choice: Voting 1: Introduction, Axioms, Rules CSC304 - Nisarg Shah 1 Social Choice Theory Mathematical theory for aggregating individual preferences into collective
Computational Social Choice: Spring 2007
 Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Recall: Properties of ranking rules. Recall: Properties of ranking rules. Kenneth Arrow. Recall: Properties of ranking rules. Strategically vulnerable
 Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Voting and preference aggregation
 Voting and preference aggregation CSC304 Lecture 20 November 23, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading
Voting and preference aggregation CSC304 Lecture 20 November 23, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading
Voting and Markov Processes
 Voting and Markov Processes Andrew Nicholson Department of Mathematics The University of North Carolina at Asheville One University Heights Asheville, NC 884. USA Faculty Advisor: Dr. Sam Kaplan Abstract
Voting and Markov Processes Andrew Nicholson Department of Mathematics The University of North Carolina at Asheville One University Heights Asheville, NC 884. USA Faculty Advisor: Dr. Sam Kaplan Abstract
Rock the Vote or Vote The Rock
 Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
How should we count the votes?
 How should we count the votes? Bruce P. Conrad January 16, 2008 Were the Iowa caucuses undemocratic? Many politicians, pundits, and reporters thought so in the weeks leading up to the January 3, 2008 event.
How should we count the votes? Bruce P. Conrad January 16, 2008 Were the Iowa caucuses undemocratic? Many politicians, pundits, and reporters thought so in the weeks leading up to the January 3, 2008 event.
Voting and preference aggregation
 Voting and preference aggregation CSC200 Lecture 38 March 14, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading for
Voting and preference aggregation CSC200 Lecture 38 March 14, 2016 Allan Borodin (adapted from Craig Boutilier slides) Announcements and todays agenda Today: Voting and preference aggregation Reading for
Measuring Fairness. Paul Koester () MA 111, Voting Theory September 7, / 25
 Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Reality Math Sam Kaplan, The University of North Carolina at Asheville Dot Sulock, The University of North Carolina at Asheville
 Reality Math Sam Kaplan, The University of North Carolina at Asheville Dot Sulock, The University of North Carolina at Asheville Purpose: Show that the method of voting used can determine the winner. Voting
Reality Math Sam Kaplan, The University of North Carolina at Asheville Dot Sulock, The University of North Carolina at Asheville Purpose: Show that the method of voting used can determine the winner. Voting
Computational Social Choice: Spring 2017
 Computational Social Choice: Spring 2017 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today So far we saw three voting rules: plurality, plurality
Computational Social Choice: Spring 2017 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today So far we saw three voting rules: plurality, plurality
Voting Criteria: Majority Criterion Condorcet Criterion Monotonicity Criterion Independence of Irrelevant Alternatives Criterion
 We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
Fairness Criteria. Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election.
 Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Kybernetika. Robert Bystrický Different approaches to weighted voting systems based on preferential positions
 Kybernetika Robert Bystrický Different approaches to weighted voting systems based on preferential positions Kybernetika, Vol. 48 (2012), No. 3, 536--549 Persistent URL: http://dml.cz/dmlcz/142955 Terms
Kybernetika Robert Bystrický Different approaches to weighted voting systems based on preferential positions Kybernetika, Vol. 48 (2012), No. 3, 536--549 Persistent URL: http://dml.cz/dmlcz/142955 Terms
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Social Choice. CSC304 Lecture 21 November 28, Allan Borodin Adapted from Craig Boutilier s slides
 Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Dictatorships Are Not the Only Option: An Exploration of Voting Theory
 Dictatorships Are Not the Only Option: An Exploration of Voting Theory Geneva Bahrke May 17, 2014 Abstract The field of social choice theory, also known as voting theory, examines the methods by which
Dictatorships Are Not the Only Option: An Exploration of Voting Theory Geneva Bahrke May 17, 2014 Abstract The field of social choice theory, also known as voting theory, examines the methods by which
Democratic Rules in Context
 Democratic Rules in Context Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Institutions in Context 2012 (PCRC, Turku) Democratic Rules in Context 4 June,
Democratic Rules in Context Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Institutions in Context 2012 (PCRC, Turku) Democratic Rules in Context 4 June,
Algorithms, Games, and Networks February 7, Lecture 8
 Algorithms, Games, and Networks February 7, 2013 Lecturer: Ariel Procaccia Lecture 8 Scribe: Dong Bae Jun 1 Overview In this lecture, we discuss the topic of social choice by exploring voting rules, axioms,
Algorithms, Games, and Networks February 7, 2013 Lecturer: Ariel Procaccia Lecture 8 Scribe: Dong Bae Jun 1 Overview In this lecture, we discuss the topic of social choice by exploring voting rules, axioms,
Mathematical Thinking. Chapter 9 Voting Systems
 Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Voting. Hannu Nurmi. Game Theory and Models of Voting. Public Choice Research Centre and Department of Political Science University of Turku
 Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Game Theory and Models of points the history of voting procedures is highly discontinuous, early contributions
Hannu Nurmi Public Choice Research Centre and Department of Political Science University of Turku Game Theory and Models of points the history of voting procedures is highly discontinuous, early contributions
Introduction to Theory of Voting. Chapter 2 of Computational Social Choice by William Zwicker
 Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Constructing voting paradoxes with logic and symmetry Teacher s Notes
 Constructing voting paradoxes with logic and symmetry Teacher s Notes Elena Galaktionova elena@problemtrove.org Mobile Math Circle This is a loose transcript of the Math Circle, with occasional notes on
Constructing voting paradoxes with logic and symmetry Teacher s Notes Elena Galaktionova elena@problemtrove.org Mobile Math Circle This is a loose transcript of the Math Circle, with occasional notes on
Chapter 1 Practice Test Questions
 0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
Trying to please everyone. Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam
 Trying to please everyone Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Classical ILLC themes: Logic, Language, Computation Also interesting: Social Choice Theory In
Trying to please everyone Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Classical ILLC themes: Logic, Language, Computation Also interesting: Social Choice Theory In
The mathematics of voting, power, and sharing Part 1
 The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
1 Voting In praise of democracy?
 1 Voting In praise of democracy? Many forms of Government have been tried, and will be tried in this world of sin and woe. No one pretends that democracy is perfect or all-wise. Indeed, it has been said
1 Voting In praise of democracy? Many forms of Government have been tried, and will be tried in this world of sin and woe. No one pretends that democracy is perfect or all-wise. Indeed, it has been said
The Impossibilities of Voting
 The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
Topics on the Border of Economics and Computation December 18, Lecture 8
 Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
Fairness Criteria. Review: Election Methods
 Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
Math for Liberal Studies
 Math for Liberal Studies As we have discussed, when there are only two candidates in an election, deciding the winner is easy May s Theorem states that majority rule is the best system However, the situation
Math for Liberal Studies As we have discussed, when there are only two candidates in an election, deciding the winner is easy May s Theorem states that majority rule is the best system However, the situation
Chapter 9: Social Choice: The Impossible Dream
 Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
SOCIAL CHOICES (Voting Methods) THE PROBLEM. Social Choice and Voting. Terminologies
 SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
Arrow s Conditions and Approval Voting. Which group-ranking method is best?
 Arrow s Conditions and Approval Voting Which group-ranking method is best? Paradoxes When a group ranking results in an unexpected winner, the situation is known as a paradox. A special type of paradox
Arrow s Conditions and Approval Voting Which group-ranking method is best? Paradoxes When a group ranking results in an unexpected winner, the situation is known as a paradox. A special type of paradox
12.2 Defects in Voting Methods
 12.2 Defects in Voting Methods Recall the different Voting Methods: 1. Plurality - one vote to one candidate, the others get nothing The remaining three use a preference ballot, where all candidates are
12.2 Defects in Voting Methods Recall the different Voting Methods: 1. Plurality - one vote to one candidate, the others get nothing The remaining three use a preference ballot, where all candidates are
CS 886: Multiagent Systems. Fall 2016 Kate Larson
 CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
Exercises For DATA AND DECISIONS. Part I Voting
 Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Math116Chap1VotingPart2.notebook January 12, Part II. Other Methods of Voting and Other "Fairness Criteria"
 Part II Other Methods of Voting and Other "Fairness Criteria" Plurality with Elimination Method Round 1. Count the first place votes for each candidate, just as you would in the plurality method. If a
Part II Other Methods of Voting and Other "Fairness Criteria" Plurality with Elimination Method Round 1. Count the first place votes for each candidate, just as you would in the plurality method. If a
VOTING SYSTEMS AND ARROW S THEOREM
 VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
On removing the Condorcet influence from pairwise elections data
 Economics Working Papers (2002 2016) Economics 7-2-2010 On removing the Condorcet influence from pairwise elections data Abhit Chandra Iowa State University, achandra@iastate.edu Sunanda Roy Iowa State
Economics Working Papers (2002 2016) Economics 7-2-2010 On removing the Condorcet influence from pairwise elections data Abhit Chandra Iowa State University, achandra@iastate.edu Sunanda Roy Iowa State
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory
 MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
Social welfare functions
 Social welfare functions We have defined a social choice function as a procedure that determines for each possible profile (set of preference ballots) of the voters the winner or set of winners for the
Social welfare functions We have defined a social choice function as a procedure that determines for each possible profile (set of preference ballots) of the voters the winner or set of winners for the
Chapter 2 Descriptions of the Voting Methods to Be Analyzed
 Chapter 2 Descriptions of the Voting Methods to Be Analyzed Abstract This chapter describes the 18 most well-known voting procedures for electing one out of several candidates. These procedures are divided
Chapter 2 Descriptions of the Voting Methods to Be Analyzed Abstract This chapter describes the 18 most well-known voting procedures for electing one out of several candidates. These procedures are divided
Voting Methods
 1.3-1.5 Voting Methods Some announcements Homework #1: Text (pages 28-33) 1, 4, 7, 10, 12, 19, 22, 29, 32, 38, 42, 50, 51, 56-60, 61, 65 (this is posted on Sakai) Math Center study sessions with Katie
1.3-1.5 Voting Methods Some announcements Homework #1: Text (pages 28-33) 1, 4, 7, 10, 12, 19, 22, 29, 32, 38, 42, 50, 51, 56-60, 61, 65 (this is posted on Sakai) Math Center study sessions with Katie
Head-to-Head Winner. To decide if a Head-to-Head winner exists: Every candidate is matched on a one-on-one basis with every other candidate.
 Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
Approaches to Voting Systems
 Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
Math for Liberal Arts MAT 110: Chapter 12 Notes
 Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
The Mathematics of Voting
 The Mathematics of Voting Voting Methods Summary Last time, we considered elections for Math Club President from among four candidates: Alisha (A), Boris (B), Carmen (C), and Dave (D). All 37 voters submitted
The Mathematics of Voting Voting Methods Summary Last time, we considered elections for Math Club President from among four candidates: Alisha (A), Boris (B), Carmen (C), and Dave (D). All 37 voters submitted
Voting System: elections
 Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
Josh Engwer (TTU) Voting Methods 15 July / 49
 Voting Methods Contemporary Math Josh Engwer TTU 15 July 2015 Josh Engwer (TTU) Voting Methods 15 July 2015 1 / 49 Introduction In free societies, citizens vote for politicians whose values & opinions
Voting Methods Contemporary Math Josh Engwer TTU 15 July 2015 Josh Engwer (TTU) Voting Methods 15 July 2015 1 / 49 Introduction In free societies, citizens vote for politicians whose values & opinions
The Mathematics of Voting
 Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
9.3 Other Voting Systems for Three or More Candidates
 9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
Arrow s Impossibility Theorem on Social Choice Systems
 Arrow s Impossibility Theorem on Social Choice Systems Ashvin A. Swaminathan January 11, 2013 Abstract Social choice theory is a field that concerns methods of aggregating individual interests to determine
Arrow s Impossibility Theorem on Social Choice Systems Ashvin A. Swaminathan January 11, 2013 Abstract Social choice theory is a field that concerns methods of aggregating individual interests to determine
Introduction to the Theory of Voting
 November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate.
 Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
Elections with Only 2 Alternatives
 Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Many Social Choice Rules
 Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
The Arrow Impossibility Theorem: Where Do We Go From Here?
 The Arrow Impossibility Theorem: Where Do We Go From Here? Eric Maskin Institute for Advanced Study, Princeton Arrow Lecture Columbia University December 11, 2009 I thank Amartya Sen and Joseph Stiglitz
The Arrow Impossibility Theorem: Where Do We Go From Here? Eric Maskin Institute for Advanced Study, Princeton Arrow Lecture Columbia University December 11, 2009 I thank Amartya Sen and Joseph Stiglitz
The Mathematics of Voting. The Mathematics of Voting
 1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
Mathematics and Social Choice Theory. Topic 4 Voting methods with more than 2 alternatives. 4.1 Social choice procedures
 Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections
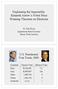 Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Voting rules: (Dixit and Skeath, ch 14) Recall parkland provision decision:
 rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
answers to some of the sample exercises : Public Choice
 answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
Introduction to Social Choice
 for to Social Choice University of Waterloo January 14, 2013 Outline for 1 2 3 4 for 5 What Is Social Choice Theory for Study of decision problems in which a group has to make the decision The decision
for to Social Choice University of Waterloo January 14, 2013 Outline for 1 2 3 4 for 5 What Is Social Choice Theory for Study of decision problems in which a group has to make the decision The decision
Public Choice. Slide 1
 Public Choice We investigate how people can come up with a group decision mechanism. Several aspects of our economy can not be handled by the competitive market. Whenever there is market failure, there
Public Choice We investigate how people can come up with a group decision mechanism. Several aspects of our economy can not be handled by the competitive market. Whenever there is market failure, there
Make the Math Club Great Again! The Mathematics of Democratic Voting
 Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
Make the Math Club Great Again! The Mathematics of Democratic Voting Darci L. Kracht Kent State University Undergraduate Mathematics Club April 14, 2016 How do you become Math Club King, I mean, President?
1.1 The Basic Elements of an Election 1.2 The Plurality Method
 1.1 The Basic Elements of an Election 1.2 The Plurality Method Some announcements Math Center study sessions with Katie Greene (TA). Tuesday and Wednesday 7pm-9pm in Kirby 120. First Math colloquium this
1.1 The Basic Elements of an Election 1.2 The Plurality Method Some announcements Math Center study sessions with Katie Greene (TA). Tuesday and Wednesday 7pm-9pm in Kirby 120. First Math colloquium this
Notes for Session 7 Basic Voting Theory and Arrow s Theorem
 Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Rationality of Voting and Voting Systems: Lecture II
 Rationality of Voting and Voting Systems: Lecture II Rationality of Voting Systems Hannu Nurmi Department of Political Science University of Turku Three Lectures at National Research University Higher
Rationality of Voting and Voting Systems: Lecture II Rationality of Voting Systems Hannu Nurmi Department of Political Science University of Turku Three Lectures at National Research University Higher
Social Choice Theory. Denis Bouyssou CNRS LAMSADE
 A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
Voting Systems. High School Circle I. June 4, 2017
 Voting Systems High School Circle I June 4, 2017 Today we are going to start our study of voting systems. Put loosely, a voting system takes the preferences of many people, and converted them into a group
Voting Systems High School Circle I June 4, 2017 Today we are going to start our study of voting systems. Put loosely, a voting system takes the preferences of many people, and converted them into a group
Voting: Issues, Problems, and Systems, Continued. Voting II 1/27
 Voting: Issues, Problems, and Systems, Continued Voting II 1/27 Last Time Last time we discussed some elections and some issues with plurality voting. We started to discuss another voting system, the Borda
Voting: Issues, Problems, and Systems, Continued Voting II 1/27 Last Time Last time we discussed some elections and some issues with plurality voting. We started to discuss another voting system, the Borda
Constructing voting paradoxes with logic and symmetry
 Constructing voting paradoxes with logic and symmetry Part I: Voting and Logic Problem 1. There was a kingdom once ruled by a king and a council of three members: Ana, Bob and Cory. It was a very democratic
Constructing voting paradoxes with logic and symmetry Part I: Voting and Logic Problem 1. There was a kingdom once ruled by a king and a council of three members: Ana, Bob and Cory. It was a very democratic
Voting: Issues, Problems, and Systems, Continued
 Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
Voting: Issues, Problems, and Systems
 Voting: Issues, Problems, and Systems 3 March 2014 Voting I 3 March 2014 1/27 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people
Voting: Issues, Problems, and Systems 3 March 2014 Voting I 3 March 2014 1/27 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people
Simple methods for single winner elections
 Simple methods for single winner elections Christoph Börgers Mathematics Department Tufts University Medford, MA April 14, 2018 http://emerald.tufts.edu/~cborgers/ I have posted these slides there. 1 /
Simple methods for single winner elections Christoph Börgers Mathematics Department Tufts University Medford, MA April 14, 2018 http://emerald.tufts.edu/~cborgers/ I have posted these slides there. 1 /
Voting: Issues, Problems, and Systems. Voting I 1/36
 Voting: Issues, Problems, and Systems Voting I 1/36 Each even year every member of the house is up for election and about a third of the senate seats are up for grabs. Most people do not realize that there
Voting: Issues, Problems, and Systems Voting I 1/36 Each even year every member of the house is up for election and about a third of the senate seats are up for grabs. Most people do not realize that there
Mathematics of Voting Systems. Tanya Leise Mathematics & Statistics Amherst College
 Mathematics of Voting Systems Tanya Leise Mathematics & Statistics Amherst College Arrow s Impossibility Theorem 1) No special treatment of particular voters or candidates 2) Transitivity A>B and B>C implies
Mathematics of Voting Systems Tanya Leise Mathematics & Statistics Amherst College Arrow s Impossibility Theorem 1) No special treatment of particular voters or candidates 2) Transitivity A>B and B>C implies
Connecting Voting Theory and Graph Theory
 Connecting Voting Theory and Graph Theory Karl-Dieter Crisman Gordon College Willamette University Math Colloquium, October 13, 2016 Karl-Dieter Crisman (Gordon College) Graphs and Voting WU Colloquium
Connecting Voting Theory and Graph Theory Karl-Dieter Crisman Gordon College Willamette University Math Colloquium, October 13, 2016 Karl-Dieter Crisman (Gordon College) Graphs and Voting WU Colloquium
The Reasonableness of Independence:
 The Reasonableness of Independence: A Conversation from Condorcet and Borda to Arrow and Saari by Iain McLean Nuffield College, Oxford OX1 1NF iain.mclean@nuf.ox.ac.uk Nuffield College Politics Working
The Reasonableness of Independence: A Conversation from Condorcet and Borda to Arrow and Saari by Iain McLean Nuffield College, Oxford OX1 1NF iain.mclean@nuf.ox.ac.uk Nuffield College Politics Working
Math Circle Voting Methods Practice. March 31, 2013
 Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
Practice TEST: Chapter 14
 TOPICS Practice TEST: Chapter 14 Name: Period: Date: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use the given information to answer the question.
TOPICS Practice TEST: Chapter 14 Name: Period: Date: SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use the given information to answer the question.
Social Choice Welfare Springer-Verlag 1987
 Soc Choice Welfare (1987) 4:185-206 Social Choice Welfare Springer-Verlag 1987 Independence of Clones as a Criterion for Voting Rules T. N. Tideman* Virginia Polytechnic Institute and State University,
Soc Choice Welfare (1987) 4:185-206 Social Choice Welfare Springer-Verlag 1987 Independence of Clones as a Criterion for Voting Rules T. N. Tideman* Virginia Polytechnic Institute and State University,
VOTING TO ELECT A SINGLE CANDIDATE
 N. R. Miller 05/01/97 5 th rev. 8/22/06 VOTING TO ELECT A SINGLE CANDIDATE This discussion focuses on single-winner elections, in which a single candidate is elected from a field of two or more candidates.
N. R. Miller 05/01/97 5 th rev. 8/22/06 VOTING TO ELECT A SINGLE CANDIDATE This discussion focuses on single-winner elections, in which a single candidate is elected from a field of two or more candidates.
Voting: Issues, Problems, and Systems. Voting I 1/31
 Voting: Issues, Problems, and Systems Voting I 1/31 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people do not realize that there
Voting: Issues, Problems, and Systems Voting I 1/31 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people do not realize that there
Voting Protocols. Introduction. Social choice: preference aggregation Our settings. Voting protocols are examples of social choice mechanisms
 Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
c M. J. Wooldridge, used by permission/updated by Simon Parsons, Spring
 Today LECTURE 8: MAKING GROUP DECISIONS CIS 716.5, Spring 2010 We continue thinking in the same framework as last lecture: multiagent encounters game-like interactions participants act strategically We
Today LECTURE 8: MAKING GROUP DECISIONS CIS 716.5, Spring 2010 We continue thinking in the same framework as last lecture: multiagent encounters game-like interactions participants act strategically We
Voting with Bidirectional Elimination
 Voting with Bidirectional Elimination Matthew S. Cook Economics Department Stanford University March, 2011 Advisor: Jonathan Levin Abstract Two important criteria for judging the quality of a voting algorithm
Voting with Bidirectional Elimination Matthew S. Cook Economics Department Stanford University March, 2011 Advisor: Jonathan Levin Abstract Two important criteria for judging the quality of a voting algorithm
Social choice theory
 Social choice theory A brief introduction Denis Bouyssou CNRS LAMSADE Paris, France Introduction Motivation Aims analyze a number of properties of electoral systems present a few elements of the classical
Social choice theory A brief introduction Denis Bouyssou CNRS LAMSADE Paris, France Introduction Motivation Aims analyze a number of properties of electoral systems present a few elements of the classical
Intro to Contemporary Math
 Intro to Contemporary Math Independence of Irrelevant Alternatives Criteria Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Independence of Irrelevant Alternatives Criteria
Intro to Contemporary Math Independence of Irrelevant Alternatives Criteria Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Independence of Irrelevant Alternatives Criteria
Lecture 12: Topics in Voting Theory
 Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
Lecture 12: Topics in Voting Theory Eric Pacuit ILLC, University of Amsterdam staff.science.uva.nl/ epacuit epacuit@science.uva.nl Lecture Date: May 11, 2006 Caput Logic, Language and Information: Social
The search for a perfect voting system. MATH 105: Contemporary Mathematics. University of Louisville. October 31, 2017
 The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
Main idea: Voting systems matter.
 Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
