Arrow s Impossibility Theorem on Social Choice Systems
|
|
|
- Annabella Gibbs
- 6 years ago
- Views:
Transcription
1 Arrow s Impossibility Theorem on Social Choice Systems Ashvin A. Swaminathan January 11, 2013 Abstract Social choice theory is a field that concerns methods of aggregating individual interests to determine net social preferences. Arrow s Impossibility Theorem states that no social choice system can satisfy all requirements in a collection of reasonable criteria. We make the notion of reasonable voting systems precise by stating the four properties that voting systems must have in order to be reasonable. We then present two different proofs of Arrow s Theorem, both of which combine three of the reasonable properties to obtain a contradiction of the fourth. Finally, we discuss the theorem s implications for social choice theory and show how the theorem can be applied to real-world examples of voting systems. 1. Social Choice Theory Kenneth Arrow s Impossibility Theorem, which he first introduced in his seminal 1951 book Social Choice and Individual Values, is considered to be the mathematical foundation of modern social choice theory, a field that concerns methods of aggregating individual interests to determine net social preferences [1]. The theorem essentially states that no social choice system can determine net social preferences without violating at least one condition in a specific set of reasonable criteria. These criteria have their roots in the democratic basis of social choice theory, the belief that social decisions should, in some reasonable way, depend on the preferences of individuals in the society [4] and on nothing else. As we discuss in Section 2, we can make the notion of reasonable criteria precise by considering a list of properties that we would like our social choice systems to satisfy. The process of social decision-making has numerous real-world applications. The market system itself (assuming laissez-faire, of course) is a prime example of the importance of social choice: in this system, the price and quantity of a certain product is determined solely by the net demand (the choice to buy) of the product s buyers and the net supply (the choice to sell) of the product s sellers. Moreover, on the buyers side itself, individuals makes choices among various products to maximize their own total utility. Likewise, on the sellers side itself, individual firms make choices among various resources to maximize their own total profits. In particular, a firm is owned by its shareholders, so if the shareholders disagree about how profit can be maximized, the wishes of each individual shareholder need to be aggregated in a social choice system to yield the final production strategy (which cannot be done reasonably, according to Arrow s Theorem) [3]. Also, some decisions are made in the government, in which case representatives make decisions on nation-wide issues through some kind of voting system (this is what goes on in governmental bodies like the U.S. Congress all the time). In sum, whether school administrators are seeking to maximize their 1
2 students total utility by selecting appropriate numbers of basketballs and footballs to purchase or citizens are choosing among various candidates for their country s presidency, people are constantly forced to make choices. 2. Voting Systems For ease of discussion, we will consider only voting systems throughout the rest of the paper, but it is important to recognize that our subsequent arguments for voting systems can be easily applied to social choice systems in general. Before we define voting systems precisely, we provide the necessary background definitions and assumptions. Let the finite set S be the set of all voters in society and the finite set C be the set of all candidates (candidates are often more generally referred to as alternatives or options). For any two candidates a, b C, each s S has either a > s b, meaning that s prefers a to b, or the opposite. As is true of economic theory in general, we make the assumption that the voters are rational individuals. Firstly, each rational voter must rank all candidates in a transitive manner, so that for any s S, if a > s b and b > s c, then a > s c must hold. Because each voter s preferences are transitive, we can conclude that in making preferences, rational voters define total orderings upon elements of C. Secondly, rational voters must order their candidates without coercion, so that each voter composes his preferences independently of all other voters. Finally, let O C denote the set of all total orderings of the elements of C. Define a voting system to be any map V : (O C ) S O C that takes some t 1, t 2,..., t S O C to some t O C (here, (O C ) S = O C O C is the set of all possible combinations, or voter profiles, of individual voters orderings). In other words, a voting system V is a function that is given as input the preferences (the t i s) of each voter and that returns as output some ordering, or social ranking, (t) of the candidates. Whether t is reasonable or not is independent of the definition of a voting system; we now consider properties that any reasonable voting system should satisfy along with abbreviations that we will use to refer to them throughout the rest of the paper: 1. Unanimity (U): If for some a, b C we have a > s b for every s S, then t = V (t 1, t 2,..., t S ) is an ordering that satisfies a > b. In other words, the output t of the voting system V, when applied to a society that unanimously prefers a to b, must rank a above b. So, if a society is in consensus about the ranking of a pair of candidates, then the society must choose to rank those two candidates in accordance with their common preference. 2. Rationality (R): The ranking t = V (t 1, t 2,..., t S ) is a total ordering, so that transitivity is obeyed in the social ordering t of the candidates. 3. Non-dictatorship (ND): If for some i 1, 2,..., S and any a, b C we have that whenever t i satisfies a > b and t j satisfies b > a for j i, t = V (t 1, t 2,..., t S ) satisfies a > b, then the voter whose ranking is t i is said to be a dictator. A reasonable voting system should not have any dictators. Thus, the output t of the voting system should not satisfy the wishes of a 2
3 single voter by overriding the wishes of all the other voters. For property ND to make sense, we require monotonicity: if a, b C such that t has a < b, then lowering the relative position of a (with respect to b) in any of the t i should not alter the relative position of a in t. 4. Independence of Irrelevant Alternatives (IIA): For a, b, c C, the ranking between a, b in t should be identical to the corresponding ranking when the position of c in t is changed. That is, if a is ranked higher than b socially, then the position c has in t should be of no relevance whatsoever to the fact that a > b in t. Note that if there are only two candidates, then we get property IIA for free, because we do not have any third alternatives to be concerned about. In fact, as we discuss in Section 4, Arrow s Theorem does not even apply when C = 2; in this case, it is actually possible to have a voting system that satisfies all of the above properties. 3. Arrow s Theorem and its Proofs In this section, we state Arrow s Theorem formally and provide two short proofs, one due to Terence Tao [5] and the other due to John Geanakoplos [2]. Theorem (Arrow s Theorem). If C 3, then the properties U, R, ND, and IIA are inconsistent. We note that both proofs often utilize a, b, c C, thereby employing the assumption in the theorem statement that C Tao s Proof In Tao s original proof of the theorem, it is assumed that there is impartiality among the candidates; i.e., the output of the voting system does not change when the candidates are permuted. Nonetheless, as we show in the following proof, a similar approach can be used to obtain the theorem without the assumption of impartiality among the candidates. Furthermore, Tao s statement of property ND is different from the one presented in Section 2. Specifically, Tao says that a voter who can force his preference for some a, b C is a dictator, while we would only consider that voter to be a dictator over a, b. The following proof thus possesses further modifications needed to make it work with our version of property ND. Tao s proof relies on the notion of a quorum, a set of voters who can force their mutual preference on the social ranking. For some particular pair a, b C, define a quorum to be a set Q of voters such that if the ranking of every q Q satisfies a > q b and if the ranking of every s S \ Q satisfies b > s a, then the output ranking of the voting system satisfies a > b. This means that the members of a quorum for candidates a, b can always force a > b in the social ranking by unanimously ranking a > b in their individual rankings. We denote the set of all quorums of a, b by R(a, b) (a pair of candidates might have multiple possible quorums). Note that by property U, S is a quorum for any two candidates. 3
4 Because of property IIA, whether or not Q R(a, b) can force a > b depends only on the individual rankings of a, b for each q Q. Thus, the notion of a quorum is well-defined; in other words, a quorum cannot force a > b sometimes but fail to force a > b at other times if all its members vote a > b. Notice that each pair of candidates has a distinct notion of quorum, for Q need not be a quorum for some other pair of candidates c, d (i.e., Q R(a, b) does not imply Q R(c, d)) if impartiality exists among the candidates. We are now ready to prove Arrow s Theorem. We first prove that if Q 1 R(a, b) and Q 2 R(b, c), then Q 1 Q 2 R(a, c) for any distinct a, b, c C; that is, the intersection of a quorum for candidates a, b and a quorum for candidates b, c is a quorum for candidates a, c. Suppose that the following are true: 1. All members of Q 1 vote a > b; 2. All members of Q 2 vote b > c; and 3. All members of S \ (Q 1 Q 2 ) vote c > a. Clearly, the social ranking must have a > b and b > c (because Q 1 and Q 2 are quorums), and so, using property R, we obtain a > c. Thus, Q 1 Q 2 is a quorum for a, c, and sticking to our notation, we can write Q 1 Q 2 R(a, c). We next prove that for any s S, we have S \ {s} is a quorum for any two candidates. Suppose that this is not the case. Then s is a dictator for at least one pair a, b C, meaning that s can force his preference between a, b in the social ranking. We claim that S \ {s} must then be a quorum for a, c, where c C satisfies c b. This claim is true because s would otherwise be a dictator for a, c, implying that s must be a dictator for all pairs involving a, b, c. Then, by repeating this argument where a is replaced with each of the other elements of C, we see that s must be a dictator for all pairs of candidates, which violates property ND. Since s R(a, b) and S \ {s} R(a, c), we have {s} (S \ {s}) = R(b, c), a result that clearly violates property U, as the empty set cannot possibly be a quorum. Therefore, for any s S, we have S \ {s} is a quorum for any two candidates. If s 1, s 2,..., s S are all the elements of S and a, b, c are three elements of C (this is where the C 3 condition comes in), then S \ {s 1 } R(a, b), S \ {s i } R(b, c) for all i 1. So, S i=1 (S \ {s i}) = is a quorum (it is either in R(a, b) or R(a, c)), so the empty set is a quorum, which again violates property U. Thus, the properties U, R, ND, and IIA together are inconsistent, and we have the theorem Geanakoplos Proof In [2], Geanakoplos gave two other short proofs of Arrow s Theorem, but in our view, the one presented below is the simplest of the three. While Tao s proof uses the properties R, ND, and IIA to contradict property U, Geanakoplos proof uses the properties U, R, and IIA to contradict property ND. For this proof, we first require 4
5 the statement and proof of the Extremal Lemma. The main body of theorem s proof relies not only on the Extremal Lemma, but also on the notion of an extremely pivotal voter, one who can move a candidate from the very bottom to the very top of a social ranking. Notice that because the set of candidates is finite and because all rankings are total orderings, we can say that the least candidate in a ranking is at the very bottom and that the greatest candidate in a ranking is at the very top. Extremal Lemma. For any b C, if every voter places b at the very top or bottom of his ranking, then the social ranking also has b at the very top or bottom. Proof. Suppose the contrary. Then for some a, c C, we have a > b and b > c in the social ranking, and by property R, a > c must hold. Because b occupies an extremal position in each voter s ranking, we can change the individual rankings of a, c without affecting the position of b in the social ranking. So, we can make each individual ranking satisfy c > a. Now by property U, c > a must hold, which is a contradiction. Thus we have the lemma. We are now ready to prove Arrow s Theorem. Let a voter s S be called extremely pivotal for b C at some voter profile P if s induces the social ranking of a, b to change by altering his own ranking of a, b as long as the rest of the rankings are fixed at their positions in P. We first prove that at some voter profile P and for some b C, we can find s S such that s is extremely pivotal. Let us construct P in such a way that all voters rank b at the very bottom of their individual rankings. By property U, b is clearly at the bottom of the social ranking in this case. Now suppose the voters successively move b from the very bottom to the very top of their rankings, and let s be the first voter who, by moving b from the very bottom to the very top of his ranking, causes the position of b in the social ranking to increase. By the Extremal Lemma, s causes b to move to the very top of the social ranking, meaning that for any candidate a b, s can alter the social ranking of a, b by altering his own ranking of a, b, keeping all other rankings fixed. So, s is extremely pivotal. We next prove that s is a dictator for all pairs a, c C that satisfy a b and c b. Call the voter profile that results just before s moves b from the very bottom to the very top of his own ranking P 1. Just after s moves b from the very bottom to the very top of his own ranking, suppose that no more voters execute this operation, and call the resulting voter profile P 2. Further suppose that s then moves a above b in his own ranking, so that a > s b > s c, and let the rankings of a, c for all voters in S \ {s} be arbitrary, keeping b in its extremal position. Call this new voter profile P 3. By property IIA, we can say that (1) P 3 is identical to P 1 with respect to candidates a, b; and (2) P 3 is identical to P 2 with respect to candidates b, c. Therefore, V (P 3 ) satisfies a > b and b > c, so by R, V (P 3 ) satisfies a > c whenever a > s c, showing that s is a dictator for a, c. We conclude by proving that s is a dictator for all pairs of candidates. To do this, we need only show that s is a dictator for all pairs of candidates involving b, because we have already shown that s is a dictator for all other pairs. Some d S is a dictator for all pairs involving b, because we could have repeated the arguments of the previous two paragraphs using some other candidate a instead 5
6 of b. But because s can change the social ranking of a, b for any a C in moving from profile P 1 to profile P 2, we must have that s = d, so s is a dictator for a, b, thereby violating property ND. Thus we have the theorem. 4. Consequences of Arrow s Theorem Arrow s Theorem unfortunately tells us that voting systems cannot satisfy all reasonable criteria at once. Therefore, all of the standard voting systems used to make decisions today must at times violate at least one of the properties U, R, ND, and IIA. We now consider the pitfalls of two common voting systems, majority rule and plurality rule. Example 4.1. The Marquis de Condorcet, a French mathematician, was the first to study the fairness of majority rule in depth [3]. In the majority rule voting system, the winning candidate must be preferred by a majority to each other candidate. For example, if a, b, c C, suppose a > b > c has 44%, b > c > a has 34%, and c > b > a has 22% of the vote. Then b is the winner of the election since he is ranked higher than a by 56% of the voters and since he is ranked higher than c by 78% of the voters, although a has the most first place votes at 44%. To show that majority rule violates one of the properties U, R, ND, and IIA, let us consider Condorcet s paradox, described as follows. Suppose for a, b, c C the social ranking that 1/3 of the voters rank a > b > c, another 1/3 rank b > c > a, and the last third rank c > a > b. Then a majority prefer a to b, a majority prefer b to c, and a majority prefer a to c, a result that contradicts property R. Note that we do not obtain such paradoxes if C = 2; i.e., there are two candidates. If there is a majority, then the winner is obvious, and if not, then a random selection of the winner will suffice. Example 4.2. Plurality rule is the voting system that is most widely used in the United States [3] today; it is used for electing members of congress, and the election of presidents is similar to a collection of plurality rule systems, one for each state. In the plurality rule voting system, the candidate who is ranked first by most voters is the winner. For example, if a, b, c C, suppose a > b > c has 44%, b > c > a has 34%, and c > b > a has 22% of the vote. Then a is the winner of the election since he has the plurality of 44%. Note that this result is different from the same situation when majority rule was used, as plurality rule gave a as the winner but majority rule gave b as the winner. To show that plurality rule violates one of the properties U, R, ND, and IIA, let us consider the 2000 presidential election in the United States. There were three contestants in the election, Republican George Bush, Democrat Al Gore, and Green Party candidate Ralph Nader. In the case of Florida, which uses plurality rule and was the deciding state, Gore lost to Bush by less than 600 votes [3]. Had Nader not run in the election, it is quite likely that many Green Party supporters would have ended up voting for Gore on account of his more liberal policies. Thus, Gore would have probably taken Florida by storm had Nader, who is known in political terms as a spoiler, not run, a result that violates property IIA because the removal of a supposedly irrelevant candidate would have changed the outcome of the election. 6
7 Gloomy though the theorem may seem, Impossibility Theorem may actually be a misnomer for Arrow s result. While the theorem does state that no voting system satisfies the properties U, R, ND, and IIA, many voting systems actually come quite close to doing so. As we saw in Section 2, majority rule violates property R if the voter profile happens to result in a Condorcet paradox. However, if the situations inducing such paradoxes are rare, then we can exclude those situations, and voting systems like majority rule can actually end up satisfying all four properties [3]. For example, let a, b, c C. If unlikely rankings like, say, a > b > c and b > a > c are excluded, then the only possible rankings left are a > c > b, c > b > a, c > a > b, and b > c > a, no three of which form Condorcet paradoxes. Therefore, majority rule, when taken with an understanding of which outcomes are likely and which are not, can actually be reasonable ; i.e., property R will not be violated, so a winner can be determined. This may very well be why Arrow originally gave his result the optimistic title General Possibility Theorem [4]. Acknowledgements I thank Dr. Daniel Kane of the Stanford University Mathematics Department for enlightening discussions on Arrow s Theorem and for providing valuable feedback on the version of Tao s proof presented in this paper. I also thank Dr. Simon Rubinstein-Salzedo of the Dartmouth College Mathematics Department for his insightful comments on this paper. References [1] Kenneth Arrow. Social Choice and Individual Values. John Wiley and Sons, Inc., [2] John Geanakoplos. Three brief proofs of arrow s impossibility theorem. Cowles Foundation for Research in Economics, Yale University, Paper No. 1116, [3] Eric Maskin. The arrow impossibility theorem: Where do we go from here? Arrow Lecture, Columbia University, [4] Amartya Sen. Arrow and the impossibility theorem. Arrow Lecture, Columbia University, [5] Terence Tao. Arrow s theorem. tao/preprints/misc.html. 7
VOTING SYSTEMS AND ARROW S THEOREM
 VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
VOTING SYSTEMS AND ARROW S THEOREM AKHIL MATHEW Abstract. The following is a brief discussion of Arrow s theorem in economics. I wrote it for an economics class in high school. 1. Background Arrow s theorem
Topics on the Border of Economics and Computation December 18, Lecture 8
 Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
Topics on the Border of Economics and Computation December 18, 2005 Lecturer: Noam Nisan Lecture 8 Scribe: Ofer Dekel 1 Correlated Equilibrium In the previous lecture, we introduced the concept of correlated
The Arrow Impossibility Theorem: Where Do We Go From Here?
 The Arrow Impossibility Theorem: Where Do We Go From Here? Eric Maskin Institute for Advanced Study, Princeton Arrow Lecture Columbia University December 11, 2009 I thank Amartya Sen and Joseph Stiglitz
The Arrow Impossibility Theorem: Where Do We Go From Here? Eric Maskin Institute for Advanced Study, Princeton Arrow Lecture Columbia University December 11, 2009 I thank Amartya Sen and Joseph Stiglitz
Voting Criteria April
 Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Lesson Plan For All Practical Purposes An Introduction to Social Choice Majority Rule and Condorcet s Method Mathematical Literacy in Today s World, 9th ed. Other Voting Systems for Three or More Candidates
Mathematics and Social Choice Theory. Topic 4 Voting methods with more than 2 alternatives. 4.1 Social choice procedures
 Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Mathematics and Social Choice Theory Topic 4 Voting methods with more than 2 alternatives 4.1 Social choice procedures 4.2 Analysis of voting methods 4.3 Arrow s Impossibility Theorem 4.4 Cumulative voting
Chapter 9: Social Choice: The Impossible Dream
 Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
Chapter 9: Social Choice: The Impossible Dream The application of mathematics to the study of human beings their behavior, values, interactions, conflicts, and methods of making decisions is generally
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory
 MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
MATH4999 Capstone Projects in Mathematics and Economics Topic 3 Voting methods and social choice theory 3.1 Social choice procedures Plurality voting Borda count Elimination procedures Sequential pairwise
Arrow s Impossibility Theorem
 Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
Arrow s Impossibility Theorem Some announcements Final reflections due on Monday. You now have all of the methods and so you can begin analyzing the results of your election. Today s Goals We will discuss
1.6 Arrow s Impossibility Theorem
 1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
1.6 Arrow s Impossibility Theorem Some announcements Homework #2: Text (pages 33-35) 51, 56-60, 61, 65, 71-75 (this is posted on Sakai) For Monday, read Chapter 2 (pages 36-57) Today s Goals We will discuss
answers to some of the sample exercises : Public Choice
 answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
answers to some of the sample exercises : Public Choice Ques 1 The following table lists the way that 5 different voters rank five different alternatives. Is there a Condorcet winner under pairwise majority
Recall: Properties of ranking rules. Recall: Properties of ranking rules. Kenneth Arrow. Recall: Properties of ranking rules. Strategically vulnerable
 Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Outline for today Stat155 Game Theory Lecture 26: More Voting. Peter Bartlett December 1, 2016 1 / 31 2 / 31 Recall: Voting and Ranking Recall: Properties of ranking rules Assumptions There is a set Γ
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections
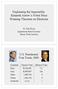 Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Explaining the Impossible: Kenneth Arrow s Nobel Prize Winning Theorem on Elections Dr. Rick Klima Appalachian State University Boone, North Carolina U.S. Presidential Vote Totals, 2000 Candidate Bush
Social welfare functions
 Social welfare functions We have defined a social choice function as a procedure that determines for each possible profile (set of preference ballots) of the voters the winner or set of winners for the
Social welfare functions We have defined a social choice function as a procedure that determines for each possible profile (set of preference ballots) of the voters the winner or set of winners for the
Simple methods for single winner elections
 Simple methods for single winner elections Christoph Börgers Mathematics Department Tufts University Medford, MA April 14, 2018 http://emerald.tufts.edu/~cborgers/ I have posted these slides there. 1 /
Simple methods for single winner elections Christoph Börgers Mathematics Department Tufts University Medford, MA April 14, 2018 http://emerald.tufts.edu/~cborgers/ I have posted these slides there. 1 /
Elections with Only 2 Alternatives
 Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Math 203: Chapter 12: Voting Systems and Drawbacks: How do we decide the best voting system? Elections with Only 2 Alternatives What is an individual preference list? Majority Rules: Pick 1 of 2 candidates
Dictatorships Are Not the Only Option: An Exploration of Voting Theory
 Dictatorships Are Not the Only Option: An Exploration of Voting Theory Geneva Bahrke May 17, 2014 Abstract The field of social choice theory, also known as voting theory, examines the methods by which
Dictatorships Are Not the Only Option: An Exploration of Voting Theory Geneva Bahrke May 17, 2014 Abstract The field of social choice theory, also known as voting theory, examines the methods by which
Math116Chap1VotingPart2.notebook January 12, Part II. Other Methods of Voting and Other "Fairness Criteria"
 Part II Other Methods of Voting and Other "Fairness Criteria" Plurality with Elimination Method Round 1. Count the first place votes for each candidate, just as you would in the plurality method. If a
Part II Other Methods of Voting and Other "Fairness Criteria" Plurality with Elimination Method Round 1. Count the first place votes for each candidate, just as you would in the plurality method. If a
Desirable properties of social choice procedures. We now outline a number of properties that are desirable for these social choice procedures:
 Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
Desirable properties of social choice procedures We now outline a number of properties that are desirable for these social choice procedures: 1. Pareto [named for noted economist Vilfredo Pareto (1848-1923)]
A NOTE ON THE THEORY OF SOCIAL CHOICE
 A NOTE ON THE THEORY OF SOCIAL CHOICE Professor Arrow brings to his treatment of the theory of social welfare (I) a fine unity of mathematical rigour and insight into fundamental issues of social philosophy.
A NOTE ON THE THEORY OF SOCIAL CHOICE Professor Arrow brings to his treatment of the theory of social welfare (I) a fine unity of mathematical rigour and insight into fundamental issues of social philosophy.
Mathematical Thinking. Chapter 9 Voting Systems
 Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Mathematical Thinking Chapter 9 Voting Systems Voting Systems A voting system is a rule for transforming a set of individual preferences into a single group decision. What are the desirable properties
Fairness Criteria. Review: Election Methods
 Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
Review: Election Methods Plurality method: the candidate with a plurality of votes wins. Plurality-with-elimination method (Instant runoff): Eliminate the candidate with the fewest first place votes. Keep
Main idea: Voting systems matter.
 Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
Voting Systems Main idea: Voting systems matter. Electoral College Winner takes all in most states (48/50) (plurality in states) 270/538 electoral votes needed to win (majority) If 270 isn t obtained -
(67686) Mathematical Foundations of AI June 18, Lecture 6
 (67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
(67686) Mathematical Foundations of AI June 18, 2008 Lecturer: Ariel D. Procaccia Lecture 6 Scribe: Ezra Resnick & Ariel Imber 1 Introduction: Social choice theory Thus far in the course, we have dealt
Notes for Session 7 Basic Voting Theory and Arrow s Theorem
 Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Notes for Session 7 Basic Voting Theory and Arrow s Theorem We follow up the Impossibility (Session 6) of pooling expert probabilities, while preserving unanimities in both unconditional and conditional
Social Choice: The Impossible Dream. Check off these skills when you feel that you have mastered them.
 Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
Chapter Objectives Check off these skills when you feel that you have mastered them. Analyze and interpret preference list ballots. Explain three desired properties of Majority Rule. Explain May s theorem.
Fairness Criteria. Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election.
 Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Fairness Criteria Majority Criterion: If a candidate receives a majority of the first place votes, that candidate should win the election. The plurality, plurality-with-elimination, and pairwise comparisons
Voting: Issues, Problems, and Systems, Continued
 Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
Voting: Issues, Problems, and Systems, Continued 7 March 2014 Voting III 7 March 2014 1/27 Last Time We ve discussed several voting systems and conditions which may or may not be satisfied by a system.
Measuring Fairness. Paul Koester () MA 111, Voting Theory September 7, / 25
 Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
Measuring Fairness We ve seen FOUR methods for tallying votes: Plurality Borda Count Pairwise Comparisons Plurality with Elimination Are these methods reasonable? Are these methods fair? Today we study
The search for a perfect voting system. MATH 105: Contemporary Mathematics. University of Louisville. October 31, 2017
 The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
The search for a perfect voting system MATH 105: Contemporary Mathematics University of Louisville October 31, 2017 Review of Fairness Criteria Fairness Criteria 2 / 14 We ve seen three fairness criteria
Voting: Issues, Problems, and Systems. Voting I 1/36
 Voting: Issues, Problems, and Systems Voting I 1/36 Each even year every member of the house is up for election and about a third of the senate seats are up for grabs. Most people do not realize that there
Voting: Issues, Problems, and Systems Voting I 1/36 Each even year every member of the house is up for election and about a third of the senate seats are up for grabs. Most people do not realize that there
Chapter 4: Voting and Social Choice.
 Chapter 4: Voting and Social Choice. Topics: Ordinal Welfarism Condorcet and Borda: 2 alternatives for majority voting Voting over Resource Allocation Single-Peaked Preferences Intermediate Preferences
Chapter 4: Voting and Social Choice. Topics: Ordinal Welfarism Condorcet and Borda: 2 alternatives for majority voting Voting over Resource Allocation Single-Peaked Preferences Intermediate Preferences
CSC304 Lecture 16. Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting. CSC304 - Nisarg Shah 1
 CSC304 Lecture 16 Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting CSC304 - Nisarg Shah 1 Announcements Assignment 2 was due today at 3pm If you have grace credits left (check MarkUs),
CSC304 Lecture 16 Voting 3: Axiomatic, Statistical, and Utilitarian Approaches to Voting CSC304 - Nisarg Shah 1 Announcements Assignment 2 was due today at 3pm If you have grace credits left (check MarkUs),
Computational Social Choice: Spring 2007
 Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Computational Social Choice: Spring 2007 Ulle Endriss Institute for Logic, Language and Computation University of Amsterdam Ulle Endriss 1 Plan for Today This lecture will be an introduction to voting
Voting Protocols. Introduction. Social choice: preference aggregation Our settings. Voting protocols are examples of social choice mechanisms
 Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
Voting Protocols Yiling Chen September 14, 2011 Introduction Social choice: preference aggregation Our settings A set of agents have preferences over a set of alternatives Taking preferences of all agents,
Introduction to the Theory of Voting
 November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
November 11, 2015 1 Introduction What is Voting? Motivation 2 Axioms I Anonymity, Neutrality and Pareto Property Issues 3 Voting Rules I Condorcet Extensions and Scoring Rules 4 Axioms II Reinforcement
Social Choice. CSC304 Lecture 21 November 28, Allan Borodin Adapted from Craig Boutilier s slides
 Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Social Choice CSC304 Lecture 21 November 28, 2016 Allan Borodin Adapted from Craig Boutilier s slides 1 Todays agenda and announcements Today: Review of popular voting rules. Axioms, Manipulation, Impossibility
Social Choice Theory. Denis Bouyssou CNRS LAMSADE
 A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
A brief and An incomplete Introduction Introduction to to Social Choice Theory Denis Bouyssou CNRS LAMSADE What is Social Choice Theory? Aim: study decision problems in which a group has to take a decision
Lecture 11. Voting. Outline
 Lecture 11 Voting Outline Hanging Chads Again Did Ralph Nader cause the Bush presidency? A Paradox Left Middle Right 40 25 35 Robespierre Danton Lafarge D L R L R D A Paradox Consider Robespierre versus
Lecture 11 Voting Outline Hanging Chads Again Did Ralph Nader cause the Bush presidency? A Paradox Left Middle Right 40 25 35 Robespierre Danton Lafarge D L R L R D A Paradox Consider Robespierre versus
Safe Votes, Sincere Votes, and Strategizing
 Safe Votes, Sincere Votes, and Strategizing Rohit Parikh Eric Pacuit April 7, 2005 Abstract: We examine the basic notion of strategizing in the statement of the Gibbard-Satterthwaite theorem and note that
Safe Votes, Sincere Votes, and Strategizing Rohit Parikh Eric Pacuit April 7, 2005 Abstract: We examine the basic notion of strategizing in the statement of the Gibbard-Satterthwaite theorem and note that
What is the Best Election Method?
 What is the Best Election Method? E. Maskin Harvard University Gorman Lectures University College, London February 2016 Today and tomorrow will explore 2 Today and tomorrow will explore election methods
What is the Best Election Method? E. Maskin Harvard University Gorman Lectures University College, London February 2016 Today and tomorrow will explore 2 Today and tomorrow will explore election methods
Voting: Issues, Problems, and Systems. Voting I 1/31
 Voting: Issues, Problems, and Systems Voting I 1/31 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people do not realize that there
Voting: Issues, Problems, and Systems Voting I 1/31 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people do not realize that there
Arrow s Conditions and Approval Voting. Which group-ranking method is best?
 Arrow s Conditions and Approval Voting Which group-ranking method is best? Paradoxes When a group ranking results in an unexpected winner, the situation is known as a paradox. A special type of paradox
Arrow s Conditions and Approval Voting Which group-ranking method is best? Paradoxes When a group ranking results in an unexpected winner, the situation is known as a paradox. A special type of paradox
Problems with Group Decision Making
 Problems with Group Decision Making There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Problems with Group Decision Making There are two ways of evaluating political systems. 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Constructing voting paradoxes with logic and symmetry
 Constructing voting paradoxes with logic and symmetry Part I: Voting and Logic Problem 1. There was a kingdom once ruled by a king and a council of three members: Ana, Bob and Cory. It was a very democratic
Constructing voting paradoxes with logic and symmetry Part I: Voting and Logic Problem 1. There was a kingdom once ruled by a king and a council of three members: Ana, Bob and Cory. It was a very democratic
The mathematics of voting, power, and sharing Part 1
 The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
The mathematics of voting, power, and sharing Part 1 Voting systems A voting system or a voting scheme is a way for a group of people to select one from among several possibilities. If there are only two
Voting Criteria: Majority Criterion Condorcet Criterion Monotonicity Criterion Independence of Irrelevant Alternatives Criterion
 We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
We have discussed: Voting Theory Arrow s Impossibility Theorem Voting Methods: Plurality Borda Count Plurality with Elimination Pairwise Comparisons Voting Criteria: Majority Criterion Condorcet Criterion
Rock the Vote or Vote The Rock
 Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
Rock the Vote or Vote The Rock Tom Edgar Department of Mathematics University of Notre Dame Notre Dame, Indiana October 27, 2008 Graduate Student Seminar Introduction Basic Counting Extended Counting Introduction
Chapter 1 Practice Test Questions
 0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
0728 Finite Math Chapter 1 Practice Test Questions VOCABULARY. On the exam, be prepared to match the correct definition to the following terms: 1) Voting Elements: Single-choice ballot, preference ballot,
Math Circle Voting Methods Practice. March 31, 2013
 Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
Voting Methods Practice 1) Three students are running for class vice president: Chad, Courtney and Gwyn. Each student ranked the candidates in order of preference. The chart below shows the results of
How should we count the votes?
 How should we count the votes? Bruce P. Conrad January 16, 2008 Were the Iowa caucuses undemocratic? Many politicians, pundits, and reporters thought so in the weeks leading up to the January 3, 2008 event.
How should we count the votes? Bruce P. Conrad January 16, 2008 Were the Iowa caucuses undemocratic? Many politicians, pundits, and reporters thought so in the weeks leading up to the January 3, 2008 event.
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Section 15.1 Voting Methods INB Table of Contents Date Topic Page # February 24, 2014 Test #3 Practice Test 38 February 24, 2014 Test #3 Practice Test Workspace 39 March 10, 2014 Test #3 40 March 10, 2014
Chapter 9: Social Choice: The Impossible Dream Lesson Plan
 Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
Lesson Plan For ll Practical Purposes Voting and Social hoice Majority Rule and ondorcet s Method Mathematical Literacy in Today s World, 7th ed. Other Voting Systems for Three or More andidates Plurality
Voting Definitions and Theorems Spring Dr. Martin Montgomery Office: POT 761
 Voting Definitions and Theorems Spring 2014 Dr. Martin Montgomery Office: POT 761 http://www.ms.uky.edu/~martinm/m111 Voting Method: Plurality Definition (The Plurality Method of Voting) For each ballot,
Voting Definitions and Theorems Spring 2014 Dr. Martin Montgomery Office: POT 761 http://www.ms.uky.edu/~martinm/m111 Voting Method: Plurality Definition (The Plurality Method of Voting) For each ballot,
Rationality & Social Choice. Dougherty, POLS 8000
 Rationality & Social Choice Dougherty, POLS 8000 Social Choice A. Background 1. Social Choice examines how to aggregate individual preferences fairly. a. Voting is an example. b. Think of yourself writing
Rationality & Social Choice Dougherty, POLS 8000 Social Choice A. Background 1. Social Choice examines how to aggregate individual preferences fairly. a. Voting is an example. b. Think of yourself writing
Approaches to Voting Systems
 Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
Approaches to Voting Systems Properties, paradoxes, incompatibilities Hannu Nurmi Department of Philosophy, Contemporary History and Political Science University of Turku Game Theory and Voting Systems,
Head-to-Head Winner. To decide if a Head-to-Head winner exists: Every candidate is matched on a one-on-one basis with every other candidate.
 Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
Head-to-Head Winner A candidate is a Head-to-Head winner if he or she beats all other candidates by majority rule when they meet head-to-head (one-on-one). To decide if a Head-to-Head winner exists: Every
PROBLEM SET #2: VOTING RULES
 POLI 309 Fall 2006 due 10/13/06 PROBLEM SET #2: VOTING RULES Write your answers directly on this page. Unless otherwise specified, assume all voters vote sincerely, i.e., in accordance with their preferences.
POLI 309 Fall 2006 due 10/13/06 PROBLEM SET #2: VOTING RULES Write your answers directly on this page. Unless otherwise specified, assume all voters vote sincerely, i.e., in accordance with their preferences.
Math for Liberal Studies
 Math for Liberal Studies As we have discussed, when there are only two candidates in an election, deciding the winner is easy May s Theorem states that majority rule is the best system However, the situation
Math for Liberal Studies As we have discussed, when there are only two candidates in an election, deciding the winner is easy May s Theorem states that majority rule is the best system However, the situation
How Should Members of Parliament (and Presidents) Be Elected? E. Maskin Institute for Advanced Study
 How Should Members of Parliament (and Presidents) Be Elected? E. Maskin Institute for Advanced Study What s wrong with this picture? 2005 U.K. General Election Constituency of Croyden Central vote totals
How Should Members of Parliament (and Presidents) Be Elected? E. Maskin Institute for Advanced Study What s wrong with this picture? 2005 U.K. General Election Constituency of Croyden Central vote totals
Voting: Issues, Problems, and Systems
 Voting: Issues, Problems, and Systems 3 March 2014 Voting I 3 March 2014 1/27 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people
Voting: Issues, Problems, and Systems 3 March 2014 Voting I 3 March 2014 1/27 In 2014 every member of the house is up for election and about a third of the senate seats will be up for grabs. Most people
The Impossibilities of Voting
 The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
The Impossibilities of Voting Introduction Majority Criterion Condorcet Criterion Monotonicity Criterion Irrelevant Alternatives Criterion Arrow s Impossibility Theorem 2012 Pearson Education, Inc. Slide
Font Size: A A. Eric Maskin and Amartya Sen JANUARY 19, 2017 ISSUE. 1 of 7 2/21/ :01 AM
 1 of 7 2/21/2017 10:01 AM Font Size: A A Eric Maskin and Amartya Sen JANUARY 19, 2017 ISSUE Americans have been using essentially the same rules to elect presidents since the beginning of the Republic.
1 of 7 2/21/2017 10:01 AM Font Size: A A Eric Maskin and Amartya Sen JANUARY 19, 2017 ISSUE Americans have been using essentially the same rules to elect presidents since the beginning of the Republic.
The Mathematics of Voting
 Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
Math 165 Winston Salem, NC 28 October 2010 Voting for 2 candidates Today, we talk about voting, which may not seem mathematical. President of the Math TA s Let s say there s an election which has just
Social Choice & Mechanism Design
 Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
Decision Making in Robots and Autonomous Agents Social Choice & Mechanism Design Subramanian Ramamoorthy School of Informatics 2 April, 2013 Introduction Social Choice Our setting: a set of outcomes agents
MATH 1340 Mathematics & Politics
 MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
MATH 1340 Mathematics & Politics Lecture 6 June 29, 2015 Slides prepared by Iian Smythe for MATH 1340, Summer 2015, at Cornell University 1 Basic criteria A social choice function is anonymous if voters
Is Majority Rule the Best Voting Method? Partha Dasgupta and Eric Maskin
 Is Majority Rule the Best Voting Method? by Partha Dasgupta and Eric Maskin June 2003 The authors are, respectively, the Frank Ramsey Professor of Economics at the University of Cambridge, UK, and the
Is Majority Rule the Best Voting Method? by Partha Dasgupta and Eric Maskin June 2003 The authors are, respectively, the Frank Ramsey Professor of Economics at the University of Cambridge, UK, and the
CS 886: Multiagent Systems. Fall 2016 Kate Larson
 CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
CS 886: Multiagent Systems Fall 2016 Kate Larson Multiagent Systems We will study the mathematical and computational foundations of multiagent systems, with a focus on the analysis of systems where agents
Problems with Group Decision Making
 Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
Problems with Group Decision Making There are two ways of evaluating political systems: 1. Consequentialist ethics evaluate actions, policies, or institutions in regard to the outcomes they produce. 2.
c M. J. Wooldridge, used by permission/updated by Simon Parsons, Spring
 Today LECTURE 8: MAKING GROUP DECISIONS CIS 716.5, Spring 2010 We continue thinking in the same framework as last lecture: multiagent encounters game-like interactions participants act strategically We
Today LECTURE 8: MAKING GROUP DECISIONS CIS 716.5, Spring 2010 We continue thinking in the same framework as last lecture: multiagent encounters game-like interactions participants act strategically We
9.3 Other Voting Systems for Three or More Candidates
 9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
9.3 Other Voting Systems for Three or More Candidates With three or more candidates, there are several additional procedures that seem to give reasonable ways to choose a winner. If we look closely at
Social choice theory
 Social choice theory A brief introduction Denis Bouyssou CNRS LAMSADE Paris, France Introduction Motivation Aims analyze a number of properties of electoral systems present a few elements of the classical
Social choice theory A brief introduction Denis Bouyssou CNRS LAMSADE Paris, France Introduction Motivation Aims analyze a number of properties of electoral systems present a few elements of the classical
Voting rules: (Dixit and Skeath, ch 14) Recall parkland provision decision:
 rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
rules: (Dixit and Skeath, ch 14) Recall parkland provision decision: Assume - n=10; - total cost of proposed parkland=38; - if provided, each pays equal share = 3.8 - there are two groups of individuals
Introduction to Theory of Voting. Chapter 2 of Computational Social Choice by William Zwicker
 Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Introduction to Theory of Voting Chapter 2 of Computational Social Choice by William Zwicker If we assume Introduction 1. every two voters play equivalent roles in our voting rule 2. every two alternatives
Game Theory. Jiang, Bo ( 江波 )
 Game Theory Jiang, Bo ( 江波 ) Jiang.bo@mail.shufe.edu.cn Mechanism Design in Voting Majority voting Three candidates: x, y, z. Three voters: a, b, c. Voter a: x>y>z; voter b: y>z>x; voter c: z>x>y What
Game Theory Jiang, Bo ( 江波 ) Jiang.bo@mail.shufe.edu.cn Mechanism Design in Voting Majority voting Three candidates: x, y, z. Three voters: a, b, c. Voter a: x>y>z; voter b: y>z>x; voter c: z>x>y What
The Manipulability of Voting Systems. Check off these skills when you feel that you have mastered them.
 Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
Chapter 10 The Manipulability of Voting Systems Chapter Objectives Check off these skills when you feel that you have mastered them. Explain what is meant by voting manipulation. Determine if a voter,
Section Voting Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
Section 15.1 Voting Methods What You Will Learn Plurality Method Borda Count Method Plurality with Elimination Pairwise Comparison Method Tie Breaking 15.1-2 Example 2: Voting for the Honor Society President
SOCIAL CHOICES (Voting Methods) THE PROBLEM. Social Choice and Voting. Terminologies
 SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
SOCIAL CHOICES (Voting Methods) THE PROBLEM In a society, decisions are made by its members in order to come up with a situation that benefits the most. What is the best voting method of arriving at a
Voting System: elections
 Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
Voting System: elections 6 April 25, 2008 Abstract A voting system allows voters to choose between options. And, an election is an important voting system to select a cendidate. In 1951, Arrow s impossibility
Exercises For DATA AND DECISIONS. Part I Voting
 Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
Exercises For DATA AND DECISIONS Part I Voting September 13, 2016 Exercise 1 Suppose that an election has candidates A, B, C, D and E. There are 7 voters, who submit the following ranked ballots: 2 1 1
The Mathematics of Voting. The Mathematics of Voting
 1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
1.3 The Borda Count Method 1 In the Borda Count Method each place on a ballot is assigned points. In an election with N candidates we give 1 point for last place, 2 points for second from last place, and
Chapter 10. The Manipulability of Voting Systems. For All Practical Purposes: Effective Teaching. Chapter Briefing
 Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
Chapter 10 The Manipulability of Voting Systems For All Practical Purposes: Effective Teaching As a teaching assistant, you most likely will administer and proctor many exams. Although it is tempting to
Approval Voting and Scoring Rules with Common Values
 Approval Voting and Scoring Rules with Common Values David S. Ahn University of California, Berkeley Santiago Oliveros University of Essex June 2016 Abstract We compare approval voting with other scoring
Approval Voting and Scoring Rules with Common Values David S. Ahn University of California, Berkeley Santiago Oliveros University of Essex June 2016 Abstract We compare approval voting with other scoring
Algorithms, Games, and Networks February 7, Lecture 8
 Algorithms, Games, and Networks February 7, 2013 Lecturer: Ariel Procaccia Lecture 8 Scribe: Dong Bae Jun 1 Overview In this lecture, we discuss the topic of social choice by exploring voting rules, axioms,
Algorithms, Games, and Networks February 7, 2013 Lecturer: Ariel Procaccia Lecture 8 Scribe: Dong Bae Jun 1 Overview In this lecture, we discuss the topic of social choice by exploring voting rules, axioms,
Strategy and Effectiveness: An Analysis of Preferential Ballot Voting Methods
 Strategy and Effectiveness: An Analysis of Preferential Ballot Voting Methods Maksim Albert Tabachnik Advisor: Dr. Hubert Bray April 25, 2011 Submitted for Graduation with Distinction: Duke University
Strategy and Effectiveness: An Analysis of Preferential Ballot Voting Methods Maksim Albert Tabachnik Advisor: Dr. Hubert Bray April 25, 2011 Submitted for Graduation with Distinction: Duke University
Rationality of Voting and Voting Systems: Lecture II
 Rationality of Voting and Voting Systems: Lecture II Rationality of Voting Systems Hannu Nurmi Department of Political Science University of Turku Three Lectures at National Research University Higher
Rationality of Voting and Voting Systems: Lecture II Rationality of Voting Systems Hannu Nurmi Department of Political Science University of Turku Three Lectures at National Research University Higher
Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate.
 Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
Math 13 HW 5 Chapter 9 Write all responses on separate paper. Use complete sentences, charts and diagrams, as appropriate. 1. Explain why majority rule is not a good way to choose between four alternatives.
Many Social Choice Rules
 Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
Many Social Choice Rules 1 Introduction So far, I have mentioned several of the most commonly used social choice rules : pairwise majority rule, plurality, plurality with a single run off, the Borda count.
Voting Methods for Municipal Elections: Propaganda, Field Experiments and what USA voters want from an Election Algorithm
 Voting Methods for Municipal Elections: Propaganda, Field Experiments and what USA voters want from an Election Algorithm Kathryn Lenz, Mathematics and Statistics Department, University of Minnesota Duluth
Voting Methods for Municipal Elections: Propaganda, Field Experiments and what USA voters want from an Election Algorithm Kathryn Lenz, Mathematics and Statistics Department, University of Minnesota Duluth
History of Social Choice and Welfare Economics
 What is Social Choice Theory? History of Social Choice and Welfare Economics SCT concerned with evaluation of alternative methods of collective decision making and logical foundations of welfare economics
What is Social Choice Theory? History of Social Choice and Welfare Economics SCT concerned with evaluation of alternative methods of collective decision making and logical foundations of welfare economics
Electing the President. Chapter 12 Mathematical Modeling
 Electing the President Chapter 12 Mathematical Modeling Phases of the Election 1. State Primaries seeking nomination how to position the candidate to gather momentum in a set of contests 2. Conventions
Electing the President Chapter 12 Mathematical Modeling Phases of the Election 1. State Primaries seeking nomination how to position the candidate to gather momentum in a set of contests 2. Conventions
Intro to Contemporary Math
 Intro to Contemporary Math Independence of Irrelevant Alternatives Criteria Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Independence of Irrelevant Alternatives Criteria
Intro to Contemporary Math Independence of Irrelevant Alternatives Criteria Nicholas Nguyen nicholas.nguyen@uky.edu Department of Mathematics UK Agenda Independence of Irrelevant Alternatives Criteria
Election Theory. How voters and parties behave strategically in democratic systems. Mark Crowley
 How voters and parties behave strategically in democratic systems Department of Computer Science University of British Columbia January 30, 2006 Sources Voting Theory Jeff Gill and Jason Gainous. "Why
How voters and parties behave strategically in democratic systems Department of Computer Science University of British Columbia January 30, 2006 Sources Voting Theory Jeff Gill and Jason Gainous. "Why
The Borda Majority Count
 The Borda Majority Count Manzoor Ahmad Zahid Harrie de Swart Department of Philosophy, Tilburg University Box 90153, 5000 LE Tilburg, The Netherlands; Email: {M.A.Zahid, H.C.M.deSwart}@uvt.nl Abstract
The Borda Majority Count Manzoor Ahmad Zahid Harrie de Swart Department of Philosophy, Tilburg University Box 90153, 5000 LE Tilburg, The Netherlands; Email: {M.A.Zahid, H.C.M.deSwart}@uvt.nl Abstract
A Characterization of the Maximin Rule in the Context of Voting
 of the Maximin Rule 1 de 33 of the Maximin Rule in the Context of Voting Ronan Congar & Vincent Merlin CARE, Université de Rouen & CREM, CNRS and Université de Caen New Approaches to Voting and Social
of the Maximin Rule 1 de 33 of the Maximin Rule in the Context of Voting Ronan Congar & Vincent Merlin CARE, Université de Rouen & CREM, CNRS and Université de Caen New Approaches to Voting and Social
Math for Liberal Arts MAT 110: Chapter 12 Notes
 Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
Math for Liberal Arts MAT 110: Chapter 12 Notes Voting Methods David J. Gisch Voting: Does the Majority Always Rule? Choosing a Winner In elections with more then 2 candidates, there are several acceptable
The Problem with Majority Rule. Shepsle and Bonchek Chapter 4
 The Problem with Majority Rule Shepsle and Bonchek Chapter 4 Majority Rule is problematic 1. Who s the majority? 2. Sometimes there is no decisive winner Condorcet s paradox: A group composed of individuals
The Problem with Majority Rule Shepsle and Bonchek Chapter 4 Majority Rule is problematic 1. Who s the majority? 2. Sometimes there is no decisive winner Condorcet s paradox: A group composed of individuals
The Math of Rational Choice - Math 100 Spring 2015
 The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
The Math of Rational Choice - Math 100 Spring 2015 Mathematics can be used to understand many aspects of decision-making in everyday life, such as: 1. Voting (a) Choosing a restaurant (b) Electing a leader
Constructing voting paradoxes with logic and symmetry Teacher s Notes
 Constructing voting paradoxes with logic and symmetry Teacher s Notes Elena Galaktionova elena@problemtrove.org Mobile Math Circle This is a loose transcript of the Math Circle, with occasional notes on
Constructing voting paradoxes with logic and symmetry Teacher s Notes Elena Galaktionova elena@problemtrove.org Mobile Math Circle This is a loose transcript of the Math Circle, with occasional notes on
Voting and Electoral Competition
 Voting and Electoral Competition Prof. Panu Poutvaara University of Munich and Ifo Institute On the organization of the course Lectures, exam at the end Articles to read. In more technical articles, it
Voting and Electoral Competition Prof. Panu Poutvaara University of Munich and Ifo Institute On the organization of the course Lectures, exam at the end Articles to read. In more technical articles, it
