Chapter 8: Recursion
|
|
|
- Kimberly Fitzgerald
- 6 years ago
- Views:
Transcription
1 Chapter 8: Recursion Presentation slides for Java Software Solutions for AP* Computer Science 3rd Edition by John Lewis, William Loftus, and Cara Cocking Java Software Solutions is published by Addison-Wesley Presentation slides are copyright 2006 by John Lewis, William Loftus, and Cara Cocking. All rights reserved. Instructors using the textbook may use and modify these slides for pedagogical purposes. *AP is a registered trademark of The College Entrance Examination Board which was not involved in the production of, and does not endorse, this product.
2 Recursion Ø Recursion is a fundamental programming technique that can provide elegant solutions certain kinds of problems Ø Chapter 8 focuses on: thinking in a recursive manner programming in a recursive manner the correct use of recursion examples using recursion recursion in sorting recursion in graphics 2
3 Recursive Thinking Ø Recursion is a programming technique in which a method can call itself to solve a problem Ø A recursive definition is one which uses the word or concept being defined in the definition itself; when defining an English word, a recursive definition usually is not helpful Ø But in other situations, a recursive definition can be an appropriate way to express a concept Ø Before applying recursion to programming, it is best to practice thinking recursively 3
4 Recursive Definitions Ø Consider the following list of numbers: 24, 88, 40, 37 Ø A list can be defined recursively A LIST is a: number or a: number comma LIST Ø That is, a LIST is defined to be a single number, or a number followed by a comma followed by a LIST Ø The concept of a LIST is used to define itself 4
5 Recursive Definitions Ø The recursive part of the LIST definition is used several times, ultimately terminating with the nonrecursive part: number comma LIST 24, 88, 40, 37 number comma LIST 88, 40, 37 number comma LIST 40, 37 number 37 5
6 Infinite Recursion Ø All recursive definitions must have a non-recursive part Ø If they don't, there is no way to terminate the recursive path Ø A definition without a non-recursive part causes infinite recursion Ø This problem is similar to an infinite loop with the definition itself causing the infinite loop Ø The non-recursive part often is called the base case 6
7 Recursive Definitions Ø Mathematical formulas often are expressed recursively Ø N!, for any positive integer N, is defined to be the product of all integers between 1 and N inclusive Ø This definition can be expressed recursively as: 1! = 1 N! = N * (N-1)! Ø The concept of the factorial is defined in terms of another factorial until the base case of 1! is reached 7
8 Recursive Definitions 5! 5 * 4! * 3! 6 3 * 2! 2 * 1! 2 1 8
9 Recursive Programming Ø A method in Java can invoke itself; if set up that way, it is called a recursive method Ø The code of a recursive method must be structured to handle both the base case and the recursive case Ø Each call to the method sets up a new execution environment, with new parameters and new local variables Ø As always, when the method execution completes, control returns to the method that invoked it (which may be an earlier invocation of itself) 9
10 Recursive Programming Ø Consider the problem of computing the sum of all the numbers between 1 and any positive integer N, inclusive Ø This problem can be expressed recursively as: N i = 1 N-1 = N + = N + (N-1) + i = 1 N-2 i = 1 = etc. 10
11 Recursive Programming public int sum (int num) { } int result; if (num == 1) else result = 1; result = num + sum (num - 1); return result; 11
12 Recursive Programming main result = 6 sum(3) sum result = 3 sum(2) sum result = 1 sum(1) sum 12
13 Recursion vs. Iteration Ø Just because we can use recursion to solve a problem, doesn't mean we should Ø For instance, we usually would not use recursion to solve the sum of 1 to N problem, because the iterative version is easier to understand; in fact, there is a formula which is superior to both recursion and iteration! Ø You must be able to determine when recursion is the correct technique to use 13
14 Recursion vs. Iteration Ø Every recursive solution has a corresponding iterative solution Ø For example, the sum (or the product) of the numbers between 1 and any positive integer N can be calculated with a for loop Ø Recursion has the overhead of multiple method invocations Ø Nevertheless, recursive solutions often are more simple and elegant than iterative solutions 14
15 Indirect Recursion Ø A method invoking itself is considered to be direct recursion Ø A method could invoke another method, which invokes another, etc., until eventually the original method is invoked again Ø For example, method m1 could invoke m2, which invokes m3, which in turn invokes m1 again until a base case is reached Ø This is called indirect recursion, and requires all the same care as direct recursion Ø It is often more difficult to trace and debug 15
16 Indirect Recursion m1 m2 m3 m1 m2 m3 m1 m2 m3 16
17 Maze Traversal Ø We can use recursion to find a path through a maze; a path can be found from any location if a path can be found from any of the location s neighboring locations Ø At each location we encounter, we mark the location as visited and we attempt to find a path from that location s unvisited neighbors Ø Recursion keeps track of the path through the maze Ø The base cases are an prohibited move or arrival at the final destination 17
18 Maze Traversal Ø See MazeSearch.java (page 473) Ø See Maze.java (page 474) 18
19 Towers of Hanoi Ø The Towers of Hanoi is a puzzle made up of three vertical pegs and several disks that slide on the pegs Ø The disks are of varying size, initially placed on one peg with the largest disk on the bottom with increasingly smaller disks on top Ø The goal is to move all of the disks from one peg to another according to the following rules: We can move only one disk at a time We cannot place a larger disk on top of a smaller disk All disks must be on some peg except for the disk in transit between pegs 19
20 Towers of Hanoi Ø A solution to the three-disk Towers of Hanoi puzzle Ø See Figures 8.5 and
21 Towers of Hanoi Ø To move a stack of N disks from the original peg to the destination peg move the topmost N - 1 disks from the original peg to the extra peg move the largest disk from the original peg to the destination peg move the N-1 disks from the extra peg to the destination peg The base case occurs when a stack consists of only one disk Ø This recursive solution is simple and elegant even though the number of move increases exponentially as the number of disks increases Ø The iterative solution to the Towers of Hanoi is much more complex 21
22 Towers of Hanoi Ø See SolveTowers.java (page 479) Ø See TowersOfHanoi.java (page 480) 22
23 Recursion in Sorting Ø Some sorting algorithms can be implemented recursively Ø We will examine two: Merge sort Quick sort 23
24 Merge Sort Ø Merge sort divides a list in half, recursively sorts each half, and then combines the two lists Ø At the deepest level of recursion, one-element lists are reached Ø A one-element list is already sorted Ø The work of the sort comes in when the sorted sublists are merge together Ø Merge sort has efficiency O(n log n) Ø See RecursiveSorts.java (page 483) 24
25 Quick Sort Ø Quick sort partitions a list into two sublists and recursively sorts each sublist Ø Partitioning is done by selecting a pivot value Ø Every element less than the pivot is moved to the left of it Ø Every element greater than the pivot is moved to the right of it Ø The work of the sort is in the partitioning Ø Quick sort has efficiency O(n log n) Ø See RecursiveSorts.java (page 483) 25
26 Recursion in Graphics Ø Consider the task of repeatedly displaying a set of tiled images in a mosaic in which one of the tiles contains a copy of the entire collage Ø The base case is reached when the area for the remaining tile shrinks to a certain size Ø See TiledPictures.java (page 490) 26
27 Fractals Ø A fractal is a geometric shape than can consist of the same pattern repeated in different scales and orientations Ø The Koch Snowflake is a particular fractal that begins with an equilateral triangle Ø To get a higher order of the fractal, the middle of each edge is replaced with two angled line segments 27
28 Fractals Ø See Figure 8.9 Ø See KochSnowflake.java (page 493) Ø See KochPanel.java (page 496) 28
29 Summary Ø Chapter 8 has focused on: thinking in a recursive manner programming in a recursive manner the correct use of recursion examples using recursion recursion in sorting recursion in graphics 29
Comparison Sorts. EECS 2011 Prof. J. Elder - 1 -
 Comparison Sorts - 1 - Sorting Ø We have seen the advantage of sorted data representations for a number of applications q Sparse vectors q Maps q Dictionaries Ø Here we consider the problem of how to efficiently
Comparison Sorts - 1 - Sorting Ø We have seen the advantage of sorted data representations for a number of applications q Sparse vectors q Maps q Dictionaries Ø Here we consider the problem of how to efficiently
Priority Queues & Heaps
 Priority Queues & Heaps Chapter 8-1 - The Java Collections Framework (Ordered Data Types) Interface Abstract Class Class Iterable Collection Queue Abstract Collection List Abstract Queue Abstract List
Priority Queues & Heaps Chapter 8-1 - The Java Collections Framework (Ordered Data Types) Interface Abstract Class Class Iterable Collection Queue Abstract Collection List Abstract Queue Abstract List
Priority Queues & Heaps
 Priority Queues & Heaps - 1 - Outline Ø The Priority Queue class of the Java Collections Framework Ø Total orderings, the Comparable Interface and the Comparator Class Ø Heaps Ø Adaptable Priority Queues
Priority Queues & Heaps - 1 - Outline Ø The Priority Queue class of the Java Collections Framework Ø Total orderings, the Comparable Interface and the Comparator Class Ø Heaps Ø Adaptable Priority Queues
Priority Queues & Heaps
 Priority Queues & Heaps - 1 - Outline Ø The Priority Queue ADT Ø Total orderings, the Comparable Interface and the Comparator Class Ø Heaps Ø Adaptable Priority Queues - 2 - Outcomes Ø By understanding
Priority Queues & Heaps - 1 - Outline Ø The Priority Queue ADT Ø Total orderings, the Comparable Interface and the Comparator Class Ø Heaps Ø Adaptable Priority Queues - 2 - Outcomes Ø By understanding
Hoboken Public Schools. Algebra II Honors Curriculum
 Hoboken Public Schools Algebra II Honors Curriculum Algebra Two Honors HOBOKEN PUBLIC SCHOOLS Course Description Algebra II Honors continues to build students understanding of the concepts that provide
Hoboken Public Schools Algebra II Honors Curriculum Algebra Two Honors HOBOKEN PUBLIC SCHOOLS Course Description Algebra II Honors continues to build students understanding of the concepts that provide
Midterm Review. EECS 2011 Prof. J. Elder - 1 -
 Midterm Review - 1 - Topics on the Midterm Ø Data Structures & Object-Oriented Design Ø Run-Time Analysis Ø Linear Data Structures Ø The Java Collections Framework Ø Recursion Ø Trees Ø Priority Queues
Midterm Review - 1 - Topics on the Midterm Ø Data Structures & Object-Oriented Design Ø Run-Time Analysis Ø Linear Data Structures Ø The Java Collections Framework Ø Recursion Ø Trees Ø Priority Queues
Tie Breaking in STV. 1 Introduction. 3 The special case of ties with the Meek algorithm. 2 Ties in practice
 Tie Breaking in STV 1 Introduction B. A. Wichmann Brian.Wichmann@bcs.org.uk Given any specific counting rule, it is necessary to introduce some words to cover the situation in which a tie occurs. However,
Tie Breaking in STV 1 Introduction B. A. Wichmann Brian.Wichmann@bcs.org.uk Given any specific counting rule, it is necessary to introduce some words to cover the situation in which a tie occurs. However,
Hoboken Public Schools. AP Calculus Curriculum
 Hoboken Public Schools AP Calculus Curriculum AP Calculus HOBOKEN PUBLIC SCHOOLS Course Description An Advanced Placement (AP) course in calculus consists of a full high school academic year of work that
Hoboken Public Schools AP Calculus Curriculum AP Calculus HOBOKEN PUBLIC SCHOOLS Course Description An Advanced Placement (AP) course in calculus consists of a full high school academic year of work that
Search Trees. Chapter 10. CSE 2011 Prof. J. Elder Last Updated: :51 PM
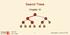 Search Trees Chapter 1 < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Binary Search Trees Ø A binary search tree is a binary tree storing key-value entries at its internal
Search Trees Chapter 1 < 6 2 > 1 4 = 8 9-1 - Outline Ø Binary Search Trees Ø AVL Trees Ø Splay Trees - 2 - Binary Search Trees Ø A binary search tree is a binary tree storing key-value entries at its internal
ECE250: Algorithms and Data Structures Trees
 ECE250: Algorithms and Data Structures Trees Ladan Tahvildari, PEng, SMIEEE Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University of Waterloo Materials from
ECE250: Algorithms and Data Structures Trees Ladan Tahvildari, PEng, SMIEEE Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University of Waterloo Materials from
Text UI. Data Store Ø Example of a backend to a real Could add a different user interface. Good judgment comes from experience
 Reviewing Lab 10 Text UI Created two classes Ø Used one class within another class Ø Tested them Graphical UI Backend Data Store Ø Example of a backend to a real applica@on Could add a different user interface
Reviewing Lab 10 Text UI Created two classes Ø Used one class within another class Ø Tested them Graphical UI Backend Data Store Ø Example of a backend to a real applica@on Could add a different user interface
Plan For the Week. Solve problems by programming in Python. Compsci 101 Way-of-life. Vocabulary and Concepts
 Plan For the Week Solve problems by programming in Python Ø Like to do "real-world" problems, but we're very new to the language Ø Learn the syntax and semantics of simple Python programs Compsci 101 Way-of-life
Plan For the Week Solve problems by programming in Python Ø Like to do "real-world" problems, but we're very new to the language Ø Learn the syntax and semantics of simple Python programs Compsci 101 Way-of-life
STUDY GUIDE FOR TEST 2
 STUDY GUIDE FOR TEST 2 MATH 303. SPRING 2006. INSTRUCTOR: PROFESSOR AITKEN The test will cover Chapters 4, 5, and 6. Chapter 4: The Mathematics of Voting Sample Exercises: 1, 3, 5, 7, 8, 10, 14, 15, 17,
STUDY GUIDE FOR TEST 2 MATH 303. SPRING 2006. INSTRUCTOR: PROFESSOR AITKEN The test will cover Chapters 4, 5, and 6. Chapter 4: The Mathematics of Voting Sample Exercises: 1, 3, 5, 7, 8, 10, 14, 15, 17,
Midterm Review. EECS 2011 Prof. J. Elder - 1 -
 Midterm Review - 1 - Topics on the Midterm Ø Data Structures & Object-Oriented Design Ø Run-Time Analysis Ø Linear Data Structures Ø The Java Collections Framework Ø Recursion Ø Trees Ø Priority Queues
Midterm Review - 1 - Topics on the Midterm Ø Data Structures & Object-Oriented Design Ø Run-Time Analysis Ø Linear Data Structures Ø The Java Collections Framework Ø Recursion Ø Trees Ø Priority Queues
Essential Questions Content Skills Assessments Standards/PIs. Identify prime and composite numbers, GCF, and prime factorization.
 Map: MVMS Math 7 Type: Consensus Grade Level: 7 School Year: 2007-2008 Author: Paula Barnes District/Building: Minisink Valley CSD/Middle School Created: 10/19/2007 Last Updated: 11/06/2007 How does the
Map: MVMS Math 7 Type: Consensus Grade Level: 7 School Year: 2007-2008 Author: Paula Barnes District/Building: Minisink Valley CSD/Middle School Created: 10/19/2007 Last Updated: 11/06/2007 How does the
Estimating the Margin of Victory for Instant-Runoff Voting
 Estimating the Margin of Victory for Instant-Runoff Voting David Cary Abstract A general definition is proposed for the margin of victory of an election contest. That definition is applied to Instant Runoff
Estimating the Margin of Victory for Instant-Runoff Voting David Cary Abstract A general definition is proposed for the margin of victory of an election contest. That definition is applied to Instant Runoff
IDENTIFYING FAULT-PRONE MODULES IN SOFTWARE FOR DIAGNOSIS AND TREATMENT USING EEPORTERS CLASSIFICATION TREE
 IDENTIFYING FAULT-PRONE MODULES IN SOFTWARE FOR DIAGNOSIS AND TREATMENT USING EEPORTERS CLASSIFICATION TREE Bassey. A. Ekanem 1, Nseabasi Essien 2 1 Department of Computer Science, Delta State Polytechnic,
IDENTIFYING FAULT-PRONE MODULES IN SOFTWARE FOR DIAGNOSIS AND TREATMENT USING EEPORTERS CLASSIFICATION TREE Bassey. A. Ekanem 1, Nseabasi Essien 2 1 Department of Computer Science, Delta State Polytechnic,
Andreas Fring. Basic Operations
 Basic Operations Creating a workbook: The first action should always be to give your workbook a name and save it on your computer. Go for this to the menu bar and select by left mouse click (LC): Ø File
Basic Operations Creating a workbook: The first action should always be to give your workbook a name and save it on your computer. Go for this to the menu bar and select by left mouse click (LC): Ø File
Title: Local Search Required reading: AIMA, Chapter 4 LWH: Chapters 6, 10, 13 and 14.
 B.Y. Choueiry 1 Instructor s notes #8 Title: Local Search Required reading: AIMA, Chapter 4 LWH: Chapters 6, 10, 13 and 14. Introduction to Artificial Intelligence CSCE 476-876, Fall 2017 URL: www.cse.unl.edu/
B.Y. Choueiry 1 Instructor s notes #8 Title: Local Search Required reading: AIMA, Chapter 4 LWH: Chapters 6, 10, 13 and 14. Introduction to Artificial Intelligence CSCE 476-876, Fall 2017 URL: www.cse.unl.edu/
Fall 2016 COP 3223H Program #5: Election Season Nears an End Due date: Please consult WebCourses for your section
 Fall 2016 COP 3223H Program #5: Election Season Nears an End Due date: Please consult WebCourses for your section Objective(s) 1. To learn how to use 1D arrays to solve a problem in C. Problem A: Expected
Fall 2016 COP 3223H Program #5: Election Season Nears an End Due date: Please consult WebCourses for your section Objective(s) 1. To learn how to use 1D arrays to solve a problem in C. Problem A: Expected
Hoboken Public Schools. College Algebra Curriculum
 Hoboken Public Schools College Algebra Curriculum College Algebra HOBOKEN PUBLIC SCHOOLS Course Description College Algebra reflects the New Jersey learning standards at the high school level and is designed
Hoboken Public Schools College Algebra Curriculum College Algebra HOBOKEN PUBLIC SCHOOLS Course Description College Algebra reflects the New Jersey learning standards at the high school level and is designed
Hoboken Public Schools. Project Lead The Way Curriculum Grade 8
 Hoboken Public Schools Project Lead The Way Curriculum Grade 8 Project Lead The Way HOBOKEN PUBLIC SCHOOLS Course Description PLTW Gateway s 9 units empower students to lead their own discovery. The hands-on
Hoboken Public Schools Project Lead The Way Curriculum Grade 8 Project Lead The Way HOBOKEN PUBLIC SCHOOLS Course Description PLTW Gateway s 9 units empower students to lead their own discovery. The hands-on
Chapter 11. Weighted Voting Systems. For All Practical Purposes: Effective Teaching
 Chapter Weighted Voting Systems For All Practical Purposes: Effective Teaching In observing other faculty or TA s, if you discover a teaching technique that you feel was particularly effective, don t hesitate
Chapter Weighted Voting Systems For All Practical Purposes: Effective Teaching In observing other faculty or TA s, if you discover a teaching technique that you feel was particularly effective, don t hesitate
Hoboken Public Schools. Geometry Curriculum
 Hoboken Public Schools Geometry Curriculum Geometry HOBOKEN PUBLIC SCHOOLS Course Description The Geometry courses present the core content necessary to promote geometric proficiency and prepare students
Hoboken Public Schools Geometry Curriculum Geometry HOBOKEN PUBLIC SCHOOLS Course Description The Geometry courses present the core content necessary to promote geometric proficiency and prepare students
Maps and Hash Tables. EECS 2011 Prof. J. Elder - 1 -
 Maps and Hash Tables - 1 - Outline Ø Maps Ø Hashing Ø Multimaps Ø Ordered Maps - 2 - Learning Outcomes Ø By understanding this lecture, you should be able to: Ø Outline the ADT for a map and a multimap
Maps and Hash Tables - 1 - Outline Ø Maps Ø Hashing Ø Multimaps Ø Ordered Maps - 2 - Learning Outcomes Ø By understanding this lecture, you should be able to: Ø Outline the ADT for a map and a multimap
CS 5523: Operating Systems
 Lecture1: OS Overview CS 5523: Operating Systems Instructor: Dr Tongping Liu Midterm Exam: Oct 2, 2017, Monday 7:20pm 8:45pm Operating System: what is it?! Evolution of Computer Systems and OS Concepts
Lecture1: OS Overview CS 5523: Operating Systems Instructor: Dr Tongping Liu Midterm Exam: Oct 2, 2017, Monday 7:20pm 8:45pm Operating System: what is it?! Evolution of Computer Systems and OS Concepts
File Systems: Fundamentals
 File Systems: Fundamentals 1 Files What is a file? Ø A named collection of related information recorded on secondary storage (e.g., disks) File attributes Ø Name, type, location, size, protection, creator,
File Systems: Fundamentals 1 Files What is a file? Ø A named collection of related information recorded on secondary storage (e.g., disks) File attributes Ø Name, type, location, size, protection, creator,
Uninformed search. Lirong Xia
 Uninformed search Lirong Xia Spring, 2017 Today s schedule ØRational agents ØSearch problems State space graph: modeling the problem Search trees: scratch paper for solution ØUninformed search Depth first
Uninformed search Lirong Xia Spring, 2017 Today s schedule ØRational agents ØSearch problems State space graph: modeling the problem Search trees: scratch paper for solution ØUninformed search Depth first
Apple s Audio Units Logo License Agreement for Hosting Applications
 Apple s Audio Units Logo License Agreement for Hosting Applications This Audio Units Logo License Agreement ( Agreement ) is entered into by and between Apple Computer, Inc. at 1 Infinite Loop, Cupertino,
Apple s Audio Units Logo License Agreement for Hosting Applications This Audio Units Logo License Agreement ( Agreement ) is entered into by and between Apple Computer, Inc. at 1 Infinite Loop, Cupertino,
Do two parties represent the US? Clustering analysis of US public ideology survey
 Do two parties represent the US? Clustering analysis of US public ideology survey Louisa Lee 1 and Siyu Zhang 2, 3 Advised by: Vicky Chuqiao Yang 1 1 Department of Engineering Sciences and Applied Mathematics,
Do two parties represent the US? Clustering analysis of US public ideology survey Louisa Lee 1 and Siyu Zhang 2, 3 Advised by: Vicky Chuqiao Yang 1 1 Department of Engineering Sciences and Applied Mathematics,
Hoboken Public Schools. AP Statistics Curriculum
 Hoboken Public Schools AP Statistics Curriculum AP Statistics HOBOKEN PUBLIC SCHOOLS Course Description AP Statistics is the high school equivalent of a one semester, introductory college statistics course.
Hoboken Public Schools AP Statistics Curriculum AP Statistics HOBOKEN PUBLIC SCHOOLS Course Description AP Statistics is the high school equivalent of a one semester, introductory college statistics course.
The Effectiveness of Receipt-Based Attacks on ThreeBallot
 The Effectiveness of Receipt-Based Attacks on ThreeBallot Kevin Henry, Douglas R. Stinson, Jiayuan Sui David R. Cheriton School of Computer Science University of Waterloo Waterloo, N, N2L 3G1, Canada {k2henry,
The Effectiveness of Receipt-Based Attacks on ThreeBallot Kevin Henry, Douglas R. Stinson, Jiayuan Sui David R. Cheriton School of Computer Science University of Waterloo Waterloo, N, N2L 3G1, Canada {k2henry,
Overview. Ø Neural Networks are considered black-box models Ø They are complex and do not provide much insight into variable relationships
 Neural Networks Overview Ø s are considered black-box models Ø They are complex and do not provide much insight into variable relationships Ø They have the potential to model very complicated patterns
Neural Networks Overview Ø s are considered black-box models Ø They are complex and do not provide much insight into variable relationships Ø They have the potential to model very complicated patterns
Section Apportionment Methods. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 15.3 Apportionment Methods What You Will Learn Standard Divisor Standard Quota Lower Quota Upper Quota Hamilton s Method The Quota Rule Jefferson s Method Webster s Method Adam s Method 15.3-2
Section 15.3 Apportionment Methods What You Will Learn Standard Divisor Standard Quota Lower Quota Upper Quota Hamilton s Method The Quota Rule Jefferson s Method Webster s Method Adam s Method 15.3-2
Cluster Analysis. (see also: Segmentation)
 Cluster Analysis (see also: Segmentation) Cluster Analysis Ø Unsupervised: no target variable for training Ø Partition the data into groups (clusters) so that: Ø Observations within a cluster are similar
Cluster Analysis (see also: Segmentation) Cluster Analysis Ø Unsupervised: no target variable for training Ø Partition the data into groups (clusters) so that: Ø Observations within a cluster are similar
Maps, Hash Tables and Dictionaries
 Maps, Hash Tables and Dictionaries Chapter 9-1 - Outline Ø Maps Ø Hashing Ø Dictionaries Ø Ordered Maps & Dictionaries - 2 - Outline Ø Maps Ø Hashing Ø Dictionaries Ø Ordered Maps & Dictionaries - 3 -
Maps, Hash Tables and Dictionaries Chapter 9-1 - Outline Ø Maps Ø Hashing Ø Dictionaries Ø Ordered Maps & Dictionaries - 2 - Outline Ø Maps Ø Hashing Ø Dictionaries Ø Ordered Maps & Dictionaries - 3 -
Subreddit Recommendations within Reddit Communities
 Subreddit Recommendations within Reddit Communities Vishnu Sundaresan, Irving Hsu, Daryl Chang Stanford University, Department of Computer Science ABSTRACT: We describe the creation of a recommendation
Subreddit Recommendations within Reddit Communities Vishnu Sundaresan, Irving Hsu, Daryl Chang Stanford University, Department of Computer Science ABSTRACT: We describe the creation of a recommendation
NEW YORK CITY COLLEGE OF TECHNOLOGY The City University of New York
 NEW YORK CITY COLLEGE OF TECHNOLOGY The City University of New York DEPARTMENT: Mathematics COURSE: MAT 2440/ MA 440 TITLE: DESCRIPTION: TEXTS: Discrete Structures and Algorithms I This course introduces
NEW YORK CITY COLLEGE OF TECHNOLOGY The City University of New York DEPARTMENT: Mathematics COURSE: MAT 2440/ MA 440 TITLE: DESCRIPTION: TEXTS: Discrete Structures and Algorithms I This course introduces
Hoboken Public Schools. PLTW Introduction to Computer Science Curriculum
 Hoboken Public Schools PLTW Introduction to Computer Science Curriculum Introduction to Computer Science Curriculum HOBOKEN PUBLIC SCHOOLS Course Description Introduction to Computer Science Design (ICS)
Hoboken Public Schools PLTW Introduction to Computer Science Curriculum Introduction to Computer Science Curriculum HOBOKEN PUBLIC SCHOOLS Course Description Introduction to Computer Science Design (ICS)
Chapter 1: Number Concepts
 Office of Curriculum and Instruction Content Area: MATHEMATICS Domains: Grade Level: 2 Pacing: 10 Days Chapter 1: Number Concepts Numbers and Operations in Base Ten Operations and Algebraic Thinking New
Office of Curriculum and Instruction Content Area: MATHEMATICS Domains: Grade Level: 2 Pacing: 10 Days Chapter 1: Number Concepts Numbers and Operations in Base Ten Operations and Algebraic Thinking New
Deadlock. deadlock analysis - primitive processes, parallel composition, avoidance
 Deadlock CDS News: Brainy IBM Chip Packs One Million Neuron Punch Overview: ideas, 4 four necessary and sufficient conditions deadlock analysis - primitive processes, parallel composition, avoidance the
Deadlock CDS News: Brainy IBM Chip Packs One Million Neuron Punch Overview: ideas, 4 four necessary and sufficient conditions deadlock analysis - primitive processes, parallel composition, avoidance the
Proving correctness of Stable Matching algorithm Analyzing algorithms Asymptotic running times
 Objectives Proving correctness of Stable Matching algorithm Analyzing algorithms Asymptotic running times Wiki notes: Read after class; I am giving loose guidelines the point is to review and synthesize
Objectives Proving correctness of Stable Matching algorithm Analyzing algorithms Asymptotic running times Wiki notes: Read after class; I am giving loose guidelines the point is to review and synthesize
30 Transformational Design with Essential Aspect Decomposition: Model-Driven Architecture (MDA)
 Fakultät Informatik, Institut für Software- und Multimediatechnik, Lehrstuhl für Softwaretechnologie 30 Transformational Design with Essential Aspect Decomposition: Model-Driven Architecture () Prof. Dr.
Fakultät Informatik, Institut für Software- und Multimediatechnik, Lehrstuhl für Softwaretechnologie 30 Transformational Design with Essential Aspect Decomposition: Model-Driven Architecture () Prof. Dr.
Aspect Decomposition: Model-Driven Architecture (MDA) 30 Transformational Design with Essential. References. Ø Optional: Ø Obligatory:
 Fakultät Informatik, Institut für Software- und Multimediatechnik, Lehrstuhl für Softwaretechnologie 30 Transformational Design with Essential Aspect Decomposition: Model-Driven Architecture () Prof. Dr.
Fakultät Informatik, Institut für Software- und Multimediatechnik, Lehrstuhl für Softwaretechnologie 30 Transformational Design with Essential Aspect Decomposition: Model-Driven Architecture () Prof. Dr.
Optimization Strategies
 Global Memory Access Pattern and Control Flow Objectives Ø Ø Global Memory Access Pattern (Coalescing) Ø Control Flow (Divergent branch) Copyright 2013 by Yong Cao, Referencing UIUC ECE498AL Course Notes
Global Memory Access Pattern and Control Flow Objectives Ø Ø Global Memory Access Pattern (Coalescing) Ø Control Flow (Divergent branch) Copyright 2013 by Yong Cao, Referencing UIUC ECE498AL Course Notes
Political Districting for Elections to the German Bundestag: An Optimization-Based Multi-Stage Heuristic Respecting Administrative Boundaries
 Political Districting for Elections to the German Bundestag: An Optimization-Based Multi-Stage Heuristic Respecting Administrative Boundaries Sebastian Goderbauer 1 Electoral Districts in Elections to
Political Districting for Elections to the German Bundestag: An Optimization-Based Multi-Stage Heuristic Respecting Administrative Boundaries Sebastian Goderbauer 1 Electoral Districts in Elections to
Creating and Managing Clauses. Selectica, Inc. Selectica Contract Performance Management System
 Selectica, Inc. Selectica Contract Performance Management System Copyright 2006 Selectica, Inc. Copyright 2007 Selectica, Inc. 1740 Technology Drive, Suite 450 San Jose, CA 95110 http://www.selectica.com
Selectica, Inc. Selectica Contract Performance Management System Copyright 2006 Selectica, Inc. Copyright 2007 Selectica, Inc. 1740 Technology Drive, Suite 450 San Jose, CA 95110 http://www.selectica.com
One View Watchlists Implementation Guide Release 9.2
 [1]JD Edwards EnterpriseOne Applications One View Watchlists Implementation Guide Release 9.2 E63996-03 April 2017 Describes One View Watchlists and discusses how to add and modify One View Watchlists.
[1]JD Edwards EnterpriseOne Applications One View Watchlists Implementation Guide Release 9.2 E63996-03 April 2017 Describes One View Watchlists and discusses how to add and modify One View Watchlists.
Year 1 Mental mathematics and fluency in rapid recall of number facts are one of the main aims of the new Mathematics Curriculum.
 Year 1 by the end of Year 1. Ø Recite numbers to 100 forwards and backwards from any number Ø Read and write numbers to 100 in numerals Ø Read and write numbers to 20 in words Ø Order numbers to 100 Ø
Year 1 by the end of Year 1. Ø Recite numbers to 100 forwards and backwards from any number Ø Read and write numbers to 100 in numerals Ø Read and write numbers to 20 in words Ø Order numbers to 100 Ø
Mixed-Strategies for Linear Tabling in Prolog
 Mixed-Strategies for Linear Tabling in Prolog CRACS & INESC-Porto LA Faculty of Sciences, University of Porto, Portugal miguel-areias@dcc.fc.up.pt ricroc@dcc.fc.up.pt INForum-CoRTA 2010, Braga, Portugal,
Mixed-Strategies for Linear Tabling in Prolog CRACS & INESC-Porto LA Faculty of Sciences, University of Porto, Portugal miguel-areias@dcc.fc.up.pt ricroc@dcc.fc.up.pt INForum-CoRTA 2010, Braga, Portugal,
TAFTW (Take Aways for the Week) APT Quiz and Markov Overview. Comparing objects and tradeoffs. From Comparable to TreeMap/Sort
 TAFTW (Take Aways for the Week) Graded work this week: Ø APT Quiz, details and overview Ø Markov assignment, details and overview Concepts: Empirical and Analytical Analysis Ø Algorithms and Data Structures
TAFTW (Take Aways for the Week) Graded work this week: Ø APT Quiz, details and overview Ø Markov assignment, details and overview Concepts: Empirical and Analytical Analysis Ø Algorithms and Data Structures
Lab 11: Pair Programming. Review: Pair Programming Roles
 Lab 11: Pair Programming Apr 2, 2019 Sprenkle - CSCI111 1 Review: Pair Programming Roles Driver (Like the role I play when we write programs in class) Uses keyboard and mouse to execute all actions on
Lab 11: Pair Programming Apr 2, 2019 Sprenkle - CSCI111 1 Review: Pair Programming Roles Driver (Like the role I play when we write programs in class) Uses keyboard and mouse to execute all actions on
Event Based Sequential Program Development: Application to Constructing a Pointer Program
 Event Based Sequential Program Development: Application to Constructing a Pointer Program Jean-Raymond Abrial Consultant, Marseille, France jr@abrial.org Abstract. In this article, I present an event approach
Event Based Sequential Program Development: Application to Constructing a Pointer Program Jean-Raymond Abrial Consultant, Marseille, France jr@abrial.org Abstract. In this article, I present an event approach
Exploring QR Factorization on GPU for Quantum Monte Carlo Simulation
 Exploring QR Factorization on GPU for Quantum Monte Carlo Simulation Tyler McDaniel Ming Wong Mentors: Ed D Azevedo, Ying Wai Li, Kwai Wong Quantum Monte Carlo Simulation Slater Determinant for N-electrons
Exploring QR Factorization on GPU for Quantum Monte Carlo Simulation Tyler McDaniel Ming Wong Mentors: Ed D Azevedo, Ying Wai Li, Kwai Wong Quantum Monte Carlo Simulation Slater Determinant for N-electrons
BMI for everyone. Compsci 6/101: PFTW. Accumulating a value. How to solve an APT. Review how APTs and Python work, run
 Compsci 6/101: PFTW Review how APTs and Python work, run Ø Good, Bad, Ugly: getting better, avoid frustration, Ø How do you run/test APT code, other Python code BMI for everyone How do we get at the data
Compsci 6/101: PFTW Review how APTs and Python work, run Ø Good, Bad, Ugly: getting better, avoid frustration, Ø How do you run/test APT code, other Python code BMI for everyone How do we get at the data
CoreLogic Matrix Terms of Use & Privacy Policy
 CoreLogic Matrix Terms of Use & Privacy Policy PLEASE READ THIS LICENSE AGREEMENT AND OUR PRIVACY POLICY (THE "AGREEMENT") CAREFULLY BEFORE YOU LOG ONTO AND/OR ACCESS THE MATRIX SYSTEM. THIS AGREEMENT
CoreLogic Matrix Terms of Use & Privacy Policy PLEASE READ THIS LICENSE AGREEMENT AND OUR PRIVACY POLICY (THE "AGREEMENT") CAREFULLY BEFORE YOU LOG ONTO AND/OR ACCESS THE MATRIX SYSTEM. THIS AGREEMENT
1. The augmented matrix for this system is " " " # (remember, I can't draw the V Ç V ß #V V Ä V ß $V V Ä V
 MATH 339, Fall 2017 Homework 1 Solutions Bear in mind that the row-reduction process is not a unique determined creature. Different people might choose to row reduce a matrix in slightly different ways.
MATH 339, Fall 2017 Homework 1 Solutions Bear in mind that the row-reduction process is not a unique determined creature. Different people might choose to row reduce a matrix in slightly different ways.
Correlations PreK, Kindergarten, First Grade, and Second Grade
 TEKS Correlations PreK, Kindergarten, First Grade, and Second Grade Skills and Activities INNOVATIVE LEARNING CONCEPTS INC. creators of TOUCHMATH TouchMath materials were first published in 1975. Innovative
TEKS Correlations PreK, Kindergarten, First Grade, and Second Grade Skills and Activities INNOVATIVE LEARNING CONCEPTS INC. creators of TOUCHMATH TouchMath materials were first published in 1975. Innovative
30 Transformational Design with Essential Aspect Decomposition: Model-Driven Architecture (MDA)
 Fakultät Informatik, Institut für Software- und Multimediatechnik, Lehrstuhl für Softwaretechnologie 30 Transformational Design with Essential Aspect Decomposition: Model-Driven Architecture () Prof. Dr.
Fakultät Informatik, Institut für Software- und Multimediatechnik, Lehrstuhl für Softwaretechnologie 30 Transformational Design with Essential Aspect Decomposition: Model-Driven Architecture () Prof. Dr.
WORLD INTELLECTUAL PROPERTY ORGANIZATION GENEVA SPECIAL UNION FOR THE INTERNATIONAL PATENT CLASSIFICATION (IPC UNION) AD HOC IPC REFORM WORKING GROUP
 WIPO IPC/REF/7/3 ORIGINAL: English DATE: May 17, 2002 WORLD INTELLECTUAL PROPERTY ORGANIZATION GENEVA E SPECIAL UNION FOR THE INTERNATIONAL PATENT CLASSIFICATION (IPC UNION) AD HOC IPC REFORM WORKING GROUP
WIPO IPC/REF/7/3 ORIGINAL: English DATE: May 17, 2002 WORLD INTELLECTUAL PROPERTY ORGANIZATION GENEVA E SPECIAL UNION FOR THE INTERNATIONAL PATENT CLASSIFICATION (IPC UNION) AD HOC IPC REFORM WORKING GROUP
DevOps Course Content
 INTRODUCTION TO DEVOPS DevOps Course Content Ø What is DevOps? Ø History of DevOps Ø Different Teams Involved Ø DevOps definitions Ø DevOps and Software Development Life Cycle o Waterfall Model o Agile
INTRODUCTION TO DEVOPS DevOps Course Content Ø What is DevOps? Ø History of DevOps Ø Different Teams Involved Ø DevOps definitions Ø DevOps and Software Development Life Cycle o Waterfall Model o Agile
Mojdeh Nikdel Patty George
 Mojdeh Nikdel Patty George Mojdeh Nikdel 2 Nearpod Ø Nearpod is an integrated teaching tool used to engage students or audience through a live, synchronized learning experience Ø Presenters use a computer
Mojdeh Nikdel Patty George Mojdeh Nikdel 2 Nearpod Ø Nearpod is an integrated teaching tool used to engage students or audience through a live, synchronized learning experience Ø Presenters use a computer
Constraint satisfaction problems. Lirong Xia
 Constraint satisfaction problems Lirong Xia Spring, 2017 Project 1 Ø You can use Windows Ø Read the instruction carefully, make sure you understand the goal search for YOUR CODE HERE Ø Ask and answer questions
Constraint satisfaction problems Lirong Xia Spring, 2017 Project 1 Ø You can use Windows Ø Read the instruction carefully, make sure you understand the goal search for YOUR CODE HERE Ø Ask and answer questions
Word of the Day Tuesday, September 4, 2018
 Tuesday, September 4, 2018 Free Trade The practice of goods being traded between countries without any (or with reduced) tariffs that might slow down trade. The practice of free trade usually results in
Tuesday, September 4, 2018 Free Trade The practice of goods being traded between countries without any (or with reduced) tariffs that might slow down trade. The practice of free trade usually results in
The Mathematics of Apportionment
 The Place: Philadelphia The Time: Summer 1787 The Players: Delegates from the 13 states The Problem: Draft a Constitution for our new nation The Big Argument: How would the people be represented? What
The Place: Philadelphia The Time: Summer 1787 The Players: Delegates from the 13 states The Problem: Draft a Constitution for our new nation The Big Argument: How would the people be represented? What
COMP : DATA STRUCTURES 2/27/14. Are binary trees satisfying two additional properties:
 BINARY HEAPS Two Additional Properties 9 Binary Heaps Are binary trees satisfying two additional properties: Ø Structure property: Levels are filled in order, left to right Also known as complete binary
BINARY HEAPS Two Additional Properties 9 Binary Heaps Are binary trees satisfying two additional properties: Ø Structure property: Levels are filled in order, left to right Also known as complete binary
Instructors: Tengyu Ma and Chris Re
 Instructors: Tengyu Ma and Chris Re cs229.stanford.edu Ø Probability (CS109 or STAT 116) Ø distribution, random variable, expectation, conditional probability, variance, density Ø Linear algebra (Math
Instructors: Tengyu Ma and Chris Re cs229.stanford.edu Ø Probability (CS109 or STAT 116) Ø distribution, random variable, expectation, conditional probability, variance, density Ø Linear algebra (Math
HPCG on Tianhe2. Yutong Lu 1,Chao Yang 2, Yunfei Du 1
 HPCG on 2 Yutong Lu 1,Chao Yang 2, Yunfei Du 1 1, Changsha, Hunan, China 2 Institute of Software, CAS, Beijing, China Outline r HPCG result overview on -2 r Key Optimization works Ø Hybrid HPCG:CPU+MIC
HPCG on 2 Yutong Lu 1,Chao Yang 2, Yunfei Du 1 1, Changsha, Hunan, China 2 Institute of Software, CAS, Beijing, China Outline r HPCG result overview on -2 r Key Optimization works Ø Hybrid HPCG:CPU+MIC
Kruskal's MST Algorithm with step-by-step execution
 Kruskal's MST Algorithm with step-by-step execution Daniel Michel Tavera Student at National Autonomous University of Mexico (UNAM) Mexico e-mail: daniel_michel@ciencias.unam.mx Social service project
Kruskal's MST Algorithm with step-by-step execution Daniel Michel Tavera Student at National Autonomous University of Mexico (UNAM) Mexico e-mail: daniel_michel@ciencias.unam.mx Social service project
MOS Exams Objective Mapping
 Core 1 Create and Manage Worksheets and Workbooks Core 1.1 Create Worksheets and Workbooks Core 1.1.1 create a workbook Level 1 Chapter 2 Topic A Core 1.1.2 import data from a delimited text file Level
Core 1 Create and Manage Worksheets and Workbooks Core 1.1 Create Worksheets and Workbooks Core 1.1.1 create a workbook Level 1 Chapter 2 Topic A Core 1.1.2 import data from a delimited text file Level
Prim's MST Algorithm with step-by-step execution
 Prim's MST Algorithm with step-by-step execution Daniel Michel Tavera Student at National Autonomous University of Mexico (UNAM) Mexico e-mail: daniel_michel@ciencias.unam.mx Social service project director:
Prim's MST Algorithm with step-by-step execution Daniel Michel Tavera Student at National Autonomous University of Mexico (UNAM) Mexico e-mail: daniel_michel@ciencias.unam.mx Social service project director:
Protocol to Check Correctness of Colorado s Risk-Limiting Tabulation Audit
 1 Public RLA Oversight Protocol Stephanie Singer and Neal McBurnett, Free & Fair Copyright Stephanie Singer and Neal McBurnett 2018 Version 1.0 One purpose of a Risk-Limiting Tabulation Audit is to improve
1 Public RLA Oversight Protocol Stephanie Singer and Neal McBurnett, Free & Fair Copyright Stephanie Singer and Neal McBurnett 2018 Version 1.0 One purpose of a Risk-Limiting Tabulation Audit is to improve
OPEN SOURCE CRYPTOCURRENCY
 23 April, 2018 OPEN SOURCE CRYPTOCURRENCY Document Filetype: PDF 325.26 KB 0 OPEN SOURCE CRYPTOCURRENCY Detailed information for OpenSourcecoin, including the OpenSourcecoin price and value, OpenSourcecoin
23 April, 2018 OPEN SOURCE CRYPTOCURRENCY Document Filetype: PDF 325.26 KB 0 OPEN SOURCE CRYPTOCURRENCY Detailed information for OpenSourcecoin, including the OpenSourcecoin price and value, OpenSourcecoin
The study of a new gerrymandering methodology
 The study of a new gerrymandering methodology arxiv:0708.2266v1 [cs.cy] 16 Aug 2007 Pan Kai, Tan Yue, and Jiang Sheng Department of Modern Physics, University of Science and Technology of China (USTC),
The study of a new gerrymandering methodology arxiv:0708.2266v1 [cs.cy] 16 Aug 2007 Pan Kai, Tan Yue, and Jiang Sheng Department of Modern Physics, University of Science and Technology of China (USTC),
RECOMMENDED CITATION: Pew Research Center, May, 2017, Partisan Identification Is Sticky, but About 10% Switched Parties Over the Past Year
 NUMBERS, FACTS AND TRENDS SHAPING THE WORLD FOR RELEASE MAY 17, 2017 FOR MEDIA OR OTHER INQUIRIES: Carroll Doherty, Director of Political Research Jocelyn Kiley, Associate Director, Research Bridget Johnson,
NUMBERS, FACTS AND TRENDS SHAPING THE WORLD FOR RELEASE MAY 17, 2017 FOR MEDIA OR OTHER INQUIRIES: Carroll Doherty, Director of Political Research Jocelyn Kiley, Associate Director, Research Bridget Johnson,
Polydisciplinary Faculty of Larache Abdelmalek Essaadi University, MOROCCO 3 Department of Mathematics and Informatics
 International Journal of Pure and Applied Mathematics Volume 115 No. 4 2017, 801-812 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: 10.12732/ijpam.v115i4.13
International Journal of Pure and Applied Mathematics Volume 115 No. 4 2017, 801-812 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: 10.12732/ijpam.v115i4.13
Title: Solving Problems by Searching AIMA: Chapter 3 (Sections 3.1, 3.2 and 3.3)
 B.Y. Choueiry 1 Instructor s notes #5 Title: Solving Problems by Searching AIMA: Chapter 3 (Sections 3.1, 3.2 and 3.3) Introduction to Artificial Intelligence CSCE 476-876, Fall 2017 URL: www.cse.unl.edu/~choueiry/f17-476-876
B.Y. Choueiry 1 Instructor s notes #5 Title: Solving Problems by Searching AIMA: Chapter 3 (Sections 3.1, 3.2 and 3.3) Introduction to Artificial Intelligence CSCE 476-876, Fall 2017 URL: www.cse.unl.edu/~choueiry/f17-476-876
Check off these skills when you feel that you have mastered them. Identify if a dictator exists in a given weighted voting system.
 Chapter Objectives Check off these skills when you feel that you have mastered them. Interpret the symbolic notation for a weighted voting system by identifying the quota, number of voters, and the number
Chapter Objectives Check off these skills when you feel that you have mastered them. Interpret the symbolic notation for a weighted voting system by identifying the quota, number of voters, and the number
TERMS AND CONDITIONS
 TERMS AND CONDITIONS Last updated 1/16/18 Effective Date 2008 BECAUSE THESE TERMS AND CONDITIONS CONTAIN LEGAL OBLIGATIONS, PLEASE READ THEM CAREFULLY BEFORE TAKING ONE OF THE PREPARE/ENRICH WEB-BASED
TERMS AND CONDITIONS Last updated 1/16/18 Effective Date 2008 BECAUSE THESE TERMS AND CONDITIONS CONTAIN LEGAL OBLIGATIONS, PLEASE READ THEM CAREFULLY BEFORE TAKING ONE OF THE PREPARE/ENRICH WEB-BASED
WEBSITE TERMS OF USE GLOBAL RESCUE S ( GR OR THE COMPANY ) INTELLECTUAL PROPERTY RIGHTS
 WEBSITE TERMS OF USE GLOBAL RESCUE S ( GR OR THE COMPANY ) INTELLECTUAL PROPERTY RIGHTS 1.1. Copyrights: All of the content of this Web site, including text, art, graphics, logos, button icons, images,
WEBSITE TERMS OF USE GLOBAL RESCUE S ( GR OR THE COMPANY ) INTELLECTUAL PROPERTY RIGHTS 1.1. Copyrights: All of the content of this Web site, including text, art, graphics, logos, button icons, images,
Hoboken Public Schools. Algebra I Curriculum
 Hoboken Public Schools Algebra I Curriculum Algebra One HOBOKEN PUBLIC SCHOOLS Course Description Algebra I reflects the New Jersey learning standards at the high school level and is designed to give students
Hoboken Public Schools Algebra I Curriculum Algebra One HOBOKEN PUBLIC SCHOOLS Course Description Algebra I reflects the New Jersey learning standards at the high school level and is designed to give students
Lecture 8: Verification and Validation
 Thanks to Prof. Steve Easterbrook University of Toronto What are goals of V&V Validation Techniques Ø Inspection Ø Model Checking Ø Prototyping Verification Techniques Ø Consistency Checking Lecture 8:
Thanks to Prof. Steve Easterbrook University of Toronto What are goals of V&V Validation Techniques Ø Inspection Ø Model Checking Ø Prototyping Verification Techniques Ø Consistency Checking Lecture 8:
TERMS OF SERVICE Effective Date: March 30 th, 2017
 TERMS OF SERVICE Effective Date: March 30 th, 2017 The following terms and conditions ( Terms of Service ) govern your access to, and use of sheshouldrun.org (the Service ) operated by She Should Run (
TERMS OF SERVICE Effective Date: March 30 th, 2017 The following terms and conditions ( Terms of Service ) govern your access to, and use of sheshouldrun.org (the Service ) operated by She Should Run (
LEGAL TERMS OF USE. Ownership of Terms of Use
 LEGAL TERMS OF USE Ownership of Terms of Use These Terms and Conditions of Use (the Terms of Use ) apply to the Compas web site located at www.compasstone.com, and all associated sites linked to www.compasstone.com
LEGAL TERMS OF USE Ownership of Terms of Use These Terms and Conditions of Use (the Terms of Use ) apply to the Compas web site located at www.compasstone.com, and all associated sites linked to www.compasstone.com
This situation where each voter is not equal in the number of votes they control is called:
 Finite Math A Chapter 2, Weighted Voting Systems 1 Discrete Mathematics Notes Chapter 2: Weighted Voting Systems The Power Game Academic Standards: PS.ED.2: Use election theory techniques to analyze election
Finite Math A Chapter 2, Weighted Voting Systems 1 Discrete Mathematics Notes Chapter 2: Weighted Voting Systems The Power Game Academic Standards: PS.ED.2: Use election theory techniques to analyze election
Probabilistic Latent Semantic Analysis Hofmann (1999)
 Probabilistic Latent Semantic Analysis Hofmann (1999) Presenter: Mercè Vintró Ricart February 8, 2016 Outline Background Topic models: What are they? Why do we use them? Latent Semantic Analysis (LSA)
Probabilistic Latent Semantic Analysis Hofmann (1999) Presenter: Mercè Vintró Ricart February 8, 2016 Outline Background Topic models: What are they? Why do we use them? Latent Semantic Analysis (LSA)
End User License Agreement for the Accenture HCM Software App
 End User License Agreement for the Accenture HCM Software App Your access to and use of this application ( Application ) is conditioned upon your acceptance of and compliance with this End User License
End User License Agreement for the Accenture HCM Software App Your access to and use of this application ( Application ) is conditioned upon your acceptance of and compliance with this End User License
A Calculus for End-to-end Statistical Service Guarantees
 A Calculus for End-to-end Statistical Service Guarantees Technical Report: University of Virginia, CS-2001-19 (2nd revised version) Almut Burchard Ý Jörg Liebeherr Stephen Patek Ý Department of Mathematics
A Calculus for End-to-end Statistical Service Guarantees Technical Report: University of Virginia, CS-2001-19 (2nd revised version) Almut Burchard Ý Jörg Liebeherr Stephen Patek Ý Department of Mathematics
Complexity of Manipulating Elections with Few Candidates
 Complexity of Manipulating Elections with Few Candidates Vincent Conitzer and Tuomas Sandholm Computer Science Department Carnegie Mellon University 5000 Forbes Avenue Pittsburgh, PA 15213 {conitzer, sandholm}@cs.cmu.edu
Complexity of Manipulating Elections with Few Candidates Vincent Conitzer and Tuomas Sandholm Computer Science Department Carnegie Mellon University 5000 Forbes Avenue Pittsburgh, PA 15213 {conitzer, sandholm}@cs.cmu.edu
Deputy Commissioner for Patent Examination Policy
 UNITED STATES PATENT AND TRADEMARK OFFICE MEMORANDUM Commissioner for Patents United States Patent and Trademark Office P.O. Box 1450 Alexandria, VA 22313-1450 www.uspto.gov Date: September 2, 2008 To:
UNITED STATES PATENT AND TRADEMARK OFFICE MEMORANDUM Commissioner for Patents United States Patent and Trademark Office P.O. Box 1450 Alexandria, VA 22313-1450 www.uspto.gov Date: September 2, 2008 To:
Coverage tools Eclipse Debugger Object-oriented Design Principles. Oct 26, 2016 Sprenkle - CSCI209 1
 Objec&ves Coverage tools Eclipse Debugger Object-oriented Design Principles Ø Design in the Small Ø DRY Ø Single responsibility principle Ø Shy Ø Open-closed principle Oct 26, 2016 Sprenkle - CSCI209 1
Objec&ves Coverage tools Eclipse Debugger Object-oriented Design Principles Ø Design in the Small Ø DRY Ø Single responsibility principle Ø Shy Ø Open-closed principle Oct 26, 2016 Sprenkle - CSCI209 1
Terms of Use. 1. Limited Use
 Terms of Use The eaccountservices.com/gmfinancialrightnotes Internet site domain name and all materials located at and under that domain name (collectively, this Site ) and any services available on this
Terms of Use The eaccountservices.com/gmfinancialrightnotes Internet site domain name and all materials located at and under that domain name (collectively, this Site ) and any services available on this
KNOWLEDGE GURU. Player s License Agreement
 KNOWLEDGE GURU Player s License Agreement Please read this entire document carefully, because it will become a binding agreement if you accept it. Bottom Line Performance Incorporated and its affiliates
KNOWLEDGE GURU Player s License Agreement Please read this entire document carefully, because it will become a binding agreement if you accept it. Bottom Line Performance Incorporated and its affiliates
NON-COMMERCIAL LICENSE AGREEMENT BETWEEN THE REGENTS OF THE UNIVERSITY OF CALIFORNIA AND LICENSEE
 NON-COMMERCIAL LICENSE AGREEMENT BETWEEN THE REGENTS OF THE UNIVERSITY OF CALIFORNIA AND LICENSEE This website (the Website ) is a service of the Rx for Change: Clinician-Assisted Tobacco Cessation Program
NON-COMMERCIAL LICENSE AGREEMENT BETWEEN THE REGENTS OF THE UNIVERSITY OF CALIFORNIA AND LICENSEE This website (the Website ) is a service of the Rx for Change: Clinician-Assisted Tobacco Cessation Program
The following list of assignments will be completed in your HISTORY NOTEBOOK. Consider them a handbook for understanding the U.S. Constitution!!!
 The following list of assignments will be completed in your HISTORY NOTEBOOK. Consider them a handbook for understanding the U.S. Constitution!!! You will be graded on the following: All required elements
The following list of assignments will be completed in your HISTORY NOTEBOOK. Consider them a handbook for understanding the U.S. Constitution!!! You will be graded on the following: All required elements
TERMS OF USE COPYRIGHT, TRADEMARK AND OTHER INTELLECTUAL PROPERTY RIGHTS
 TERMS OF USE 25 May 2018 OWNERSHIP AND AGREEMENT TO TERMS OF USE This website (the Website ) is property of SEWS CABIND S.p.A ( SEWS CABIND ). These terms (the Terms of Use ) contain important information
TERMS OF USE 25 May 2018 OWNERSHIP AND AGREEMENT TO TERMS OF USE This website (the Website ) is property of SEWS CABIND S.p.A ( SEWS CABIND ). These terms (the Terms of Use ) contain important information
Chapter. Sampling Distributions Pearson Prentice Hall. All rights reserved
 Chapter 8 Sampling Distributions 2010 Pearson Prentice Hall. All rights reserved Section 8.1 Distribution of the Sample Mean 2010 Pearson Prentice Hall. All rights reserved Objectives 1. Describe the distribution
Chapter 8 Sampling Distributions 2010 Pearson Prentice Hall. All rights reserved Section 8.1 Distribution of the Sample Mean 2010 Pearson Prentice Hall. All rights reserved Objectives 1. Describe the distribution
The 2000 U.S. presidential election was a
 aomvector/hutterstock The Geometry of Adding Up s Michael A. Jones and Jennifer Wilson The U.. presidential election was a source of interesting politics and mathematics. George W. Bush was elected president
aomvector/hutterstock The Geometry of Adding Up s Michael A. Jones and Jennifer Wilson The U.. presidential election was a source of interesting politics and mathematics. George W. Bush was elected president
Measuring a Gerrymander
 Measuring a Gerrymander Daniel Z. Levin There is no such thing as a fair or non-partisan districting plan. Whether intentionally or blindly, such plans involve political choices and have critical effects
Measuring a Gerrymander Daniel Z. Levin There is no such thing as a fair or non-partisan districting plan. Whether intentionally or blindly, such plans involve political choices and have critical effects
CORE TECHNOLOGIES CONSULTING, LLC UNLIMITED OEM SOFTWARE LICENSE AGREEMENT
 CORE TECHNOLOGIES CONSULTING, LLC UNLIMITED OEM SOFTWARE LICENSE AGREEMENT ATTENTION: PLEASE READ THIS AGREEMENT CAREFULLY BEFORE YOU INSTALL, COPY, DOWNLOAD OR USE THIS SOFTWARE ACCOMPANYING THIS PACKAGE.
CORE TECHNOLOGIES CONSULTING, LLC UNLIMITED OEM SOFTWARE LICENSE AGREEMENT ATTENTION: PLEASE READ THIS AGREEMENT CAREFULLY BEFORE YOU INSTALL, COPY, DOWNLOAD OR USE THIS SOFTWARE ACCOMPANYING THIS PACKAGE.
